Worked Example | Analysis and Design of Steel Sheet Pile Wall (EN 1997-1)

This article contains a solved example of the analysis and design of steel sheet pile walls in accordance with BS EN1997-1:2004 – Code of Practice for Geotechnical design and the UK National Annex.

Geometry
Total length of sheet pile provided H_pile = 14500 mm
Number of different types of soil N_s = 2
Retained height of soil d_ret = 3500 mm
Depth of unplanned excavation d_ex = 500 mm
Total retained height d_s = 4000 mm
Angle of retained slope β = 0.0 deg
Depth from ground level to top of water table retained side d_w = 1500 mm
Depth from ground level to top of water table retaining side;  d_wp = 4000 mm

Loading
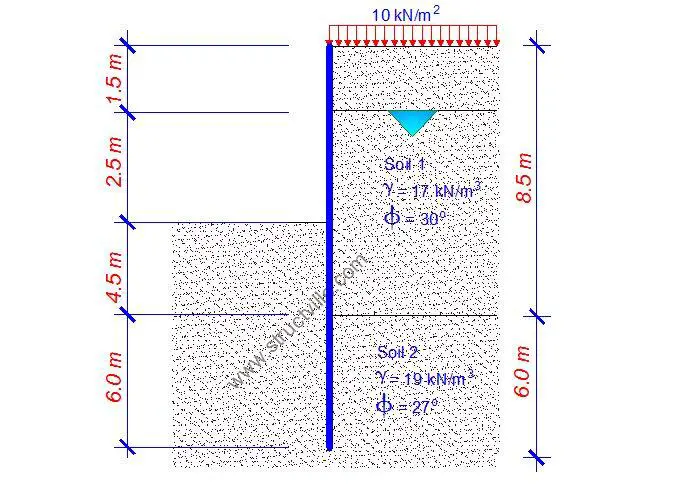
Variable surcharge p_o,Q = 10.0 kN/m²

Soil layer 1
Characteristic shearing resistance angle ϕ’_k,s1 = 30.0 deg
Characteristic wall friction angle  δ_k,s1 = 20.0 deg
Moist density of soil γ_m,s1 = 15.0 kN/m³
Characteristic saturated density of retained soil γ_s,s1 = 17.0 kN/m³
Height of soil 1  h₁ = 8500 mm

Soil layer 2
Characteristic shearing resistance angle f’_k,s2 = 27.0 deg
Characteristic wall friction angle d_k,s2 = 16.0 deg
Moist density of soil γ_m,s2 = 16.0 kN/m³
Characteristic saturated density of retained soil γ_s,s2 = 19.0 kN/m³
Height of soil 2 h₂ = 7000 mm

Partial factors on actions – Section A.3.1 – Combination 1
Permanent unfavourable action γ_G = 1.35
Permanent favourable action γ_G,f = 1.00
Variable unfavourable action γ_Q = 1.50
Angle of shearing resistance γ_ϕ’ = 1.00
Weight density γ_g = 1.00

Design soil properties – soil 1
Design effective shearing resistance angle ϕ’_d = tan^-1[tan(ϕ’_k)/γ_ϕ’] = 30.0 deg
Design wall friction angle  δ_d = tan^-1[tan(ϕ_k)/γ_ϕ’] = 20.0 deg
Design moist density of retained soil γ_m.d1 = γ_m/γ_γ = 15.0 kN/m³
Design saturated density of retained soil γ_s.d1 = γ_s/γ_γ = 17.0 kN/m³
Design buoyant density of retained soil γ_d.d1 = γ_s.d1 – γ_w = 7.2 kN/m³

Active pressure using Coulomb theory K_a1 = sin(α + ϕ’_d)² / (sin(α)² × sin(α – δ_d) × (1 + √(sin(ϕ’_d + δ_d) × sin(ϕ’_d – β)/(sin(α – δ_d) × sin(α + β))))²) = 0.297

Passive pressure using Coulomb theory K_p1 = sin(90 – ϕ’_d)² / (sin(90 + δ_d) × [1 – √[sin(ϕ’_d + δ_d) × sin(ϕ’_d) / (sin(90 + δ_d))]]²) = 6.105

Design soil properties – soil 2
Design effective shearing resistance angle ϕ’_d = tan^-1(tan(ϕ’_k) /γ_ϕ’) = 27.0 deg
Design wall friction angle  δ_d = tan_-1(tan(δ_k)/γ_ϕ’) = 16.0 deg
Design moist density of retained soil γ_m.d2 = γ_m/γ_γ = 16.0 kN/m³
Design saturated density of retained soil γ_s.d2 = γ_s /γ_γ = 19.0 kN/m³
Design buoyant density of retained soil γ_d.d2 = γ_s.d2 – γ_w = 9.2 kN/m³

Active pressure using Coulomb theory K_a2 = sin(α + ϕ’_d)² / (sin(α)² × sin(α – δ_d) × (1 + √(sin(ϕ’_d + δ_d) × sin(ϕ’_d – β) / (sin(α – δ_d) × sin(α + β))))²) = 0.336

Passive pressure using Coulomb theory K_p2 = sin(90 – ϕ’_d)² / (sin(90 + δ_d) × [1 – √[sin(ϕ’_d + δ_d) × sin(ϕ’_d) / (sin(90 + δ_d))]]²) = 4.416

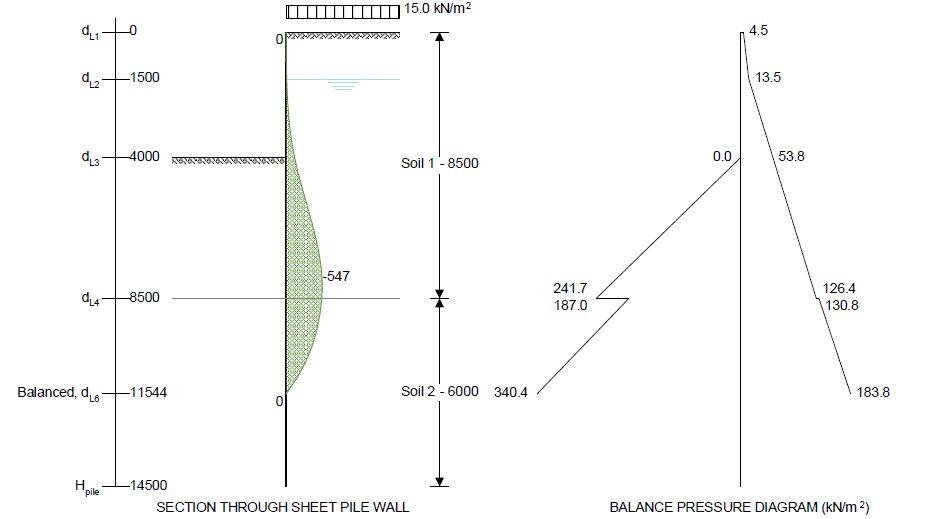
Overburden on the active side
Overburden at 0 mm below GL in soil 1; OB’_a11 = p_o,Q × γ_Q = 15.0 kN/m²
Overburden at 1500 mm below GL in soil 1; OB’_a21 = γ_G × γ_m.d1 × h_a1 + OB’_a11 = 45.4 kN/m²
Overburden at 4000 mm below GL in soil 1; OB’_a31 = γ_G × γ_d.d1 × h_a2 + OB’_a21 = 69.6 kN/m²
Overburden at 8500 mm below GL in soil 1; OB’_a41 = γ_G × γ_d.d1 × h_a3 + OB’_a31 = 113.3 kN/m²
Overburden at 8500 mm below GL in soil 2; OB’_a42 = γ_G × γ_d.d1 × h_a3 + OB’_a31 = 113.3 kN/m²
Overburden at 11544 mm below GL in soil 2; OB’_a51 = γ_G × γ_d.d2 × h_a4 + OB’_a42 = 151.1 kN/m²

Overburden on the passive side
Overburden at 4000 mm below GL in soil 1; OB’_p31 = 0 kN/m² = 0.0 kN/m²
Overburden at 8500 mm below GL in soil 1; OB’_p41 = γ_G,f × γ_d.d1 × h_p3 + OB’_p31 = 32.4 kN/m²
Overburden at 8500 mm below GL in soil 2; OB’_p42 = γ_G,f × γ_d.d1 × h_p3 + OB’_p31 = 32.4 kN/m²
Overburden at 11544 mm below GL in soil 2; OB’_p51 = γ_G,f × γ_d.d2 × h_p4 + OB’_p42 = 60.3 kN/m²

Pressure on the active side
Active at 0 mm below GL in soil 1; p’_a11 = K_a1 × OB’_a11 = 4.5 kN/m²
Active at 1500 mm below GL in soil 1; p’_a21 = K_a1 × OB’_a21 = 13.5 kN/m²
Active at 4000 mm below GL in soil 1; p’_a31 = K_a1 × OB’_a31 + γ_γ × γ_w × (d_L3 – d_w) = 53.8 kN/m²
Active at 8500 mm below GL in soil 1; p’_a41 = K_a1 × OB’_a41 + γ_γ × γ_w × (d_L4 – d_w) = 126.4 kN/m²
Active at 8500 mm below GL in soil 2; p’_a42 = K_a2 × OB’_a42 + γ_γ × γ_w × (d_L4 – d_w) = 130.8 kN/m²
Active at 11544 mm below GL in soil 2; p’_a51 = K_a2 × OB’_a51 + γ_γ × γ_w × (d_L5 – d_w) = 183.8 kN/m²

Pressure on the passive side
Passive at 4000 mm below GL in soil 1; p’_p31 = K_p1 × OB’_p31 + γ_G,f × γ_w × (d_L3 – max(d_s, d_w)) = 0.0 kN/m²
Passive at 8500 mm below GL in soil 1; p’_p41 = K_p1 × OB’_p41 + γ_G,f × γ_w × (d_L4 – max(d_s, d_w)) = 241.7 kN/m²
Passive at 8500 mm below GL in soil 2; p’_p42 = K_p2 × OB’_p42 + γ_G,f × γ_w × (d_L4 – max(d_s, d_w)) = 187.0 kN/m²
Passive at 11544 mm below GL in soil 2; p’_p51 = K_p2 × OB’_p51 + γ_G,f × γ_w × (d_L5 – max(d_s, d_w)) = 340.4 kN/m²

By iteration the depth at which the active moments equal the passive moments has been determined as 11544 mm as follows:-

Active moment about 11544 mm

Moment level 1;M_a11 = 0.5 × p’_a11 × h_a1 × ((H – d_L2) + 2/3 × h_a1) = 36.9 kNm/m
Moment level 1; M_a12 = 0.5 × p’_a21 × h_a1 × ((H – d_L2) + 1/3 × h_a1) = 106.7 kNm/m
Moment level 2; M_a21 = 0.5 × p’_a21 × h_a2 × ((H – d_L3) + 2/3 × h_a2) = 155.3 kNm/m
Moment level 2; M_a22 = 0.5 × p’_a31 × h_a2 × ((H – d_L3) + 1/3 × h_a2) = 563.5 kNm/m
Moment level 3; M_a31 = 0.5 × p’_a31 × h_a3 × ((H – d_L4) + 2/3 × h_a3) = 731.8 kNm/m
Moment level 3; M_a32 = 0.5 × p’_a41 × h_a3 × ((H – d_L4) + 1/3 × h_a3) = 1292.3 kNm/m
Moment level 4; M_a41 = 0.5 × p’_a42 × h_a4 × ((H – d_L5) + 2/3 × h_a4) = 404.0 kNm/m
Moment level 4; M_a42 = 0.5 × p’_a51 × h_a4 × ((H – d_L5) + 1/3 × h_a4) = 283.8 kNm/m

Passive moment about 11544 mm

Moment level 3; M_p31 = 0.5 × p’_p31 × h_p3 × ((H – d_L4) + 2/3 × h_p3) = 0.0 kNm/m
Moment level 3; M_p32 = 0.5 × p’_p41 × h_p3 × ((H – d_L4) + 1/3 × h_p3) = 2471.0 kNm/m
Moment level 4; M_p41 = 0.5 × p’_p42 × h_p4 × ((H – d_L5) + 2/3 × h_p4) = 577.6 kNm/m
Moment level 4; M_p42 = 0.5 × p’_p51 × h_p4 × ((H – d_L5) + 1/3 × h_p4) = 525.7 kNm/m

Total moments about 11544 mm

Total active moment; SM_a = 3574.5 kNm/m
Total passive moment; SM_p = 3574.5 kNm/m

Required pile length
Length of pile required to balance moments; H = 11544 mm

Depth of equal pressure; d_contra = 5432 mm
Add 20% below this point; d_{e_add} = 1.2 × (H – d_contra) = 7334 mm

Minimum required pile length; H_total = d_contra + d_{e_add} = 12766 mm

Pass – Provided length of sheet pile greater than the minimum required length of the pile

Pile capacity (EN1993-5)
Maximum moment in pile (from analysis); M_pile = max(abs(M_min), abs(M_max)) / 1m = 547.0 kNm/m
Maximum shear force in pile (from analysis); V_pile = 364.7 kN/m
Nominal yield strength of pile; f_{y_pile} = 355 N/mm²
Name of sheet pile;  Arcelor PU(18)
Classification of pile; 2
Plastic modulus of pile; W_pl.y = 2134 cm³/m

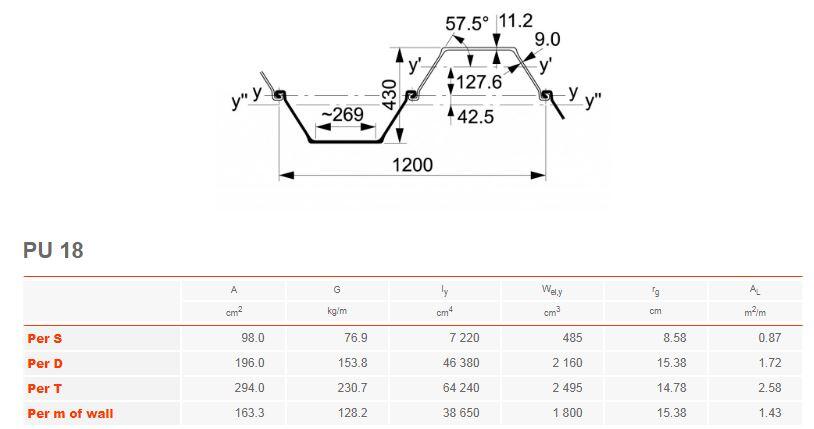
Shear buckling of web (cl.5.2.2(6))
Width of section; c = h / sin(α_pile) = 510 mm
Thickness of web;  t_w = s = 9.0 mm
ε = √(235/f_{y_pile}) = 0.814
c/t_w = 56.6 = 69.6ε < 72ε
PASS – Shear buckling of web within limits

Bending 2
Interlock reduction factor (cl.5.2.2); β_B = 1
Design bending resistance (eqn.5.2);                         
M_c,Rd = W_pl.y × f_{y_pile} × β_B / γ_M0 = 757.6 kNm/m
PASS – Moment capacity exceeds moment in pile

Shear
Projected shear area of web (eqn.5.6); A_v = s × (h – t) = 3769 mm²
Design shear resistance (eqn.5.5); V_pl,Rd = A_v × f_{y_pile} / (√(3) × γ_M0) / b = 1287.6 kN/m
PASS – Shear capacity exceeds shear in pile

Partial factors on actions – Section A.3.1 – Combination 2

Permanent unfavourable action;  γ_G = 1.00
Permanent favourable action; γ_G,f = 1.00
Variable unfavourable action; γ_Q = 1.30
Angle of shearing resistance; γ_ϕ’ = 1.25
Weight density; γ_γ = 1.00

Design soil properties – soil 1
Design effective shearing resistance angle; ϕ’_d = tan^-1(tan(ϕ’_k)/γ_ϕ’) = 24.8 deg
Design wall friction angle;  δ_d = tan^-1(tan(δ_k)/γ_ϕ’) = 16.2 deg
Design moist density of retained soil; γ_m.d1 = γ_m/γ_γ = 15.0 kN/m³
Design saturated density of retained soil; γ_s.d1 = γ_s/γ_γ = 17.0 kN/m³
Design buoyant density of retained soil; γ_d.d1 = γ_s.d1 – γ_w = 7.2 kN/m³

Active pressure using Coulomb theory; K_a1 = sin(α + ϕ’_d)² / (sin(α)² × sin(α – δ_d) × (1 + √(sin(ϕ’_d + δ_d) × sin(ϕ’_d – β)/(sin(α – δ_d) ´ sin(α + β))))²) = 0.364

Passive pressure using Coulomb theory; K_p1 = sin(90 – ϕ’_d)² / (sin(90 + δ_d) × [1 – √[sin(ϕ’_d + δ_d) × sin(ϕ’_d) / (sin(90 + δ_d))]]²) = 3.977

Design soil properties – soil 2

Design effective shearing resistance angle; ϕ’_d2 = tan^-1(tan(ϕ’_k)/γ_ϕ’) = 22.2 deg
Design wall friction angle; δ_d2 = tan^-1(tan(δ_k)/γ_ϕ’) = 12.9 deg
Design moist density of retained soil; γ_m.d2 = γ_m/γ_γ = 16.0 kN/m³
Design saturated density of retained soil; γ_s.d2 = γ_s/γ_γ = 19.0 kN/m³
Design buoyant density of retained soil; γ_d.d2 = γ_s.d2 – γ_w = 9.2 kN/m³

Active pressure using Coulomb theory; K_a2 = sin(α + ϕ’_d)² / (sin(α)² × sin(α – δ_d) × (1 + √(sin(ϕ’_d + δ_d) × sin(ϕ’_d – β) / (sin(α – δ_d) × sin(α + β))))²) = 0.406

Passive pressure using Coulomb theory; K_p2 = sin(90 – ϕ’_d)² / (sin(90 + δ_d) × [1 – √[sin(ϕ’_d + δ_d) × sin(f’_d) / (sin(90 + δ_d))]]²) = 3.154

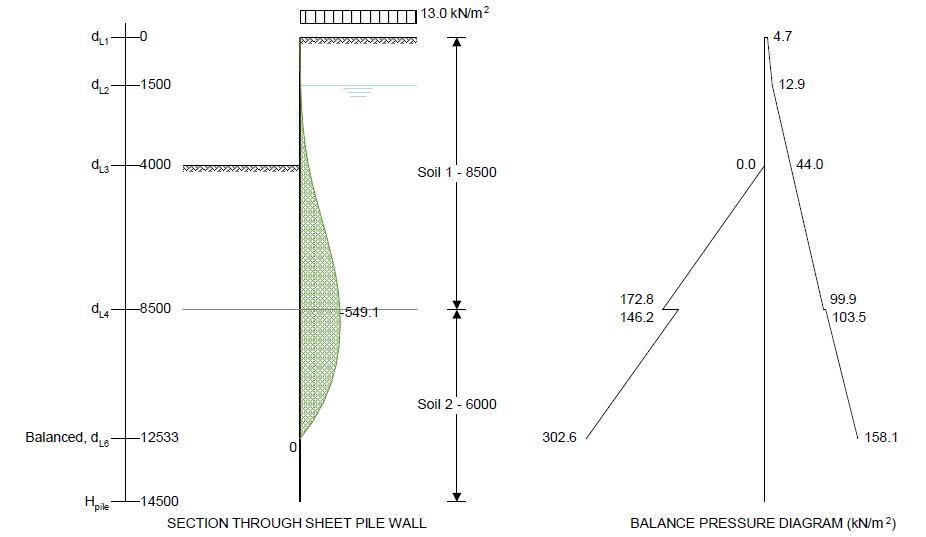
Overburden on the active side
Overburden at 0 mm below GL in soil 1; OB’_a11 = p_o,Q × γ_Q = 13.0 kN/m²
Overburden at 1500 mm below GL in soil 1;  OB’_a21 = γ_G × γ_m.d1 × h_a1 + OB’_a11 = 35.5 kN/m²
Overburden at 4000 mm below GL in soil 1; OB’_a31 = γ_G × γ_d.d1 × h_a2 + OB’_a21 = 53.5 kN/m²
Overburden at 8500 mm below GL in soil 1; OB’_a41 = γ_G × γ_d.d1 × h_a3 + OB’_a31 = 85.8 kN/m²
Overburden at 8500 mm below GL in soil 2; OB’_a42 = γ_G × γ_d.d1 × h_a3 + OB’_a31 = 85.8 kN/m²
Overburden at 12532 mm below GL in soil 2;OB’_a51 = γ_G × γ_d.d2 × h_a4 + OB’_a42 = 122.9 kN/m²

Overburden on the passive side
Overburden at 4000 mm below GL in soil 1; OB’_p31 = 0 kN/m² = 0.0 kN/m²
Overburden at 8500 mm below GL in soil 1; OB’_p41 = γ_G,f × γ_d.d1 × h_p3 + OB’_p31 = 32.4 kN/m²
Overburden at 8500 mm below GL in soil 2; OB’_p42 = γ_G,f × γ_d.d1 × h_p3 + OB’_p31 = 32.4 kN/m²
Overburden at 12532 mm below GL in soil 2;OB’_p51 = γ_G,f × γ_d.d2 × h_p4 + OB’_p42 = 69.4 kN/m²

Pressure on the active side

Active at 0 mm below GL in soil 1; p’_a11 = K_a1 × OB’_a11 = 4.7 kN/m²
Active at 1500 mm below GL in soil 1; p’_a21 = K_a1 × OB’_a21 = 12.9 kN/m²
Active at 4000 mm below GL in soil 1; p’_a31 = K_a1 × OB’_a31 + γ_G × γ_w × (d_L3 – d_w) = 44.0 kN/m²
Active at 8500 mm below GL in soil 1; p’_a41 = K_a1 × OB’_a41 + γ_G × γ_w × (d_L4 – d_w) = 99.9 kN/m²
Active at 8500 mm below GL in soil 2; p’_a42 = K_a2 × OB’_a42 + γ_G × γ_w × (d_L4 – d_w) = 103.5 kN/m²
Active at 12532 mm below GL in soil 2; p’_a51 = K_a2 × OB’_a51 + γ_G × γ_w × (d_L5 – d_w) = 158.1 kN/m²

Pressure on the passive side

Passive at 4000 mm below GL in soil 1; p’_p31 = K_p1 × OB’_p31 + γ_G,f × γ_w × (d_L3 – max(d_s, d_w)) = 0.0 kN/m²
Passive at 8500 mm below GL in soil 1; p’_p41 = K_p1 × OB’_p41 + γ_G,f × γ_w × (d_L4 – max(d_s, d_w)) = 172.8 kN/m²
Passive at 8500 mm below GL in soil 2;p’_p42 = K_p2 × OB’_p42 + γ_G,f × γ_w × (d_L4 – max(d_s, d_w)) = 146.2 kN/m²
Passive at 12532 mm below GL in soil 2; p’_p51 = K_p2 × OB’_p51 + γ_G,f × γ_w × (d_L5 – max(d_s, d_w)) = 302.7 kN/m²

By iteration the depth at which the active moments equal the passive moments has been determined as 12533 mm as follows:-

Active moment about 12533 mm

Moment level 1; M_a11 = 0.5 × p’_a11 × h_a1 × ((H – d_L2) + 2/3 × h_a1) = 42.7 kNm/m
Moment level 1; M_a12 = 0.5 × p’_a21 × h_a1 × ((H – d_L2) + 1/3 × h_a1) = 111.8 kNm/m
Moment level 2; M_a21 = 0.5 × p’_a21 × h_a2 × ((H – d_L3) + 2/3 × h_a2) = 164.8 kNm/m
Moment level 2; M_a22 = 0.5 × p’_a31 × h_a2 × ((H – d_L3) + 1/3 × h_a2) = 515.1 kNm/m
Moment level 3; M_a31 = 0.5 × p’_a31 × h_a3 × ((H – d_L4) + 2/3 × h_a3) = 696.2 kNm/m
Moment level 3; M_a32 = 0.5 × p’_a41 × h_a3 × ((H – d_L4) + 1/3 × h_a3) = 1244.0 kNm/m
Moment level 4; M_a41 = 0.5 × p’_a42 × h_a4 × ((H – d_L5) + 2/3 × h_a4) = 561.3 kNm/m
Moment level 4; M_a42 = 0.5 × p’_a51 × h_a4 × ((H – d_L5) + 1/3 × h_a4) = 428.7 kNm/m

Passive moment about 12533 mm

Moment level 3; M_p31 = 0.5 × p’_p31 × h_p3 × ((H – d_L4) + 2/3 × h_p3) = 0.0 kNm/m
Moment level 3; M_p32 = 0.5 × p’_p41 × h_p3 × ((H – d_L4) + 1/3 × h_p3) = 2151.5 kNm/m
Moment level 4; M_p41 = 0.5 × p’_p42 × h_p4 × ((H – d_L5) + 2/3 × h_p4) = 792.7 kNm/m
Moment level 4; M_p42 = 0.5 × p’_p51 × h_p4 × ((H – d_L5) + 1/3 × h_p4) = 820.5 kNm/m

Total moments about 12533 mm

Total active moment; SM_a = 3763.9 kNm/m
Total passive moment; SM_p = 3763.7 kNm/m

Required pile length
Length of pile required to balance moments; H = 12533 mm

Depth of equal pressure; d_contra = 5694 mm
Add 20% below this point; d_{e_add} = 1.2 × (H – d_contra) = 8207 mm
Minimum required pile length; H_total = d_contra + d_{e_add} = 13901 mm

PASS – Provided length of sheet pile greater than the minimum required length of pile

Pile capacity (EN1993-5)

Maximum moment in pile (from analysis); M_pile = max(abs(M_min), abs(M_max)) / 1m = 549.1 kNm/m
Maximum shear force in pile (from analysis); V_pile = 358.1 kN/m
Nominal yield strength of pile; f_{y_pile} = 355 N/mm²
Name of pile;  Arcelor PU(18)
Classification of pile; 2
Plastic modulus of pile; W_pl.y = 2134 cm³/m

Shear buckling of web (cl.5.2.2(6))

Width of section; c = h / sin(a_pile) = 510 mm
Thickness of web; t_w = s = 9.0 mm
ε = √(235/f_{y_pile})= 0.814
c / t_w = 56.6 = 69.6ε < 72ε

PASS – Shear buckling of web within limits

Bending
Interlock reduction factor (cl.5.2.2); β_B = 1
Design bending resistance (eqn.5.2);M_c,Rd = W_pl.y × f_{y_pile} × β_B / γ_M0 = 757.6 kNm/m

PASS – Moment capacity exceeds moment in pile

Shear
Projected shear area of web (eqn.5.6); A_v = s × (h – t) = 3769 mm²
Design shear resistance (eqn.5.5); V_pl,Rd = A_v × f_{y_pile} / (√(3) × γ_M0) / b = 1287.6 kN/m

PASS – Shear capacity exceeds shear in the pile

To obtain this article in PDF format, click HERE (premium, but very affordable).