Worked Example | Design of RC beams for Torsion (EN 1992-1:2004)

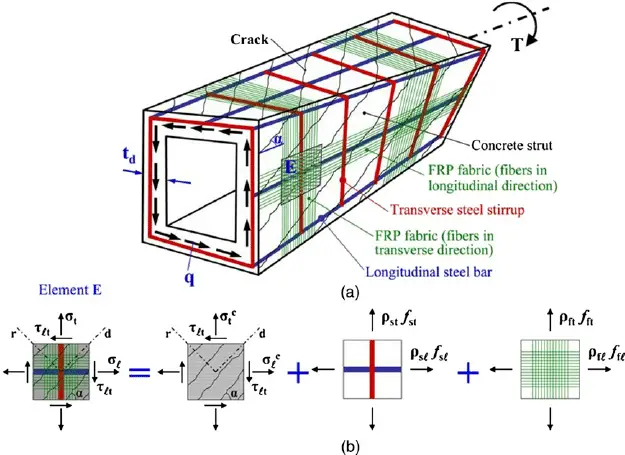
A full torsional design covering the ultimate and serviceability limit states is required when the equilibrium of a structure is dependent on the torsional resistance of the member. Reinforced concrete (RC) beams are subjected to torsion when the point of application of loads does not coincide with the shear centre of the beams. This can be due to the arrangement of the beams or the loading pattern as can be found in circular or canopy beams.

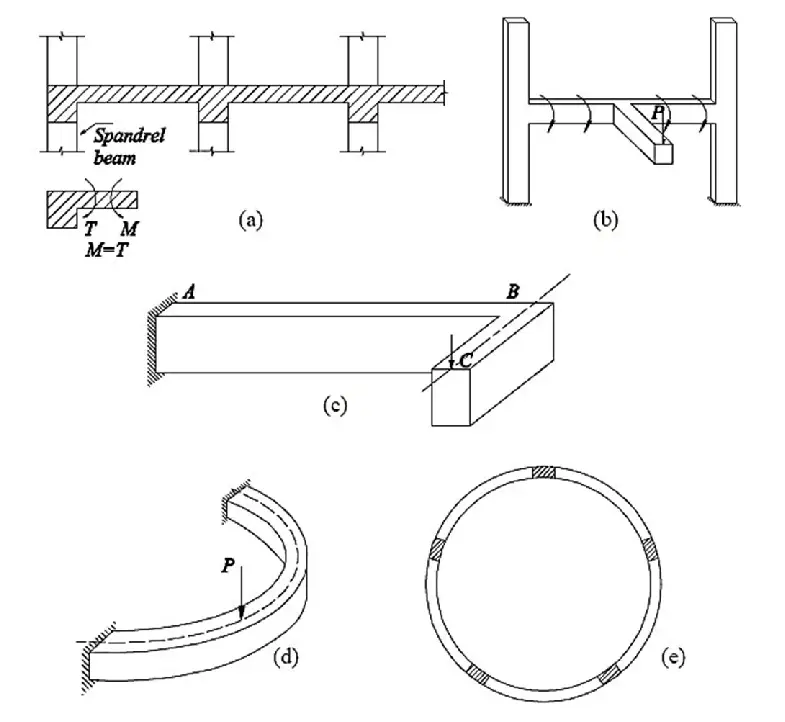
According to clause 6.3.1(3) of EN 1992-1:2004, the torsional resistance of a section may be calculated on the basis of a thin-walled closed section, in which equilibrium is satisfied by a closed shear flow. Solid sections may be modelled by equivalent thin-walled sections. Complex shapes, such as T-sections, may be divided into a series of sub-sections, each of which is modelled as an equivalent thin-walled section, and the total torsional resistance taken as the sum of the capacities of the individual elements.

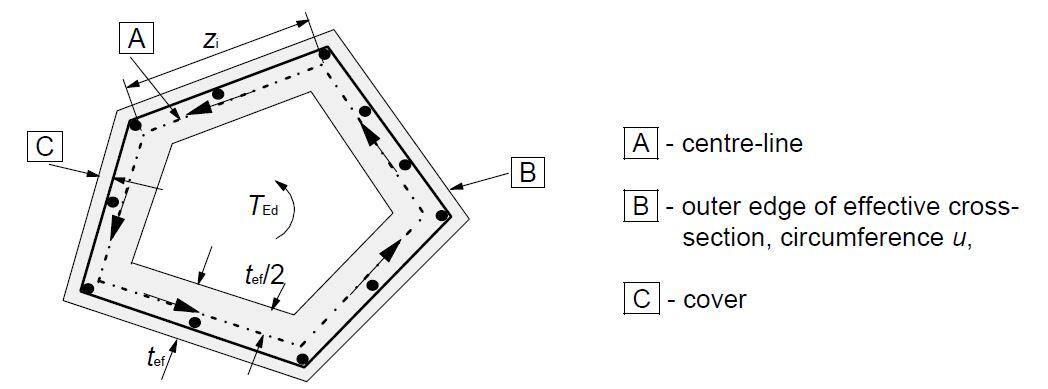
In Eurocode 2, the shear stress in a wall of a section subject to a pure torsional moment may be calculated from:

τ_t,it_ef,i = T_Ed/2A_k

The shear force V_Ed,i in a wall i due to torsion is given by:

V_Ed,i = τ_t,it_ef,izi

where;
T_Ed is the applied design torsion
A_k is the area enclosed by the centre-lines of the connecting walls, including inner hollow areas.
τ_t,i is the torsional shear stress in wall i
t_ef,i is the effective wall thickness. It may be taken as A/u, but should not be taken as less than twice the distance between edge and centre of the longitudinal reinforcement. For hollow sections the real thickness is an upper limit
A is the total area of the cross-section within the outer circumference, including inner hollow areas
u is the outer circumference of the cross-section
z_i is the side length of wall i defined by the distance between the intersection points with the adjacent walls

The required cross-sectional area of the longitudinal reinforcement for torsion ΣA_sl may be calculated from Expression (6.28) of EC2:

ΣA_sl/f_yd = T_Edcotθ/2A_k

where;
u_k is the perimeter of the area A_k
f_yd is the design yield stress of the longitudinal reinforcement A_sl
θ is the angle of compression struts

According to clause 6.3.2(4) of EC2, the maximum resistance of a member subjected to torsion and shear is limited by the capacity of the concrete struts. In order not to exceed this resistance the following condition should be satisfied:

T_Ed/T_Rd,max + V_Ed/V_Rd,max ≤ 1.0 (Equation 6.29, EC2)

where:
T_Ed is the design torsional moment
V_Ed is the design transverse force
T_Rd,max is the design torsional resistance moment = T_Rd,max = 2να_cwf_cdA_kt_ef,isinθcosθ
V_Rd,max is the maximum design shear resistance according to Expressions (6.9) of EC2

Worked Example

Carry out a full torsional design of a rectangular reinforced concrete (RC) beam subjected to an ultimate torsional moment of 55 kNm, and shear force of 225 kN. The section is 600 x 400 mm, and reinforcement of 4H25 (A_s,prov = 1964 mm²) has been provided to resist the bending moment. (f_ck = 28 N/mm²; f_yk = 500 N/mm²)

Solution

Concrete strength class; C28/35 ×γα
Characteristic compressive cylinder strength;f_ck = 28 N/mm²
Partial factor for concrete -Table 2.1N; γ_C = 1.50
Compression chord stress coefficient – cl.6.2.3(3); α_cw = 1.00
Compressive strength coefficient – cl.3.1.6(1); α_cc = 0.85
Design compressive concrete strength – exp.3.15;   f_cd = α_cc × f_ck/γ_C = 15.9 N/mm²
Compressive strength coefficient – cl.3.1.6(1); α_ccw = 1.00
Design compressive concrete strength – exp.3.15;   f_cwd = α_ccw × f_ck/γ_C = 18.7 N/mm²
Tensile strength coefficient – cl.3.1.6(2); α_ct = 1.00
Mean value of axial strength of conc. – cl.3.1.6(2);    f_ctm = 0.3 N/mm² × (f_ck)^2/3 = 2.77 N/mm²

Characteristic axial strength of conc. (5% factile);    f_ctk,0.05 = 0.7 × f_ctm = 1.94 N/mm²
Design axial strength of concrete; f_ct,d = a_ct × f_ctk,0.05/γ_C = 1.29 N/mm²

Reinforcement details
Characteristic yield strength of reinforcement; f_yk = 500 N/mm²
Partial factor for reinforcing steel – Table 2.1N; γ_S = 1.15
Design yield strength of reinforcement;  f_yd = f_yk/γ_S = 435 N/mm²

Beam dimensions
Section width; b = 400 mm
Section depth; h = 600 mm

Design forces
Maximum design torsional moment; T_Ed,max = 55.0 kNm
Maximum design shear force; V_Ed,max = 225.0 kN
Area of design longitudinal reinforcement; A_sl = 1964 mm²
Effective depth to outer layer; d = 450 mm

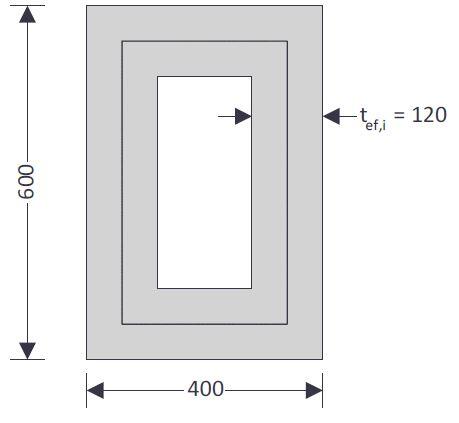
Torsional resistance (Section 6.3, EC2)

Effective thickness of walls – cl.6.3.2(1); t_ef,i = (b × h) / (2 × (b + h)) = 120 mm
Area enclosed by centre lines of walls – cl.6.3.2(1);  A_k = (b – t_ef,i) × (h – t_ef,i) = 134400 mm²
Perimeter – cl.6.3.2(3); U_k = 2 × ((b – t_ef,i) + (h – t_ef,i)) = 1520 mm

Strength reduction factor;  v₁ = 0.6 × (1 – f_ck / 250 N/mm²) = 0.533

Design shear stress; v_t,Ed = V_Ed,max / (b × d) = 1.250 N/mm²

Torsional shear stress in wall – exp.6.26;  t_t,Ed = T_Ed,max / (2 × A_k × t_ef,i) = 1.705 N/mm²

Concrete strut angle;q_t = min[45°, max(0.5 × Asin(min(2 × (v_t,Ed / 0.9 + t_t,Ed) / (α_cw × f_cwd × v₁), 1)), 21.8°)] = 21.8°

Max design value of torsional resist. mnt – exp 6.30; T_Rd,max = 2 × v₁ × α_cw × f_cd × A_k × t_ef,i × sin(q_t) × cos(q_t) = 94.0 kNm

Max design shear force – exp.6.9; V_Rdt,max = a_cw × b × 0.9 × d × v₁ × f_cwd / (cot(q_t) + tan(q_t)) = 555.6 kN

Interaction formulae – exp.6.29; T_Ed,max / T_Rd,max + V_Ed,max / V_Rdt,max = 0.990

PASS – concrete section is adequate

Torsional and shear resistance of the concrete alone

Maximum torsional resist moment with no shear reinf. – cl.6.3.2(5);  T_Rd,c = 2 × A_k × f_ct,d × t_ef,i = 41.6 kNm
Shear resistance constant – cl.6.2.2; C_Rd,c = 0.18/γ_C = 0.120
Reinforcement ratio – cl.6.2.2; r_l = min(A_sl/(d × b), 0.02) = 0.011
Effective depth factor – cl.6.2.2; k_v = min(1 + √(200mm/d), 2) = 1.667

Minimum shear stress; v_min = 0.035 N/mm² × k_v^3/2 × (f_ck / 1N/mm²)^0.5 = 0.4 N/mm²

Design value for shear resistance – exp.6.2.a;   V_Rd,c = max(C_Rd,c × k_v × 1N/mm² × (100 × r_l × f_ck/1N/mm²)^1/3 × b × d, v_min × b × d) = 112.5 kN

Interaction formulae – exp.6.31; T_Ed,max / T_Rd,c + V_Ed,max / V_Rd,c = 3.320
Therefore, additional reinforcement required

Required torsional reinforcement
Required area of add. long. reinf. for torsion (6.28); A_sl,req = T_Ed,max × U_k × cot(q_t) / (2 × A_k × f_yd) = 1788 mm²
Provide 10Y16 side bars (5 on each face) for torsion (Asprov = 2010 mm²)

The longitudinal bars should be arranged so there is at least one bar at each corner with the other spaced around the periphery of the links at a spacing of 350mm or less (cl.9.2.3(4))

Required shear reinforcement for torsion (one leg); A_sw,req = T_Ed,max / (2 × A_k × f_yd × cot(q_t)) = 188 mm²/m
Maximum spacing for torsion shear reinforcement;  s_w,max = min(U_k/8, b, h) = 190 mm

Provide 2 legs H10@175 c/c as torsion/shear reinforcement

[Featured Image Credit] Chai H.K., Majeed A.A., Allawi A.A (2015): Torsional Analysis of Multicell Concrete Box Girders Strengthened with CFRP Using a Modified Softened Truss Model. ASCE Journal of Bridge Engineering, 20(8) https://doi.org/10.1061/(ASCE)BE.1943-5592.0000621

To download this article in PDF format, click HERE