Effect of Groundwater Table on the Bearing Capacity of Shallow Foundations

Bearing capacity is the maximum load a soil profile can withstand before undergoing excessive deformation and final shear failure. It is well understood that the depth of the groundwater table can affect the strength of soils, but a high water table does not necessarily indicate that the soil is weak as sometimes misunderstood. However, the presence of groundwater in soils can reduce the strength due to the way water affects the unit weight of soils and the shear strength parameters – cohesion (c) and angle of internal friction (ϕ).

If we consider Terzaghi’s general bearing capacity equation;

q_ult = cN_c + γD_fN_q + 0.5γbN_γ —— (1)

We will discover that the equation contains terms for cohesion (c), angle of internal friction (ϕ), and unit weight of the soil (γ). The bearing capacity factors N_c, N_q, and N_γ depend on the angle of internal friction. When the soil is submerged, the effective unit weight (γ′) is to be used in the computation of bearing capacity.

γ′ = γ_sat – γ_w —— (2)

Where;
γ′ = Effective unit weight of the soil
γ_sat = saturated unit weight of the soil
γ_w = Where is the unit weight of water

As can be seen from Equation (2), the effective unit weight γ′ is about half the saturated unit weight; consequently, there will be about 50% reduction in the value of the corresponding term in the bearing capacity formula. Similarly, the effective stress parameters, c′ and φ′, obtained from an appropriate test in the laboratory, on a saturated sample of the soil, are to be used. It should be noted that water also affects the shear strength parameters c′ and φ′ but their effects are usually so small that they are ignored.

It should be now obvious that the location of the groundwater table and its seasonal fluctuations have an effect on the bearing capacity of a foundation. If the water table is at a great depth from the base of the foundation, there will be no effect or reduction in the bearing capacity.

In the design of footings, the minimum depth below the base of the footing at which the water table is not expected to have an effect on the bearing capacity is set at a value equal to the width of the footing. This is because the maximum depth of the zone of shear failure below the base is not expected to exceed this value ordinarily.

However, if the water table is above this level, there will be a reduction in the bearing capacity. If the water table is at the level of the base of the footing, γ′ is to be used for γ in the third term, which indicates the contribution of the weight of the soil in the elastic wedge beneath the base of the footing, since the entire wedge is submerged.

Therefore, three cases are usually considered in the design of footings for the effect of the water table;

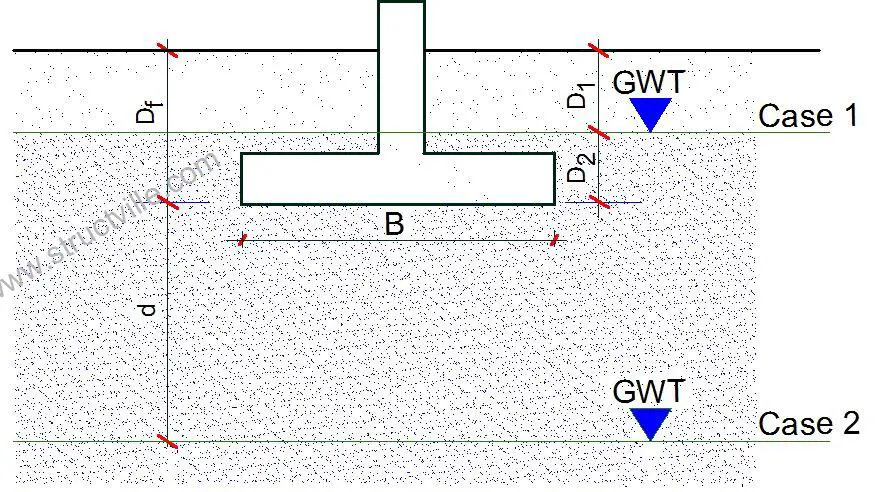
Case 1: If the water table is located so that 0 ≤ D₁ ≤ D_f (water table above the footing level), the factor q in the bearing capacity equations takes the form;
q = effective surcharge = D₁γ + D₂(γ_sat – γ_w)

Case 2: If the water table is located so that 0 ≤ d ≤ B (water table at footing level or within the depth d), the factor q in the bearing capacity equations takes the form;
q = effective surcharge = γD_f

The factor γ in the last term of the bearing capacity equation will have to be replaced by the factor;

ỹ = γ’ + d/B(γ – γ’)

Case 3: When the water table is located such that d ≥ B, the water table will have no effect on the bearing capacity.

Worked Example on Effect of Groundwater Table

A footing 2 m square, subjected to a centric vertical load, is located at a depth of 1.0 m below the ground surface in a deep deposit of compacted sand, φ′ = 30°, and γ_sat = 19 kN/m³. Determine the allowable bearing capacity using Terzaghi’s theory when the water table is at;

(a) at 5m below the ground surface
(b) at the ground surface
(c) at the bottom of the base of the footing, and
(d) at 1 m below the base

Solution

For a square footing according to Tezarghi’s theory;

q_ult = γD_fN_q + 0.4γbN_γ

N_q = 22.46
N_γ =19.13

(a) If the water table is at 5m below the surface, d (4 m) > B (2 m), hence the water table will have no effect on the bearing capacity;
q_ult = γD_fN_q + 0.4γbN_γ = (19 × 1 × 22.46) + (0.4 × 19 x 2 x 19.13) = 717.516 kN/m²

(b) If the water table is at the ground surface;
γD_f = D_f(γ_sat – γ_w) = 1m (19 – 9.81) = 9.19 kN/m²
γ′ = γ_sat – γ_w = (19 – 9.81) = 9.19 kN/m³
q_ult = γD_fN_q + 0.4γ’bN_γ = (9.19 × 22.46) + (0.4 × 9.19 x 2 x 19.13) = 347.05 kN/m²

(c) If the water table is at the bottom of the footing;
γD_f = (1m × 19) = 19 kN/m²
γ′ = γ_sat – γ_w = (19 – 9.81) = 9.19 kN/m³
q_ult = γD_fN_q + 0.4γ’bN_γ = (19 × 22.46) + (0.4 × 9.19 x 2 x 19.13) = 567.38 kN/m²

(d) If the water table is at 1m below footing;
γD_f = (1m × 19) = 19 kN/m²
ỹ = γ’ + d/B(γ – γ’) = 9.19 + [(1/2) × (19 – 9.19)] = 14.095 kN/m³
q_ult = γD_fN_q + 0.4ỹbN_γ = (19 × 22.46) + (0.4 × 14.095 x 2 x 19.13) = 642.45 kN/m²

From the results above, the following was observed;

(1) When the water table is at the ground surface, the bearing capacity reduces by 51.63%.
(2) When the water table is at the bottom of the footing, the bearing capacity reduces by 20.92%.
(3) When the water table is at 1m below the footing, the bearing capacity reduces by 10.46%.