How to Design Built-up Beams | Welded-Plate Girders

Sometimes, I-beam sections or girders are built up by welding structural steel plates together. This is usually done when the section required is so heavy that it cannot be picked from the standard sections available, or when the section required is not available with local manufacturers or dealers.

The difference between hot-rolled I-section and welded steel sections is shown in Figure 1. The design of a built-up beam (plate girder) involves the selection of adequate individual section sizes, weld sizes, and stiffeners (if required), and verifying their performance as a composite whole in satisfying ultimate and serviceability limit state requirements.

Design Example of Built-Up Beams

Ghosh (2010) presented an example of the design of a welded-plate girder for a crane gantry in an iron melting workshop/industry. The example has been reproduced here to show how to design welded-plate girders according to the requirements of EN 1993-1-1:2005.

Design Forces

Ultimate design vertical moment = M_vu = 29515 kNm
Ultimate design vertical shear force = V_vu = 6282 kN
Ultimate design horizontal moment = M_hu = 601 kNm
Maximum ultimate horizontal longitudinal tractive force = 312 kN
Span of girder = 24 m

Design of section
The section will be designed as a welded-plate girder. Eurocode 3, Part 1-1 (Eurocode, 2005) will be followed. The tables and figures referred to below can be found in Annex A of the Eurocode (Appendix B of this book), except where otherwise mentioned.

Design strength
By referring to Table 3.1 of Eurocode 3 (“Nominal values of yield strength f_y and ultimate tensile strength f_u for hot-rolled structural steel”), the design strength (f_y) in the ULS method of design for the flanges and web can be obtained; its value varies with the thickness of plate considered.

In our case, we adopt steel grade S275 with a design yield strength f_y = 275 N/mm². So, for a nominal plate thickness t ≤ 40 mm, f_y = 275 N/mm², and for t ≤ 80 mm, f_y = 255 N/mm². If the design strength of the web f_yw is greater than the design strength of the flange f_yf, then the design strength of the flange should always be used when considering moments or shear.

Initial sizing of section
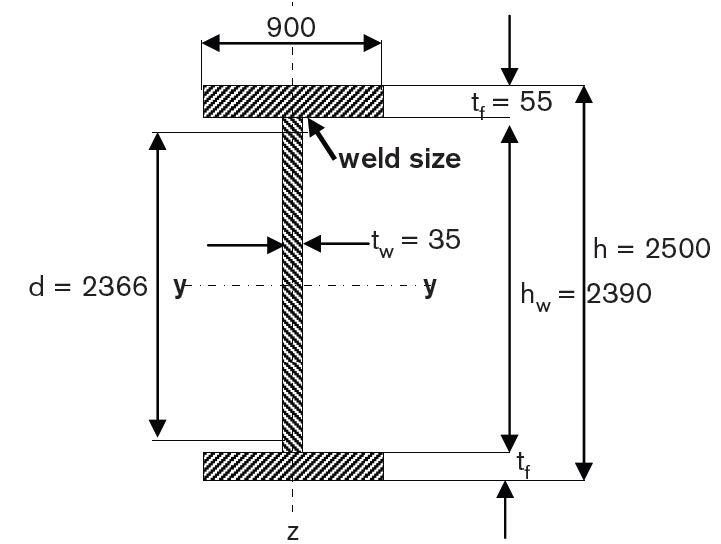
The dimensions of the webs and flanges are assumed to be as given below. Overall depth of girder = h. The depth should be chosen to limit the allowable deflection. In practice, the overall depth should normally be taken to be between 1/10 and 1/12 of the span. In our case, we assume the overall depth h = 1/10 of span = 23.4/10 = 2.34 m = 2340 mm. We assume an overall depth h = 2500 mm (as the girder is subjected to high dynamic wheel loads).

Depth of straight portion of web (d)
d = h − (2 × size of weld) − (2 × thickness of flange )= 2500 − 2 × 12 (assumed weld size) − 2 × 55 (assumed) = 2366 mm.

Breadth of flange (b)
The breadth of the flange should be at least 1/40 to 1/30 of the span in order to prevent excessive lateral deflection. In our case, we assume a breadth b = 1/30 of span = (1/30) × 23.4 = 0.78 m, say 0.9 m = 900 mm.

Thickness of web (t_w)
Several tests have shown that the web does not buckle owing to diagonal compression when the ratio d/t_w is less than 70, if the web is not stiffened by a vertical transverse stiffener. Referring to Table 5.2 (sheet 1) of Eurocode 3, Part 1-1, the minimum thickness of web required to avoid buckling of the compression flange in the ULS design method with an unstiffened web is as follows.

For class 1 classification,
d/t_w ≤ 72ε, where
ε = stress factor = (235/f_y)^0.5 = (235/255)^0.5 = 0.96;
d/t_w = 2366/t_w = 72 × 0.96
Therefore t_w = 2366/(72 × 0.96) = 34 mm

With a stiffened web and a spacing of transverse stiffeners a ≤ d,
t_w ≥ (d/250)(a/d)^0.5.
Assuming a spacing of stiffeners a = 2366 mm;
t_w = 2366/250 × (2366/2366)^0.5 = 10 mm.
We assume t_w = 30 mm.

Thickness of flange (t_f)
The minimum thickness of the flange required to limit the outstand of the flange is calculated as follows. The approximate flange area required is given by;

Af = Mvu/(hfy) = (29515 × 106)/(2500 × 255) = 46298 mm2
Assuming the width of the flange b = 900 mm
tf = 46298/900 = 51.4 mm.

We, therefore, assume t_f = 55 mm

Classification of cross-sections
Referring to Clause 5.5.2 of Eurocode 3, Part 1-1, the function of cross-section classification is to identify the extent to which the resistance and rotation capacity of the cross-section are limited by its local buckling resistance. In our case, we assume a class 1 cross-section classification without reduction of resistance. Thus, to determine the thickness t_f of the flange, we do the following.

For class 1 section classification, c/t_f ≤ 9ε,

where;
c = outstand of flange plate = [b − (t_w + 2 × 12 (weld size))]/2 = [900 − (25 + 24)]/2 = 425.5 mm.
Assuming t_f = 55 m,
c/t_f = 425.5/55 = 7.7 and 9ε = 9 × 0.96 = 8.64

Since c/t_f (7.7) < 9ε (8.64), the section satisfi es the conditions for class 1 section classification.
So we assume t_f = 55 mm.

To determine the thickness of the web t_w, we do the following;
For class 1 section classification, d/t_w ≤ 72ε. Assuming t_w = 30 mm,
d/t_w = 2366/30 = 78.9 and 72ε = 72 × 0.96 = 69 < d/t_w which does not satisfy the condition. We increase the thickness t_w to 35 mm.

d/t_w = 2366/35 = 67.6 < 72ε (69) which satisfies the condition. So, we assume t_w = 35 mm.

Thus the initial sizing of the section is as follows:

• Depth of girder h = 2500 mm.
• Breadth of flange b = 900 mm.
• Depth of straight portion of web d = 2500 − 2 × 55 − 2 × 12 (weld size) = 2366 mm.
• Thickness of web t_w = 35 mm.
• Thickness of flange t_f = 55 mm.
• Design strength with flange thickness 55 mm = f_y = 255 N/mm²
• Design strength of web with thickness 35 mm = f_y = 255 N/mm²

Although the design strength of the web is 275 N/mm² for 35 mm thickness, the lower value of f_y (255 N/mm²) of the flange should be considered in calculations for moments and shears.

Moment capacity
Total maximum ultimate vertical design moment = M_vu = 29515 kNm
Total maximum design shear = V_u = 6281 kN

The moment capacity should be calculated in the following way.
When the web depth-to-thickness ratio d/t_w ≤ 72ε, it should be assumed that the web is not susceptible to buckling, and the moment capacity should be calculated from the equation;

M_rd = f_yW_pl

provided the shear force V_Ed (V_vu) ≤ 0.5V_pl,rd (shear capacity),

where
M_rd = moment capacity,
W_pl = plastic section modulus
V_pl,rd = shear capacity.

In our case, d/t_w (67.6) < 72ε (69.1).
Thus, the web is not susceptible to buckling.

The ultimate shear force (V_vu) should also be less than half the shear capacity (V_pl,rd) of the section. Referring to equation (6.18) of Eurocode 3, Part 1-1;

V_pl,rd = A_v[f_y/(3)^0.5]/γM_o

where
A_v = shear area = dt_w + (t_w + 2r)t_f = 2366 × 25 + (25 + 2 × 12) × 50 = 61600 mm²

Referring to Clause 6.1, γM_o = partial factor = 1.0, and f_y = 335 N/mm² (because t_f > 40 mm).
Therefore plastic shear capacity V_pl,rd = 61600 × [335/(3)^0.5]/1.0/10³ = 12669 kN
and 0.5V_pl,rd = 12669/2 = 6335 kN > V_vu (6281 kN).

Thus, V_vu (6281 kN) < 0.5V_pl,Rd (6335 kN). So the section satisfies the conditions.

Since the web is not susceptible to buckling, and the lowest shear value in the section is less than half the shear capacity of the section, the moment capacity for this class 1 compact section should be determined by the “flange only” method. In this case, the whole moment will be taken up by the flanges alone and the web takes the shear only.

Therefore moment capacity of section M_y,Rd = f_yA_fh_s

where;
A_f = area of compression flange = b × t_f = 900 × 55 = 49500 mm²
h_s = depth between centroids of flanges = 2500 − 55 = 2445 mm
f_y = 255 N/mm²

Therefore;

M_y,Rd = 255 × 49500 × 2445/10⁶ = 30862 kNm > M_Ed (M_vu) (29515 kNm). Satisfactory

Alternatively, referring to Clause 6.2.5, the moment capacity of the section may be expressed by the following equation:

M_pl,Rd = W_plf_y/γM_o

The plastic modulus is calculated to be 1.71008 x 10⁸ mm³
M_pl,Rd = W_plf_y/γM_o = [(1.71008 x 10⁸ × 255)/1.00] × 10^-6 = 43607 kNm

where W_pl is the plastic modulus of the section. As the section assumed is built-up welded and of high depth, no rolled I section is available of this depth. The plastic modulus for the assumed depth can be calculated. So the above equation can only be used when the assumed section is manufactured industrially by welding.

In addition, the top flange is also subjected to a stress due to the horizontal transverse moment caused by horizontal crane surges. Therefore, the “flange only” method is suitable in our case. The horizontal transverse ultimate moment M_hu is equal to 601 kN m.

This transverse horizontal moment is resisted by a horizontal girder formed by the connection of the 6 mm plate (acting as a web) of the walking platform (Durbar), between the top flange of the main plate girder and the tie beam at the walking-platform level. Distance between centre line of plate girder and the tie beam = h_z = 2.5 m

Horizontal moment of resistance = M_z,Rd = f_yA_fh_z
where A_f = area of top flange = 900 × 55 = 49500 mm².

Therefore
M_z,Rd = 255 × 49 500 × 2500/10⁶ = 31556 kNm > M_hu (601 kNm)

Referring to the criterion based on the quantity;

[M_y,Ed/M_y,Rd]^α + [M_z,Ed/M_z,Rd]^β

where α and β are constants, which may conservatively be taken as unity.

This quantity is equal to
[29515/30862] + [601/31556] = 0.95 + 0.02 = 0.97 < 1 Satisfactory

Therefore we adopt the section for the welded-plate girder. For other design checks such as buckling and stiffness design, see Ghosh (2010).

Source:
Ghosh K. M (2010): Practical Design of Steel Structures. Whittles Publishing, UK