In some cases, the foundation of buildings may be founded on or very close to natural or man-made earth slopes. The bearing capacity of shallow foundations on slopes is reduced because the full formation of shear zones under ultimate loading conditions is not possible on the sides close to the slopes or edges. This is due to the fact that the zones of plastic flow in the soil on the slope side are smaller than those in a similar foundation on level ground, thereby resulting in a lower ultimate bearing capacity.
Meyerhof (1957) extended his bearing capacity theory to account for the effect of slope on the bearing capacity of foundations. Many other recent research works have been conducted on the effect of slope on bearing capacity using finite element modelling (Acharyya and Dey, 2017; Chakraboty and Kumar, 2013) and energy dissipation methods (Yang et al, 2007).
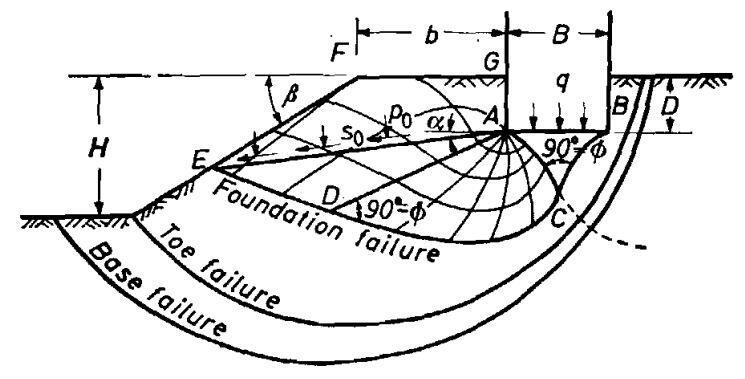
Figure 1 shows a section of a foundation with the failure surfaces under ultimate loading conditions. The distance b between the top edge of the slope and the foundation face determines the foundation’s stability. For a strip footing, the ultimate bearing capacity equation can be written as:
q = CNcq + 0.5γBNγq —– (1) (Meyerhof, 1957)
where γ = unit weight of soil, B = width of foundation, and Ncq and Nγq = resultant bearing capacity factors depending on the angle of inclination of the slope (β), angle of shearing resistance of the soil (ϕ), and the depth/width ratio D/B of the foundation.
The bearing capacity factors decrease with a greater inclination of the slope to a minimum for β = 90 degrees on purely cohesive material, and β = ϕ on cohesionless soil, when the slope becomes unstable. Because the bearing capacity of cohesionless soils is found to decrease approximately parabolically with an increase in slope angle, the decrease in bearing capacity is small in the case of clays but can be significant in the case of sands and gravels for inclinations of slopes used in practice (β < 30 degrees).
A solution of the slope stability has been obtained for a surcharge across the full horizontal top surface of a slope using dimensionless parameters called the stability number Ns, written as given in Equation (2);
Ns = c/γH —– (2)
Where c is the cohesion of the soil, γ is the unit weight of the soil, and H is the vertical height of the slope.
Eq. (3) represents the bearing capacity of a foundation on purely cohesive soil of great depth;
q = CNcq + γDf —— (3)
where the Ncq factor depends on b as well as β, and the stability number Ns. This bearing capacity factor decreases significantly with increasing height and to a lesser amount with increasing slope inclination, as shown in the lower regions of Figure 2. The bearing capacity factor increases with an increase in b for a given height and slope angle, and beyond a distance of about 2 to 4 times the height of the slope, the bearing capacity is independent of the slope angle.
These bearing capacity factors are given in Figures 2 and 3 for strip foundation in purely cohesive and cohesionless soils respectively.
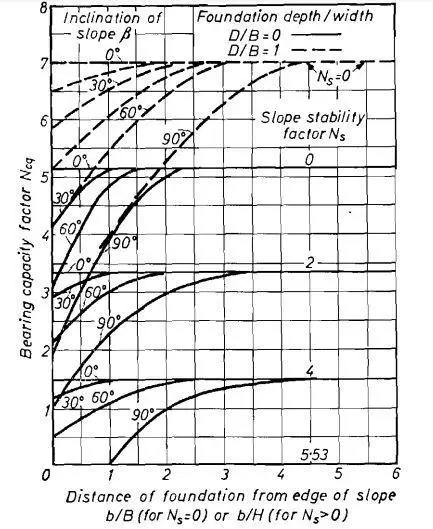
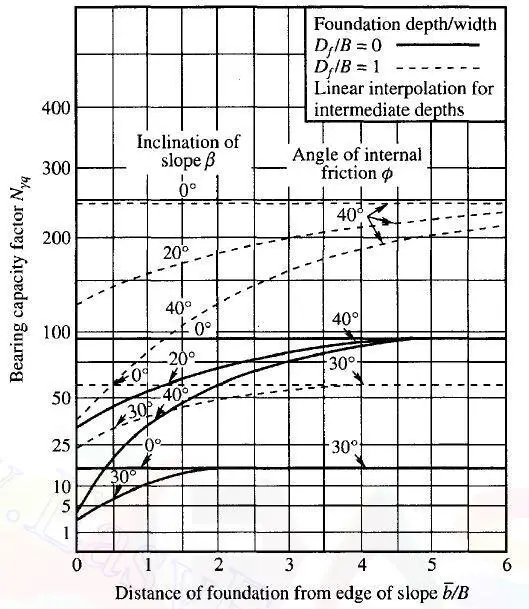
The bearing capacity factors increase with an increase in distance b. Beyond a distance of about 2 to 6 times the foundation width B, the bearing capacity is independent of the slope’s inclination and becomes the same as that of a foundation on a level surface.
References
[1] Acharyya R. and Dey A. (2017): Finite Element Investigation of the Bearing Capacity of Square Footings Resting on Sloping Ground. INAE Lett (2017) 2:97–105 DOI 10.1007/s41403-017-0028-6
[2] Debarghya Chakraborty & Jyant Kumar (2013) Bearing capacity of foundations on slopes, Geomechanics and Geoengineering, 8:4, 274-285, DOI: 10.1080/17486025.2013.770172
[3] Meyerhof G. G. (1957): The ultimate bearing capacity of foundations on slopes. The Proceedings of the Fourth International Conference on Soil Mechanics and Foundation Engineering, London, August 1957
[4] Yang, Xl., Wang, Zb., Zou, Jf. et al. (2007): Bearing capacity of foundation on slope determined by energy dissipation method and model experiments. J Cent. South Univ. Technol. 14, 125–128 (2007). https://doi.org/10.1007/s11771-007-0025-0










