Theorem of Parallel Axis

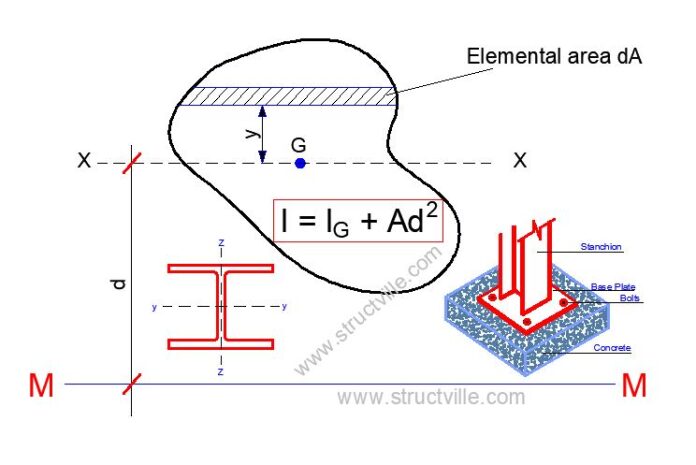
The theorem of parallel axis (also known as Huygens-Steiner theorem) states that the moment of inertia (I) of an area (A) with respect to a given axis is equal to the sum of the moment of inertia (I_G) of that area with respect to the parallel centroidal axis and the product Ad², where d is the distance between the two axis.

I = I_G + Ad²

When examined by itself, there is no physical significance for moment of inertia. It is just a mathematical expression denoted by I. When mass moment of inertia is used in conjunction with the rotation of rigid bodies, it can be regarded as the measure of the resistance of the body to rotation. However, in the deflection of structures, the moment of inertia (second moment of area) of a body is an indication of the flexural rigidity of the body or the resistance to bending or deformation.

The theorem of parallel axes is not limited to a single body. It can be generalized to systems of rigid bodies by summing the individual moments of inertia about respective parallel axes. Additionally, variations like the perpendicular axis theorem apply specifically to planar bodies, relating the moment of inertia about an axis perpendicular to the plane to those about two in-plane axes.

The theorem of parallel axis is used in the calculation of the moment of inertia of composite shapes used in civil engineering such as I-sections (universal beams), T-sections, channel sections, angle sections, etc. The moment of inertia is used in the calculation of deflection and an indication of the stiffness of structural members.

Proof of the Theorem of Parallel Axis

In the figure shown below, we have a lamina with an area A. Let M-M be the axis in the plane of the lamina about which the moment of inertia is sought. Let X-X be the centroidal axis in the plane of the lamina parallel to the axis M-M. Let d be the distance between the two axes X-X and M-M.

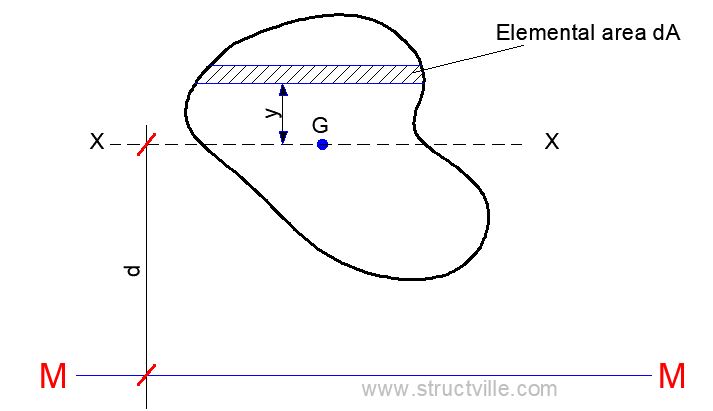
It may be assumed that the lamina consists of an infinite number of small elemental components parallel to the axis X-X. Let us consider one of such elemental components parallel to the at a distance y from the axis X-X. The distance of the elemental component from the axis M-M will be (d + y) accordingly.

Moment of inertia of the elemental component about the axis MM = I_MM = ∑dA (d + y)²
I_MM = ∑dA (d + y)² = ∑dAd² + ∑dAy² + 2∑dAhy
= d²∑dA + ∑dA∙y² + 2h∑dA∙y

But,
∑dA = A
d²∑dA = Ad²
∑dA∙y² = moment of inertia about the X-X axis = I_G
∑dA∙y = 0, since X-X is the centroidal axis.

Therefore; I_MM = I_G + Ad² which is the theorem of parallel axis.

Solved Example

Calculate the moment of inertia of the T-section shown below.

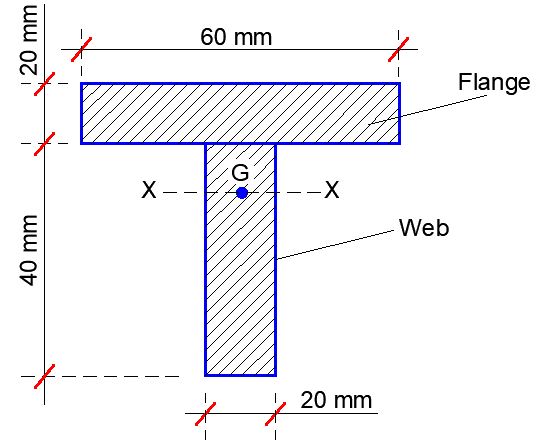
To obtain the moment of inertia of the section, we can break the T-section into its two basic components (flange and web). The first step is to determine the location of the centroid of the shape with respect to X-X. We can easily create a table for such calculations.

Component	Area (A) (mm2)	Centroidal distance (y) from the base (mm)	Ay (mm3)
Flange	60 × 20 = 1200	40 + (20/2) = 50	60000
Web	40 × 20 = 800	40/2 = 20	16000

∑A = 1200 + 800 = 2000 mm²
∑Ay = 60000 + 16000 = 760000 mm³

Centroid ŷ = ∑Ay/∑A = 760000/2000 = 38 mm

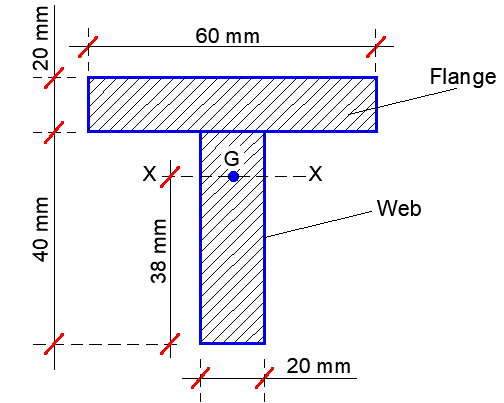
I_xx = I_xx,flange + I_xx,web

Using the parallel axis theorem, I = I_G + Ad²

I_xx,flange = (60 × 20³)/12 + [(60 × 20) × (50 – 38)²] = 212800 mm⁴
I_xx,web = (20 × 40³)/12 + [(40 × 20) × (38 – 20)²] = 365866.667 mm⁴
I_xx = I_xx,flange + I_xx,web = 212800 + 365866.667 = 578666.667 mm⁴

Note: The moment of inertia of a simple rectangle about its centroidal axis (I_G) is given by bd³/12