Uplift Capacity of Piles

In the design of pile foundations, it is usually very common to express the load carrying capacity in terms of axial compression. However in some cases, piles are subjected to uplift forces, and must be designed to resist such forces in order to avoid the pull out of the foundation or the structure. Piles that are subjected to uplift forces are also called tension or anchor piles. Uplift forces are developed due to hydrostatic pressure or overturning moments.

Forces due to earthquake, wind, or waves, are the major actions that can induce uplift forces in piles. Structures such as transmission towers, mooring systems for ocean surface or submerged platforms, tall chimneys, jetty constructions, etc., all have their foundations subject to uplift loads.

Factors Affecting Uplift Capacity

Several factors influence the uplift capacity of piles and they are briefly described below.

1. Soil Characteristics: Soil properties, including the cohesion and friction angle, significantly affect uplift capacity. Clay soils will rely on the cohesion or unit adhesion of the soil with the pile material for uplift resistance, while granular soils will rely on frictional forces (dependent on the angle of internal friction) for uplift resistance.
2. Pile Geometry: The shape, size, and length of the pile influence its uplift capacity. Longer piles provide a larger surface area in contact with the soil, thus increasing resistance against uplift forces. Additionally, the pile diameter and shape can affect the distribution of uplift forces along the pile shaft. It is also important to note that pile cap dimensions and group effects can also influence the uplift capacity of piles.
3. Pile Material: The material used for pile construction plays a role in uplift capacity. Steel piles are often preferred due to their high strength and ductility, providing better resistance against uplift. However, other factors, such as corrosion potential, must also be considered. Furthermore, scholars have also determined that the angle of wall friction between the pile and the surrounding soil is dependent on the pile material.
4. Pile Installation Method: The uplift capacity is typically higher in driven piles than bored piles.
5. Groundwater Conditions: The level of groundwater significantly affects uplift capacity. In saturated soil conditions, the presence of water can reduce the soil’s effective stress, potentially reducing the uplift resistance of piles. Conversely, dewatering or densification techniques can improve uplift capacity.

Methods for Determining Uplift Capacity

Uplift capacity of piles may be assessed using theoretical analyses (classical equations developed using soil properties), field tests, and numerical modeling. The following are commonly used approaches:

1. Analytical Methods: Several analytical methods, such as the Terzaghi’s equation and the Vesic’s method, provide simplified solutions to estimate uplift capacity. These methods typically consider soil parameters, pile geometry, and groundwater conditions to calculate the uplift resistance.
2. Field Load Tests: Load tests conducted in the field help validate the design assumptions and provide valuable data on the actual uplift capacity. Common load test methods include the pile load test, plate load test, and pile uplift test. These tests involve applying controlled loads to the pile and measuring its response to determine uplift capacity.
3. Numerical Modeling: Finite element analysis (FEA) and other numerical modeling techniques allow engineers to simulate complex soil-pile interactions and evaluate uplift capacity. Numerical models consider soil behavior, pile-soil interaction, and other relevant factors to provide detailed insights into the uplift response.

Generally, the equation for uplift capacity of a single pile may be written as;

P_ul = W_p + A_sf_r ——– (1)

where,
P_ul = uplift capacity of pile,
W_p = weight of pile,
f_r = unit resisting force
A_s = effective surface area of the embedded length of pile.

Uplift capacity of pile in clay

For piles embedded in clay, equation (1) may be written as;

P_ul = W_p + A_sαc_u ——– (2)

where,
c_u = average undrained shear strength of clay along the pile shaft,
α = adhesion factor (= c_a/c_u),
c_a = average adhesion

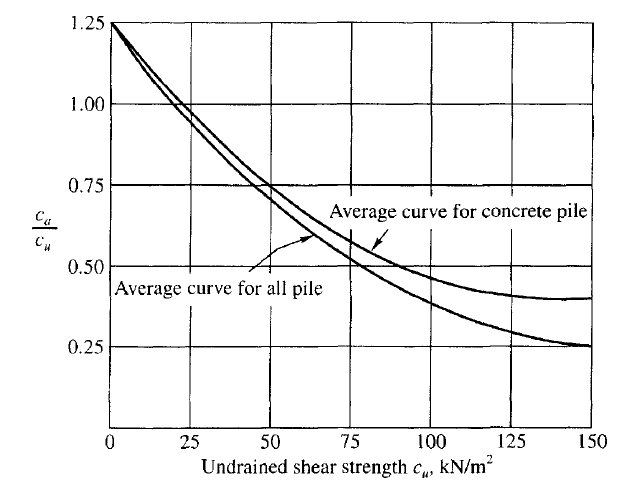
Figure 1 gives the relationship between α and c_u based on pull out test results as collected by Sowa (1970). As per Sowa (1970), the values of c_a agree reasonably well with the values for piles subjected to compression loadings.

Uplift capacity of pile in sand

The ultimate uplift capacity of a vertical pile for piles embedded in sandy soil depends on the skin resistance created between the pile shaft and the soil.

According to Murthy (2012), adequate confirmatory data are not available for evaluating the uplift resistance of piles embedded in cohesionless soils. Ireland (1957) reports that the average skin friction for piles under compression loading and uplift loading are equal, but data collected by Sowa (1970) indicate lower values for upward loading as compared to downward loading especially for cast-in-situ piles. A study by Ramasamy et al. (2004) showed that the pull out shaft friction is significantly less than the push in shaft friction.

Poulos and Davis (1980) suggest that the skin friction of upward loading may be taken as two-thirds of the calculated shaft resistance for downward loading.

According to Verma and Joshi (2010), the net uplift capacity of piles embedded in sand can be given by the equation (3) as:

Q_u = ½ K_s σ_v tanδ πdZ_c + K_s σ_v tanσ π(L – Z_c) ——– (3)

Where;
K_s = coefficient of earth pressure
σ_v = effective vertical stress at a depth of Zc = γ_dZ_c
d = diameter of pile
γ_d =dry unit weight of soil
δ = soil-pile friction angle
L = Length of pile
Z_c or L_cr = critical depth of embedment

According to Verma and Doshi (2010), the value of coefficient of earth pressure in Equation (3) has a large range of 0.3 to 4.0, which implies that there are many implications to the value of K_s.

Solved Example

A 450 mm diameter pile is embedded in a homogenous medium dense sand, determine the net pullout capacity (FOS = 3.0). Given: L = 12 m, φ = 38°, K_s = 1.5, and δ = 25°, γ_(average) = 17 kN/m³
The water table is at great depth, and take the critical depth to be 15D.

Solution

Critical depth = 15 × 0.45 = 6.75 m
σ_v = 6.75 × 17 = 114.75 kN/m²

f_s = 114.75 × 1.5 × tan 25 = 80.263 kN/m²

f_s1 = ½ f_sπdZ_c = ½ × 80.263 × π × 0.45 × 6.75 = 382.9 kN
f_s2 = f_sπd(L – Z_c) = 80.263 × π × 0.45 × (12 – 6.75) = 595.71 kN

Total skin resistance = f_s1 + f_s2 = 382.9 + 595.71 = 978.61 kN

Q_a = 978.61/3 = 326.2 kN (Factor of safety of 3)

After Poulos and Davis (1980), pull out capacity = 2/3 × 326.2 = 217.46 kN

Conclusion

The uplift capacity of piles is an important factor in the design of structures that are subjected to uplift loads. Geotechnical design of piles must ensure that the uplift capacity of the piles is sufficient to resist the expected loads. There are a number of equations that can be used to estimate the uplift capacity of piles, but the final design should be based on the specific soil conditions and the design requirements.

References

Ireland, H.O. (1957). “Pulling Tests on Piles in Sand,” Proc. 4th Int. Conf. SM and FE, Vol. 2.
Murthy V.N.S (2012): Geotechnical Engineering. Marcel Decker Inc. New York
Poulos, H.G., and Davis, E.H. (1980). Pile Foundation Analysis and Design, John Wiley & Sons, New York.
Ramasamy, G., Dey, B. and Indrawan, E. (2004): “Studies on skin friction in piles under tensile and compressive load”, Indian Geotechnical Journal, Vol. 34, No. 3, pp. 276-289.
Sowa, V.A. (1970). “Pulling Capacity of Concrete cast-in-situ Bored Pile,” Can. Geotech. J., Vol. 7.
Verma A. K. and Joshi R. K. (2010): Uplift Load Carrying Capacity of Piles in Sand. Indian Geotechnical Conference – 2010, GEOtrendz pp 857 – 860