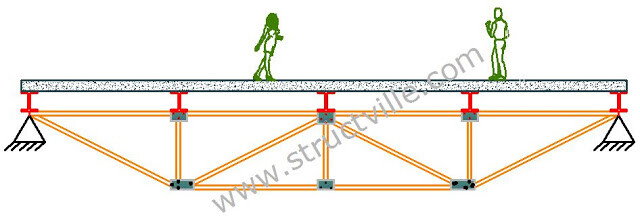
Introduction
Indeterminate trusses are analysed usually analysed using force method or direct stiffness method. In this post, we are going to analyse step by step, the analysis of the truss loaded as shown below.
(EA = Constant)
Step 1: Determine the degree of static indeterminacy
For a truss to be determinate;
m + r = 2j
Where;
m = number of members = 13
r = number of support reactions = 4
j = number of joints = 8
Therefore;
13 + 4 – 2(8) = 1
Therefore, the truss is indeterminate to the 1st order at the supports.
Step 2: Select redundant and remove constraint
To solve for the single degree of indeterminacy, the structure has to be reduced to a statically determinate and stable structure. This can be achieved by removing a redundant support, and a little consideration will show that for the structure to be stable, only a horizontal redundant will have to be removed. In this case, let us remove the horizontal support at H. This will give us the basic system that is given below.
Step 3: Analyse the basic system completely and obtain the internal forces
We now have to obtain the support reactions and internal forces using the principles of statics.
Support Reactions
Geometrical Properties
θ = tan-1(2/4) = 26.57°
∑Fy = 0
-FAC sinθ + 9.63 = 0
FAC = 9.63/sin 26.57° = 21.53 kN (Tension)
∑Fx = 0
FAB + FAC cosθ – 3 = 0
FAB = 3 – (21.53 cos 26.57) = -16.27 kN (Compression)
Joint B
∑Fy = 0
-FBC – 4 = 0
FBC = -4kN (Compression)
∑Fx = 0
-FAB + FBD = 0
FAB = FBD = -16.27 kN (Compression)
To simplify our analysis, we can obtain the forces in members CE and CD through the method of sections.
∑Fy = 0
-FGH sinθ + 9.37 = 0
FGH = 9.37/sin 26.57° = 20.95 kN (Tension)
∑Fx = 0
-FFH – FGH cosθ = 0
FFH = -(20.95 cos 26.57) = -18.74 kN (Compression)
Joint E
∑Fy = 0
FED + 0 = 0
FED = 0 (No force)
∑Fx = 0
-FCE + FEG = 0
FCE = FGE = 30.52 kN (Tension)
Joint D
∑Fy = 0
-FDC sinθ – FDG sinθ – 10 = 0
-(-12.59 sinθ) – FDG sinθ – 10 = 0
FDG = -4.37/sin 26.57° = -9.77 kN (Compression)
Step 4: Calculate the deformation at the redundant
Having obtained the internal forces at the redundant, we can now use virtual work method to calculate the horizontal translation at support H which corresponds to the removed redundant Hx. This is done by removing the external load on the basic system and applying a unit horizontal force in the direction of the removed force.
By looking at what is happening at the above structure, you will agree with me that the entire top chord is in a uniform compression of -1.0 kN.
Hence;
FAB = FBD = FDF = FFH = -1.0 (Compression)
All other members of the truss have zero forces.
Since the horizontal displacement at H in the original structure is equal to zero, it means that the horizontal reaction at support H must produce a deflection in the opposite direction that will counter the deflection.
Deformation of the basic system due to externally applied load can be obtained by using the relationship below;
Where;
m = number of members
n = Internal forces due to virtual load
N = Internal forces due to externally applied load
L = Length of member
A = Cross sectional area of member
E = Modulus of Elasticity of member
To analyse it, we normally present this in tabular form. Due to the fact that the force in the members in the virtual load state are zero in all members except the top chord, we will just focus on the top chord.
δ1P = 2(65.08/AE) + 2(74.96/AE) = 280.08/AE
The deflection at point H due to the virtual load can be obtained using the same relationship, and this is shown in the table below;
δ11 = 4(4/AE)) = 16/AE
The appropriate cannonical equation is therefore given by;
δ11X1 + δ1P = 0
On substituting;
16X1 + 280.08 = 0
X1 = -17.51 kN ←
Therefore, the horizontal reaction at H (Hx) is 17.51 kN←
Having obtained this, we can now analyse the truss again to obtain the final internal forces.
We are always happy to have you around at Structville.
Have you read…
Analysis of Statically Indeterminate Frames Using Force and Displacement Methods
Our interactive facebook page is at;
www.facebook.com/structville