Design of Piles in Sand: Case Study of Lekki Pennisula, Lagos Nigeria

Construction experts in Lagos Island, Nigeria are no strangers to pile foundation. The poor soil profile in the area means that foundations are more economically founded at depths way beyond the weak upper soil strata. Faseki et al (2016) carried out assessment of sub-soil properties of some parts of Lekki Peninsula, Lagos.

The result of their findings form the basis of this post, which aims to explore the  design of pile foundations on sand, using Eurocode 7, and Lekki, Lagos State Nigeria, as case study. The summary of their findings regarding geotechnical properties of the soil in the area is given in the Table below;

The reports from soil investigation in most parts of Lekki indicate poor bearing capacity for shallow foundations. In a research work by Warmate and Nwankwoala (2019), an average bearing capacity of 55 kN/m² was reported within 1m depth of the soil using direct shear analysis and SPT. However, in an independent soil investigation report carried out within Abijo Village, Ibeju Lekki, fibrous peat was observed within 0 – 5m depth of the area, necessitating the adoption of pile foundation in such areas.

Theoretical Background of Pile Foundation Design

When the static formulae is applied in the geotechnical design of piles, the ultimate load carrying capacity is calculated from the soil properties obtained from site investigation. This tends to be a more natural approach since it is the soil that actually carries the load, but more often than not, pile load tests are employed for validation of results. The ultimate capacity of piles is assumed to be reached when;

Q_u = Q_b + Q_s + W_s ——- (1)

Where:
Q_u = Ultimate capacity of pile
Q_b = Base resistance = q_uA_b
Q_s = Shaft resistance = f_uA_s
W_s = Weight of displaced soil

Quite often, the weight of the pile and the weight of the soil removed is assumed to be equal, such that the last term of the equation is eliminated.

q_u = ultimate value of the resistance per unit area of the base due to shear strength of the soil
f_u = ultimate value of the tangential force per unit area of the shaft due to adhesion and skin friction
A_s = surface area of the pile shaft
A_b = base area of the pile
L = Length of pile below ground.

Meyerhof (1951) expressed the base resistance per unit area as;

q_u = cN_c + k_sP_o‘N_q + 0.5BγN_γ   ———(2)

In the case of a pile of normal proportions, L/B is about 30 or more, the term containing B in the above equation is so small that is usually ignored. The above equation now reduces to;

q_u = cN_c + k_sP_o‘N_q  ———-(3)

Where;
k_s = the coefficient of earth pressure on the shaft within the failure zone
N_c, N_q = Bearing capacity factors dependent on the embedment ratio and angle of internal friction

In a soil where both adhesion and friction can be mobilised on the pile shaft, Meyerhof (1951) expressed the tangential force per unit area as;

f_u = C_a + k_sP_o‘tanδ ——— (4)

Where;
C_a = adhesion per unit area
δ = angle of friction between the soil and the pile material
For a purely cohesive soil such as clay, δ is zero and for non-cohesive soil such as sand, C_a is zero.

Pile Foundation in Sand

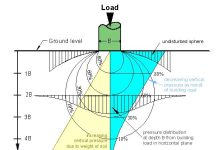
Knowing full well that in purely cohesionless soil (sand), f_u = k_s‘P_o‘tanδ. What this equation means is that the skin friction continues to increase linearly with increasing depth. But for piles founded on sand, it has been determined that the overburden pressure of the soil adjacent to the pile does not increase without limits. When a certain depth of penetration is reached, the overburden pressure remains more or less constant, and this is called the critical depth D_c.

The critical depth depends on the field condition and the dimensions of the pile. It is generally agreed that at a penetration depth between 10 and 20 pile diameters, a peak value of skin friction is reached which cannot be exceeded at greater penetration depth (see figure below). Therefore, the equation f_u = k_s‘P_o‘tanδ gives increasingly unsafe values as the penetration depth increases and exceeds about 20 pile diameters. The assumptions usually made for piles as reported by Wrana (2015) are;

• Pile in loose sand (10D)
• Pile in medium dense sand (15D)
• Pile in dense sand (20D)

Figure 1: Critical Depth For Pile Founded on Sand (Picked from Wrana, 2015)

Therefore, for piles in a homogenous dense sand for example;
Q_u = Q_b + Q_s = q_u.A_b + f_u.A_s

Total skin friction = f_u.A_s = k_s‘tanδ × Area of PV diagram × Circumference of pile
Area of PV diagram = 0.5γ.D_c²
But D_c = 20B
q_u = Pv. N_q = γ.D_c

Therefore;
f_u.A_s = k_s‘tanδ × 0.5γ.D_c² × πD
q_u.A_b = (γ.D_c)(N_q)(πD²/4)

The working load or design load for all pile types is equal to the sum of the base resistance and the shaft friction divided by a suitable factor of safety.

Pile Design to Eurocode 7 (EN 1997-1:2004)

EN 1997-1 clause 7.4(1)P states that the design of piles shall be based on one of the following approaches:

(1) The results of static load tests, which have been demonstrated by means of calculations or otherwise, to be consistent with other relevant experience,
(2) Empirical or analytical calculation methods whose validity has been demonstrated by static load tests in comparable situations,
(3) The results of dynamic load tests whose validity has been demonstrated by static load tests in comparable situations,
(4) The observed performance of a comparable piles foundation, provided that this approach is supported by the results of site investigation and ground testing.

Pile Resistance from ground parameters 

According to clause 7.6.2.3(8) pf EC7, the characteristic base and shaft resistances may also be determined directly from the ground parameters using the following equations;

R_b;k = A_b q_b;k
R_s;k = ∑A_s;i q_s;i;k

Where;
q_b;k  is the characteristic unit base resistance
q_s;i;k  is the characteristic unit shaft resistance

The design compressive resistance of a pile R_c,d may be obtained either by treating the pile resistance as a total resistance;

R_c,d = R_c;k / γ_t  (where R_c;k = R_b;k +  R_s;k)

or by separating it into base and shaft components R_b;k and R_s;k using the relevant partial factors, γ_b and γ_s

R_c,d = [R_b;k / γ_b  + R_s;k / γ_s]

The partial resistance factors in the UK National Annex have been modified to take account of the type of pile and whether the serviceability behaviour is to be determined either by load test or a rigorous and reliable calculation (Raison 2017).

The table below gives the partial factors for bored piles (culled from Raison, 2017)

The equilibrium equation to be satisfied in the ultimate limit state design of axially loaded piles in compression is F_c,d  ≤ R_c,d .

Example of Pile Foundation Design for Lekki Peninsula

A structure to be built at Lekki Peninsula, Lagos has a group of piles to be subjected to a characteristic permanent load (G_k) of 665 kN and characteristic variable load Q_k of 275 kN each. It has been decided to use piles of diameter 600mm, and soil investigation report from Faseki et al (2016) is to be used for the design. The design involves determining the length of embedment of the piles.

Solution

For details of this calculation and approach, go to clause 7.6.2.3 of EN 1997-1:2004.

Let us make an initial trial of 20m depth.

For this particular design, we will ignore the effect of shaft resistance on the first and second layers. Our interest is to determine the appropriate length of penetration into the fourth layer or possibly fifth layer. We are assuming that the water table lies at 1m below the ground.

For simplicity, let me summarise the properties of the layers below as reported by Faseki et al (2016);

First layer (3m thick) – Loose to Medium Silty Sand, C_u = 0, ϕ = 32°, γ = 18.5 kN/m²
Second layer (1.5m thick) – Soft silty clay, C_u = 24 kN/m² , ϕ = 28°, γ = 15 kN/m²
Third layer (4.5m thick) – Very loose sand,  Cu = 0, ϕ = 30°, γ = 18.5 kN/m²
Fourth layer (11m thick) – Medium dense sand,  Cu = 0, ϕ = 33°, γ = 19.5 kN/m²

The decision to ignore the shaft (friction) resistance of the first two layers is conservative. I am not very confident about the behaviour of the 1st layer, and the clay layer (2nd layer) sandwiched between the upper and lower sandy formations. But a little consideration shows that the 3rd and 4th layer gives more confidence for design purposes.

(1) Calculation of the Base Resistance
Base resistance R_b;k = q_b:k.A_b = (P_o‘)(N_q)(πD²/4)

From Faseki’s report, the angle of internal friction at layer of interest φ = 33°

N/B: Table A.4 of EC7 recommends that we apply material factor of safety to some soil properties, but UK Annex to EC7 does not recommend application of partial safety factors except in the case of negative skin friction.

Values of bearing capacity factor N_q according to NAVFAC DM 7.2(1984), is given below;

From the table above; N_q at the receiving layer = 17 (pile will be bored)
Effective pressure at the base of the pile = (18.5 × 3) + (15.5 × 1.5) + (18.5 × 4.5) + (19.5 × 11) = 376.5 kN/m²
Pore water pressure = 10kN/m³  × 19m = 190 kN/m²
Effective Stress at foundation depth = 376.5 – 190 = 186.5 kN/m²

Base resistance = q_b:k × A_b = (186.5 × 17) × (π × 0.6²/4) = 896.553 kN

(2) Shaft Friction
We will ignore the shaft resistance of the first two layers as earlier stated, but typical calculation values are shown.

f_u.A_s = k_s‘ tanδ × 0.5P_o‘ × πDL

Typical values for δ and k_s‘ as suggested by Broms (1966) is given in the table below.

For the first layer (loose sand);
δ = 0.75ϕ = 0.75 × 32 = 24°
(tan 24°) = 0.445
Effective stress at the layer = (18.5 × 3) – (10 × 2) = 35.5 kN/m²
f_u1.A_s1 = 1.0 × 0.445 × (0.5 × 35.5) × (π × 0.6 × 3) = 44.672 kN

For the second layer (silty clay);
Cohesion of soil C_u = 24.0 kN/m²
α = 1.0 since C_u < 25 kN/m² (Wrana, 2015)
q_s.A_s = 1.0 × 25 × (π × 0.6 × 1.5) = 70.695 kN

But we are neglecting the effects of these on the pile

For the third layer (loose sand);
δ = 0.75ϕ = 0.75 × 30 = 22.5°
(tan 22.5°) = 0.4142
Effective stress at the layer = (18.5 × 3) + (15.5 × 1.5) + (18.5 × 4.5) – (10 × 8) = 82.5 kN/m²
f_u3.A_s3 = 1.0 × 0.4142 × (0.5 × 82.5) × (π × 0.6 × 4.5) = 144.945 kN

For the fourth layer (medium dense sand);
δ = 0.75ϕ = 0.75 × 33 = 24.75°
(tan 24.75°) = 0.461
Effective stress at the layer = 186.5 kN/m²
f_u3.A_s3 = 1.5 × 0.461 × (0.5 × 186.5) × (π × 0.6 × 11) = 1337.184 kN

Therefore, total load from shaft resistance R_s;k = 144.945 + 1337.184 = 1482.129 kN

Design Approach 1

Combinations of sets of partial factors
DA1.C1  —–     A1 + M1 + R1
DA1.C2  ——-   A2 + M1 or M2 + R4

Partial factors for actions;
A1   γ_G = 1.35   γ_Q = 1.5
A2   γ_G = 1.0     γ_Q = 1.30

Partial factors for materials
M1 and M2 not relevant (γϕ’ = 1.0, not used)

Partial Resistance factors
R1    γ_b = 1.0    γ_t = 1.0
R4    γb = 1.3      γ_t = 1.3

DA1.C1   F_c,d = 1.35G_k + 1.5Q_k = (1.35 × 665) + (1.5 × 275) = 1310.25 kN
DA1.C2   F_c,d = 1.0G_k + 1.3Q_k = (1.0 × 665) + (1.3 × 275) = 1022.5 kN

By UK National Annex (with no SLS verified);

DA1.C1   
R_c,d = R_b;k/γ_b + R_s;k/γ_s = [896.55/2 + 1482.129/1.6] = 1374.6 kN

Also check;
R_c,d = R_c,k/γ_t = [896.55 + 1482.129] / 2.0 = 1189.3395 kN

R_c,d (1189.3395 kN) < F_c,d (1310.25 kN)

DA1.C2   
R_c,d = R_b;k/γ_b + R_s;k/γ_s = [896.55/(1.3 × 2) + 1463.681/(1.3 × 1.6)]  = 1048.518 kN
R_c,d (1048.518 kN) > F_c,d (1022.5 kN)

Therefore, Design Approach 1 Combination 1 (DA1.C1) is more critical, and pile length will need to extend beyond 20m length. Therefore from Design Approach 1, Combination 1, the length of 20m is rejected.

Design Approach 2

Combinations of sets of partial factors
DA2  —–     A1 + M1 + R2

Partial factors for actions;
A1   γ_G = 1.35   γ_Q = 1.5

Partial factors for materials
M1 not relevant (γϕ’ = 1.0, not used)

Partial Resistance factors
R2    γ_t = 1.1 (Total/combined compression)

F_c,d = 1.35G_k + 1.5Q_k = (1.35 × 665) + (1.5 × 275) = 1310.25 kN

DA2
R_c,d = R_b;k/γ_b + R_s;k/γ_s = [896.55/(1.1 × 2) + 1482.129/(1.1 × 1.6)]  = 1249.641 KN
R_c,d (1249.641 kN) > F_c,d (1310.25 kN)

Hence Length of 20m is rejected using Design Approach 2

Conclusion

We have seen from the design that the pile length of 20m at a diameter of 600mm is inadequate to support the design load specified. An alternative is to increase the diameter of the pile, but the reader should pay close attention to the assumptions made in arriving at the ultimate values.

The probable shaft resistance of the rejected two layers was shown, so that it could serve as a guide for judgement and further decision making. However, the closeness of the answers offer very intellectually stimulating ideas about the assumptions made However, I will also be happy if I can get an alternative design based on the soil properties, which might include the SPT and CPT values reported for the various layers.

As a matter of fact, it took a lot of time to arrive at some decisions especially regarding the implementation of the Eurocode 7. I more or less agree with the conclusions of Raisons (2017) regarding Eurocode 7 as follows;

1. EC7 does not tell the Designer how to design piles but does give rules and procedures to be followed
2. EC7 has complicated pile design with the introduction of numerous partial factors; load factors, combination factors, material factors, resistance factors, model factors and correlation factors
3. More design effort is required in EC7, and ultimately,
4. Engineering judgement cannot be suspended

Thanks for reading this post. You can contact the author via mail;

ubani@structville.com

To download this post as a PDF file, click HERE

References
[1] Wrana B. (2015): Pile Load Capacity – Calculation Methods. Studia Geotechnica et Mechanica, Vol. 37, No. 4, 2015 DOI: 10.1515/sgem-2015-0048
[2] Faseki O.E., Olatinpo O.A., Oladimeji, A.R. (2016): Assessment of Sub-Soil Geotechnical Properties for Foundation Design in Part of Reclaimed Lekki Pennisula, Lagos, Nigeria. International Journal of Advanced Structures and Geotechnical Engineering ISSN 2319-5347, Vol. 05, No. 04, October 2016
[3] Raison Chris (2017): Pile Design to BS EN 1997-1:2004 (EC7) and the National Annex. Raison Foster Associates, University of Birmingham, UK
[4] NAVFAC DM 7.2 (1984): Foundation and Earth Structures, U.S. Department of the Navy.
[5] EN 1997-1:2004:Geotechnical design – Part 1: General rules, European Committee for Standardization 
[6] Meyerhof,  G.G.  (1951):  The  ultimate  bearing  capacity  of  foundations,  Géotechnique,  2, 301-332 
[7] Warmate T. and Nwankwoala H. O. (2019): Geotechnical Indications and Shallow Bearing Capacity Analysis within Lekki Peninsula, Lagos using Direct Shear Analysis. Cur Trends Civil & Struct Eng. 1(4): 2019. http://dx.doi.org/10.33552/CTCSE.2019.01.000516