Structural Design of Steel Fin Plate Connection

1.0 Introduction
The fin plate connection is very popular in the construction industry due to its ease of erection, and the absence of shared bolts in two sided connections. It consists of a length of plate welded to the supporting member (eg column or primary beam), and the supported member bolted to the fin plate. Technically, fin plates derive their rotational capacity from shear deformation of the bolts, and hole distortion in the fin plate and/or the beam web.

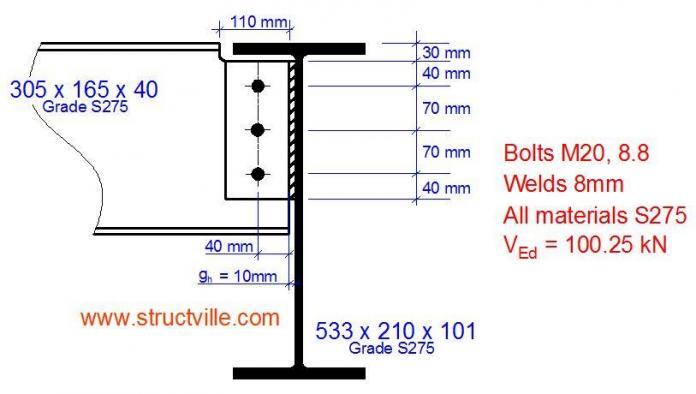
2.0 Practical Considerations and Recommended Geometry
With 10mm thick fin plate in S275 steel, 8mm fillet weld to the supporting member will guard against any possibility of weld failure (CSI, 2011). Fin plates may be classified as short or long as follows;

Short t_p/z_p ≥ 0.15
Long t_p/z_p < 0.15

Where z_p is the distance between the face of the support and the first line of bolts. For short fin plates, erection on site is usually more difficult, but with long fin plates, care must be taken against lateral torsional buckling, especially if the beam is laterally unrestrained.

According to SCI (2011), when detailing the joint, the following recommendations should be followed;
(1) Full strength fillet welds are provided
(2) The fin plate is positioned close to the top flange in order to provide positional restraint
(3) The depth of the fin plate is at least 0.6 times the supported beam depth in order to provide the beam with adequate torsional restraint
(4) The thickness of the fin plate or the beam web is ≤ 0.50d (for S275 steel)
(5) Property class 8.8 bolts non-preloaded are used
(6) All end and edge distances on the plate and the beam web are at least 2d

Since the depth of beam is less than 610mm, let us adopt fin plate size of 100 x 10mm
Gap g_h = 10mm
Bolt rows = 3
Length of plate = 0.6 × 303.4 = 182.04mm (provide plate length = 220mm)

(i) Supported beam Bolt Shear Check
Basic requirement V_Ed ≤ V_Rd

V_Rd = nF_v,Rd/sqrt[(1 + αn)² + (βn)²]

F_v,Rd = (α_vf_ubA)/γ_m2

For M20 8.8 bolts;
F_v,Rd = (0.6 × 800 × 245)/1.25 = 94080 N = 94.08 kN

For a single vertical line of bolt (n₂ = 1, and n = n₁); α = 0

β = 6z/[n₁(n₁ + 1)p₁]
β = (6 × 30)/[3 × (3 + 1) × 70] = 0.214

Therefore;
V_Rd = (3 × 94.08)/sqrt[(1 + 0 × 3)² + (0.214 × 3)²)] = 237.506 kN

V_Ed = 100.25 kN < 237.506 kN
Therefore bolt group is ok for shear

(ii) Fin plate in bearing
Basic requirement V_Ed ≤ V_Rd

V_Rd = n/sqrt{[(1 + αn)/(F_b,ver,Rd )]² + [βn/(F_b,hor,Rd]²}

α = 0; β = 0.214

The vertical bearing resistance of a single bolt
F_b,ver,Rd = (k₁α_bf_updt_p)/γ_m2

k₁ = min[2.8(e₂/d₀) – 1.7; 2.5) =  min[2.8(50/22) – 1.7; 2.5)
= min[4.66;2.5] = 2.5

α_b = min[e₁/3d₀; (p₁/3d₀ – 1/4); f_ub/f_up; 1.0]
= min[40/(3 × 22); (70/(3 × 22) – 0.25); 800/410; 1.0]
= min[0.61; 0.81; 1.95; 1.0] = 0.61

F_b,ver,Rd = (2.5 × 0.61 × 410 × 20 ×10)/1.25 = 100040 N = 100.04 kN

The horizontal bearing resistance of a single bolt
F_b,hor,Rd = (k₁α_bf_updt_p)/γ_m2

k₁ = min[2.8(e₁/d₀) – 1.7; 1.4(p₁/d₀) – 1.7;  2.5)
=  min[2.8(40/22) – 1.7; 1.4(70/22) – 1.7;2.5)
= min[3.39; 2.75; 2.5] = 2.5

α_b = min[e₂/3d₀; f_ub/f_up; 1.0]
= min[50/(3 × 22); 800/410; 1.0]
= min[0.76; 1.95; 1.0] = 0.76

F_b,hor,Rd = (2.5 × 0.76 × 410 × 20 ×10)/1.25 = 124640 N = 124.64 kN

V_Rd = (3)/sqrt{[(1 + 0 × 3)/100]² + [(0.214 × 3)/124.64]²) = 288.218 kN

V_Ed = 100.25 kN < 288.218 kN Ok

(iii) Supported Beam – Fin Plate

Shear
Basic requirement V_Ed ≤ V_Rd,min

V_Rd,min = min(V_Rd,g;V_Rd,n;V_Rd,n)

Gross section
V_Rd,g = (h_p.t_p.f_fy,p)/[1.27 × sqrt(3) × γ_m0]

V_Rd,g = [(220 × 10 × 275)/(1.27 × √3 × 1.0)] × 10^-3 = 275.034 kN

Net Section
V_Rd,n = A_v,net × [f_u,p / (sqrt(3) × γ_m2)]

Net Area = A_v,net =  t_p.(h_p – n₁.d₀)
A_v,net =  10(220 – 3 × 22) = 1540 mm²

V_Rd,n = 1540  × [410 / (√3 × 1.1)] × 10^-3 = 331.399 kN

Block Tearing
V_Rd,b = [(0.5f_u,p A_nt)γ_m2] +  [f_y,p A_nv / (sqrt(3) × γ_m0)]

Net area subject to tension = A_nt = t_p[e₂ –  0.5d₀]
A_nt = 10[e₂ –  0.5d₀]
A_nt = 10[50  –  0.5 × 22] = 390 mm²

Net area subject to shear = A_nv = t_p[h_p – e₁ –  (n₁ – 0.5)d₀]
A_nv = 10[20 – 40 –  (3 – 0.5) × 22] = 1250 mm²

V_Rd,b = [(0.5 × 410 × 390)1.1] +  [(275 × 1250)/ (sqrt(3) × 1.0)] = 72681.818 + 198464.155 = 271145.973 = 271.145 kN

V_Rd,min = min(275.034; 331.399; 271.145 ) = 271.145 kN

V_Rd,min = 100.25 kN < 271.145 kN Ok

Lateral Torsional Buckling of fin plates
Basic requirement V_Ed ≤ V_Rd
t_p/z_p = 220/50 = 4.4 > 0.15

Therefore fin plate is short;
V_Rd = [(W_el,p/z) × (f_y,p / γ_m0)]

W_el,p = (t_ph_p²)/6 = (10 × 220²)/6 = 73333.333 mm³

V_Rd = [(73333.333/50) × (275 / 1.0)] = 403333.333 N = 403.333 kN
V_Ed = 100.25 kN < 403.33 kN Ok

Supported Beam in Shear
Gross Section
V_Rd,g = [A_v,web × (f_y,b1  / (sqrt(3) × γ_m0))]

Gross Area A_v  = A_Tee – bt_f,b1 + (t_w,b1 + 2r_b1) × 0.5t_f,b1

A_Tee =  (265.2 – 10.2) × 6 + (165 × 10.2) = 1530 + 1683 = 3213 mm²
A_v  = 3213 – (165 × 10.2) +  (6 + 2 × 8.9) × 0.5 × 10.5 = 3213 – 1683 + 124.95 = 1654.95 mm²

V_Rd,g = 1654.95 × 275 / (sqrt(3) × 1.0) = 262758.603 N = 262.758 kN

Net Section
V_Rd,n = [A_v,net × (f_u,b1  / (sqrt(3) × γ_m2))]

Net area; A_v,net = A_v – n₁d₀t_w,b1 = 1654.95 – (3 × 22 × 6) = 1258.95 mm²

V_Rd,n = 1258.95 × 410 / (sqrt(3) × 1.1) = 270918.727 N = 270.918 kN

Block Tearing
V_Rd,b = [(0.5f_u,b1 A_nt)γ_m2] +  [f_y,b1 A_nv / (sqrt(3) × γ_m0)]

Net area subject to tension = A_nt = t_w,b1[e_2,b –  0.5d₀]
A_nt = 6[40  –  0.5 × 22] = 174 mm²

Net area subject to shear = A_nv = t_w,b1[e_1,b + (n₁ – 1)p₁ – (n₁ – 0.5)d₀]
A_nv = 6[40 + (3 – 1)70 –  (3 – 0.5)22] = 750 mm²

V_Rd,b = [(0.5 × 410 × 175)1.1] +  [(275 × 750)/ (sqrt(3) × 1.0)] = 35873.9 + 119081.986 = 154955.886 = 154.955 kN

V_Rd,min = min(262.758; 270.918; 154.955) = 154.955 kN

V_Rd,min = 100.25 kN < 154.955 kN Ok

Check for welding (supporting beam)
For a beam in S275 steel;

Basic requirement; a ≥ 0.5t_p
0.5t_p = 0.5 × 10 = 5mm
a = 5.7mm > 0.5t_p

Thank you for visiting Structville today. God bless you.