Design of Waffle Slabs

Waffle slabs are reinforced concrete slabs that are normally employed for large-span construction. They can be described as the equivalent of 2-way spanning solid slabs but with a ribbed slab system spanning in both directions. In waffle slabs, the grids run in two directions to provide support for the floor.

Waffle slabs have a flat top and a surface resembling a grid made of concrete joists on the bottom. After the concrete has set and cured, the waffle moulds are removed to create the grid. Due to the rigidity of the waffle slab, this form of structure is suggested for buildings like manufacturing plants and laboratories that require little vibration.

Additionally, waffle slabs are utilized in structures like theatres and train stations that call for expansive open areas. Waffle slabs may be more expensive than other types of slabs because they require intricate formwork, but depending on the project and the amount of concrete used, they may be less expensive to construct.

The design concept of waffle slabs is similar to that of ribbed slabs, with the difference being that waffle slabs have ribs spanning in both directions, and the coefficients used for analysing the slab are similar to those used for a two-way restrained slab. Waffle slabs are supported on beams or columns, where the support zones are made to be uniformly thick.

Design Example of Waffle Slab

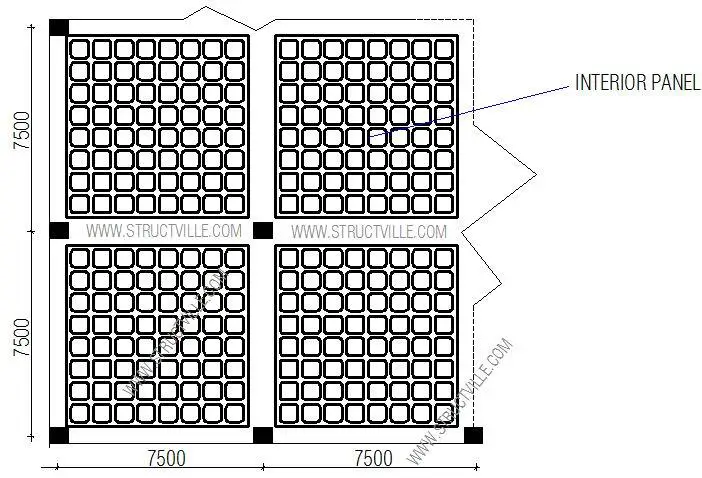
A church building has a square grid of 7.5m x 7.5m of waffle slab, and is to support an imposed load of 5 kN/m², design an interior panel of the waffle slab, and a supporting beam. f_ck = 30 Mpa, f_yk = 500 Mpa. The design will be done according to Eurocode 2 (EN 1992-1-1:2004).

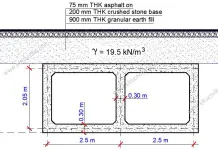
For details of waffle mould, see details of technical data sheet.

Solution
From basic span/effective depth ratio of 26, the trial depth of slab to be adopted = 7500/26 = 288 mm

From the table, let us select the following mould details;
Mould height = 225 mm
Top layer thickness = 75 mm
Total height of slab = 300 mm
Average rib width = 176 mm

Load Analysis
Self weight of concrete = 5.2 kN/m² (see technical data sheet)
Finishes = 1.2 kN/m²
Partition allowance = 1.5 kN/m²
Total permanent action = 7.9 kN/m²

Imposed load = 5 kN/m²

At ultimate limit state = 1.35g_k + 1.5q_k = 1.35(7.9) + 1.5(5) = 18.165 kN/m²

Load per rib = 0.9 × 18.165 = 16.35 kN/m²

Analysis of the slab
Treating as all sides fixed:
k = L_y/L_x = 1.0
Span coefficient = +0.024
Support coefficients = -0.032

Design of the span
Designing the span as a T-beam;
M_Ed =  0.024 × 16.35 × 7.5² = 22.07 kN.m

Effective depth (d) = h – C_nom – ϕ/2 – ϕ_links
Assuming ϕ12 mm bars will be employed for the main bars, and ϕ10 mm bars for the stirrups (links)
d = 300 – 25 – (12/2) -10 = 259 mm

k = M_Ed/(f_ckbd²) = (22.07 × 10⁶)/(30 × 500 × 259²) = 0.0219
Since k < 0.167, no compression reinforcement required

z = d[0.5+ √(0.25 – 0.882k)]
k’ = 0.0219
z = d[0.5+ √((0.25 – 0.882(0.0219))] = 0.95d = 246.05 mm

Depth to neutral axis x = 2.5(d – z) = 2.5(259 – 246.05) = 32.375 mm < 1.25h_f (93.75 mm)
Therefore, we design rib as a rectangular section

Area of tension reinforcement A_s1 = M_Ed / (0.87f_yk z)
A_s1 = M_Ed / (0.87f_yk z) = (22.07 × 10⁶) / (0.87 × 500 × 0.95 × 259) = 206 mm²

Provide 2H12  Bot (A_Sprov = 226 mm²)

Check for deflection
ρ = A_s,req /bd = 206 / (900 × 259) = 0.0008837
ρ₀ = reference reinforcement ratio = 10^-3√(f_ck) = 10^-3√(30) = 0.00547
Since  ρ ≤ ρ₀;
L/d = k [11 + 1.5√(f_ck) ρ₀/ρ + 3.2√(f_ck) (ρ₀/ρ – 1)^(3⁄2)]
k = 1.5 (continuous system)
L/d = 1.5 [11 + 1.5√(30) × (0.00547/0.0008837) + 3.2√(30) × [(0.00547 / 0.0008837) – 1]^(3⁄2)]
L/d = 1.5[11 + 50.855 + 207.227] = 269.082

β_s = (500 As_prov)/(f_yk As_req) = (500 × 226) / (500 × 206) = 1.09

b_eff/b_w = 900/176 = 5.11

Therefore multiply basic length/effective depth ratio by 0.8

Therefore limiting L/d = 1.09 × 0.8  × 269.082 = 234.639
Actual L/d = 7500/259 = 28.96

Since Actual L/d (28.96) < Limiting L/d (234.639), deflection is satisfactory.

Design of Supports;
M_Ed = 0.032 × 16.35 × 7.5² = 29.43 kN.m

k = M_Ed/(f_ckbd²) = (29.43 × 10⁶)/(30 × 176 × 259²) = 0.083
Since k < 0.167, no compression reinforcement required

z = d[0.5+ √(0.25 – 0.882k)]
k = 0.083
z = d[0.5+ √((0.25 – 0.882(0.083))] = 0.92d

Area of tension reinforcement A_s1 = M_Ed / (0.87f_yk z)
A_s1 = M_Ed / (0.87f_yk z) = (29.43 × 10⁶) / (0.87 × 500 × 0.92 × 259) = 283 mm²
Provide 3H12 TOP (A_Sprov = 339 mm²)

Shear Design 
Maximum shear force in the rib 
V_Ed = 0.33 × 16.35 × 7.5 = 40.466 kN/m

V_Rd,c = [C_Rd,c.k.(100ρ₁ f_ck)^(1/3) + k₁.σ_cp]b_w.d ≥ (V_min + k₁.σ_cp) b_w.d

C_Rd,c = 0.18/γ_c = 0.18/1.5 = 0.12
k = 1 + √(200/d) = 1 + √(200/259) = 1.88 < 2.0, therefore, k = 1.88
V_min = 0.035k^(3/2) f_ck^0.5
V_min = 0.035 × (1.88)^1.5 × 30^0.5 = 0.494 N/mm²
ρ₁ = As/bd = 339/(176 × 259) = 0.00743 < 0.02; Therefore take 0.00743

V_Rd,c = [0.12 × 1.88 (100 × 0.00743 × 30 )^(1/3)] × 176 × 259 = 28941.534 N = 228.94 kN

Since V_Rd,c (28.94 kN) < V_Ed (40.466 kN), shear reinforcement is required.
The compression capacity of the compression strut (V_Rd,max) assuming θ = 21.8° (cot θ = 2.5)

V_Rd,max = (b_w.z.v₁.f_cd) / (cot⁡θ + tanθ)
V₁ = 0.6(1 – f_ck/250) = 0.6(1 – 30/250) = 0.528
f_cd = (α_cc f_ck) / γ_c = (0.85 × 30) / 1.5 = 17 N/mm²
Let z = 0.9d

V_Rd,max = [(176 × 0.9 × 259 × 0.528 × 17) / (2.5 + 0.4)] × 10^-3 = 126.981 kN

Since < V_Ed < V_Rd,c < V_Rd,max

Hence A_sw / S = V_Ed / (0.87 F_yk z cot θ) = 40466 / (0.87 × 500 × 0.9 × 259 × 2.5 ) = 0.159

Minimum shear reinforcement;
A_sw / S = ρ_w,min × b_w × sinα (α = 90° for vertical links)
ρ_w,min = (0.08 × √(f_ck)) / f_yk = (0.08 × √30) / 500 = 0.000876
A_sw/S_min = 0.000876 × 176 × 1 = 0.154
Maximum spacing of shear links = 0.75d = 0.75 × 259 = 194.25 mm

Provide H8mm @ 175 mm c/c as shear links (A_sw / S = 0.574)

Slab Topping
A142 BRC Mesh can be provided or H8 @ 250mm c/c

Watch out for design of supporting beams…