Design of Shear Walls

Shear walls are structural members that provide additional lateral stiffness to a building by resisting shear, moment, and axial forces, which are produced due to gravity and lateral loads. In some design cases, the entire lateral loads coming to a building assumed to be resisted by shear walls alone, especially when it is the major stabilising/bracing component of the building. The design of shear walls involves providing adequate cross-section and reinforcements to resist bending, shear, axial, and twisting forces due to gravity and lateral loads.

For an element to be described as a reinforced concrete wall, the length to thickness ratio should be equal to or greater than 4 (Clause 9.6.1, Eurocode 2). A shear wall is said to be short when the height-to-width ratio is less than or equal to one, while it is said to be slender when the height-to-width ratio is greater than or equal to four. For slender walls, bending deformation is dominant, while in short walls, shear deformation is dominant. When the height-to-width ratio is in-between one and four, then the shear wall undergoes both shear and bending deformations.

Forces Acting on Shear Walls

Shear walls are designed to resist bending moment, shear, axial, and uplift forces, especially when they are subjected to lateral actions. The lateral forces acting in the plane of a shear wall attempts to lift up one end of the wall and push the other end down. Uplift forces are greater on tall walls and less on low walls. Shear walls resist the shear force parallel to the plane of the wall by cantilever action.

Axial forces in a Shear wall
The axial load in a wall may be calculated assuming the beams and slabs transmitting the loads to it are simply supported.

Transverse moments
For continuous construction, transverse moments can be calculated using elastic analysis. The eccentricity is not to be less than h/30 or 20 mm where h is the wall thickness.

In-plane moments
Moments in the plane of a single shear wall can be calculated from statics. When several walls resist forces, the proportion allocated to each wall should be in proportion to its stiffness.

Location/Placement of Shear of Shear Walls

In a tall building where the shear wall is used for lateral stability, it should be located on each level of the structure. Preferably, shear walls of equal length should be placed symmetrically on all four exterior walls of the building to form an effective box structure. When the shear walls in the exterior frame could not provide sufficient strength and stiffness, the shear walls should be added to the interior frame as well.

If the shear wall is placed at the interior frame of a building, it attracts and resists higher internal forces but may not be too effective in reducing the maximum lateral deflection of the building. However, if a shear wall is placed at the ends of a building, the lateral deflection is reduced considerably when compared to the later.

Architectural disposition in a building may not always give the room for optimum placement of shear walls for good structural performance. In some areas such as lift areas or window/door openings, coupled shear walls may have to be used. However, the best position or arrangement of shear walls in a building is a symmetrical arrangement whereby the shear centre (centre of rotation) will coincide with the centre of gravity of the building in order to reduce or eliminate torsion (twisting) due to lateral loads.

Functions of Shear Walls

• Shear walls must provide the necessary lateral strength to resist horizontal wind and earthquake forces.
• They provide resistance against sliding through connections.
• They also provide lateral stiffness to prevent the roof or floor above from excessive side sway.
• When the shear walls are stiff enough, they prevent floor and roof framing members from moving off their supports.
• Buildings that are sufficiently stiff usually suffer less structural damage due to the presence of shear walls.

Structural Action of a Shear Wall

In a shear wall, the primary mode of deformation is mainly due to flexure but not shear. The mode of deformation of shear walls is such that it has maximum slope at the top and least at the bottom which is the flexural mode shape. The structural action of a shear wall resembles that of a cantilever beam.

Structural Design of Shear Walls

The amount of reinforcement needed for proper detailing of a reinforced concrete wall may be derived using strut-and-tie model. If a wall is however subjected predominantly to out-of-plane bending, the design rules and guidelines for slabs apply. In Eurocode 2, the requirements for the design of columns and shear walls are not so different except in the following areas;

■ The requirements for fire resistance
■ Bending will be critical about the weak axis
■ Rules for spacing and quantity of reinforcement

Reinforcement Detailing of Shear Walls

(a) Minimum and maximum area of vertical reinforcement
According to clause 9.6.2 of Eurocode 2, the minimum and maximum amounts of reinforcement required for a reinforced concrete wall are 0.002A_c and 0.04A_c outside lap locations respectively. It is further stated that where minimum reinforcement controls design, half of this area should be located on each face. The distance between two adjacent vertical bars should not exceed three times the wall thickness or 400 mm, whichever is lesser.

(b) Area of horizontal reinforcement
According to clause 9.6.3 of Eurocode 2, horizontal reinforcement should be provided at each face and should have a minimum area of 25% of the vertical reinforcement or 0.001A_c, whichever is greater. The spacing between two adjacent horizontal bars should not be greater than 400 mm.

(c) Provision of links
If the compression reinforcement in the wall exceeds 0.02A_c, links must be provided through the wall thickness in accordance with the rules for columns in clause 9.5.3 which are:

The diameter of the transverse reinforcement should not be less than 6 mm or one-quarter of the diameter of the largest longitudinal bar whichever is greater. The maximum spacing is to be S_{cl, max}

S_{cl, max} is the minimum of;

• 20 times the diameter of the smallest longitudinal bar
• The lesser dimension of the wall i.e. the thickness
• 400 mm

The maximum spacing should be reduced by a factor of 0.6 in the following cases;

• In sections within a distance equal to 4 × thickness of wall above or below a beam or slab.
• Near lapped joints, if the diameter of the longitudinal bar is greater than 14 mm. A minimum of three bars evenly placed in the lap length is required.

Where the main reinforcement (i.e., vertical bars) is placed nearest to the wall faces, transverse reinforcement should be provided in the form of links with 4 per m² of the wall area.

Design Example of Shear Walls

Design a 225 mm thick shear wall of 3.6 m height at the ground floor of the building. The shear wall is carrying a 200 mm thick slab on the first floor of the building. The action effects on the shear wall are as follows;

Vertical loads
Dead Load G_k = 300 kN/m
Live load Q_k = 55 kN/m

Vertical load due to in-plane bending and wind W_k = ±650 kN/m
Vertical load due to in-plane bending and imperfections G_kH = ±60 kN/m

Maximum moment out-of-plane, floor imposed load as leading action M = 40 kN/m @ ULS
Maximum moment out-of-plane, floor imposed load as accompanying action M = 35 kN/m @ ULS

f_ck = C25/30; f_yk = 500 N/mm²

Check slenderness of wall at ground floor

Effective length, l₀ = 0.75 × (3600 – 200) = 2550 mm (Table C16)
λ = 3.46 × l₀/h = 3.46 × 2550/225 = 39.213 (Cl. 5.8.3.2(1))

Limiting slenderness, λ_lim = 20 ABC/n^0.5 (Cl. 5.8.3.1(1))
where;
A = 0.7
B = 1.1
C = 1.7 – r_m

where;
r_m = M₀₁/M₀₂ = say = –0.25
C = 1.7 – (-0.25) = 1.95
n = N_Ed/A_cf_d

where;
N_Ed (assuming wind is the leading variable action) = 1.35G_k + 1.5Q_k1 + 1.5Ψ₀Q_ki
= 1.35(300 + 60) + 1.5(650) + (1.5 × 0.7 × 55) = 486 + 975 + 57.75 = 1518.75 kN/m
A_cf_d = (225 × 1000) × (0.85 × 30/1.5) = 3825 kN
Therefore, n = 1518.75/3825 = 0.397
λ_lim = 20 ×( 0.7 × 1.1 × 1.95)/0.397^0.5 = 47.66

Therefore as λ < λ_lim wall is not slender and therefore no secondary moments.

Combinations of actions
(a) At ULS, for maximum axial load, W_k is leading variable action
N_Ed = 1.35G_k + 1.5Q_k1 + 1.5Ψ₀Q_ki
= 1.35(300 + 60) + 1.5(650) + (1.5 × 0.7 × 55) = 486 + 975 + 57.75 = 1518.75 kN/m

M_Ed = M + e_iN_Ed ≥ e₀N_Ed (Cl. 5.8.8.2(1), 6.1.4)

where
M = moment from 1st order analysis = 35 kNm/m
e_i = l₀/400 = 2550/400 = 6.375 mm (Cl. 5.2(7), 5.2(9))
e₀ = h/30 ≥ 20 mm = 20 mm (Cl. 6.1.4)

M_Ed = 35 + (0.006375 × 1518.75) ≥ 0.020 × 1518.75
M_Ed = 35 + 9.68 ≥ 30.375 = 44.68 kNm/m

(b) At ULS, for minimum axial load, W_k is leading variable action
N_Ed = (1.0 × 300) – (1.35 × 60) – (1.5 × 650) + (0 × 55) = –756 kN/m (tension)

M_Ed = 35 + (0.006375 × 756) ≥ 0.020 × 756
= 35 + 4.82 ≥ 15.12 = 39.82 kNm/m

(c) At ULS, for maximum out of plane bending assuming Q_k is leading variable action

N_Ed = 1.35(300 + 60) + (1.5 × 55) + (1.5 × 0.5 × 650) = 1056 kN/m

M_Ed = 40 + (0.006375 × 1056) ≥ 0.020 × 1056
M_Ed = 40 + 6.732 ≥ 21.12 = 46.732 kNm/m

or

N_Ed = (1.0 × 300) – (1.35 × 60) – (0 × 55) – (1.5 × 0.5 × 650) = -268.5 kN/m (tension)
M_Ed = 40 + (0.006375 × 268.5) = 41.71 kNm/m

Design load cases
Consolidate (c) into (a) and (b) to consider two load cases:

N_Ed = 1518.75 kN/m
M_Ed = 46.732 kNm/m (out of plane)

and

N_Ed = –756 kN/m (tension)
M_Ed = 46.732 kNm/m (out of plane)

Design: cover above ground
c_nom = c_min + ∆c_dev

where;
c_min = max[c_min,b; c_min,dur] (Exp. (4.1))

where
c_min,b = diameter of bar = 20 mm vertical or 10 mm lacers
c_min,dur = for XC1 = 15 mm
∆c_dev = 10 mm
c_nom = 15 + 10 = 25 mm to lacers (35 mm to vertical bars)

Design using charts
For compressive load:
d₂/h = (25 + 10 + 16/2)/225 = 0.19

Interpolate between charts for d₂/h = 0.15 and d₂/h = 0.2 as shown below

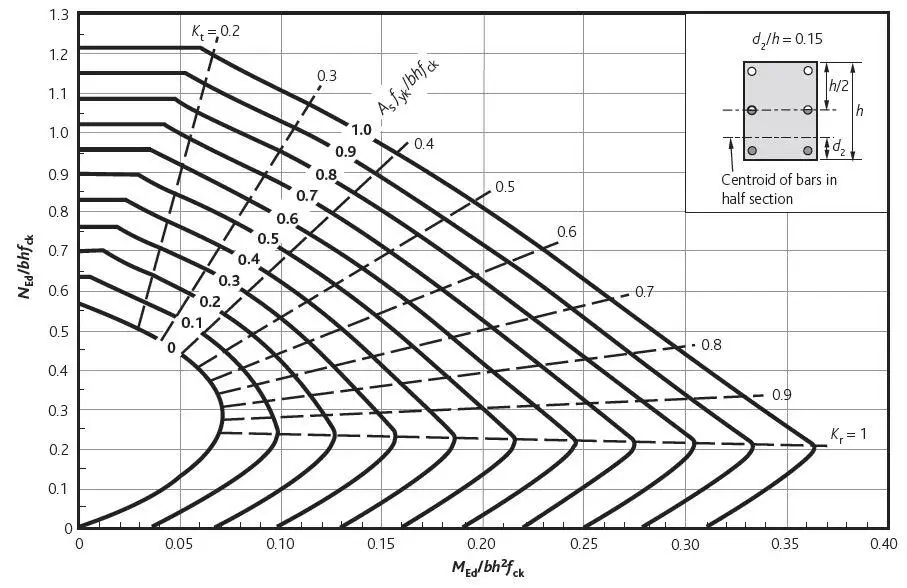
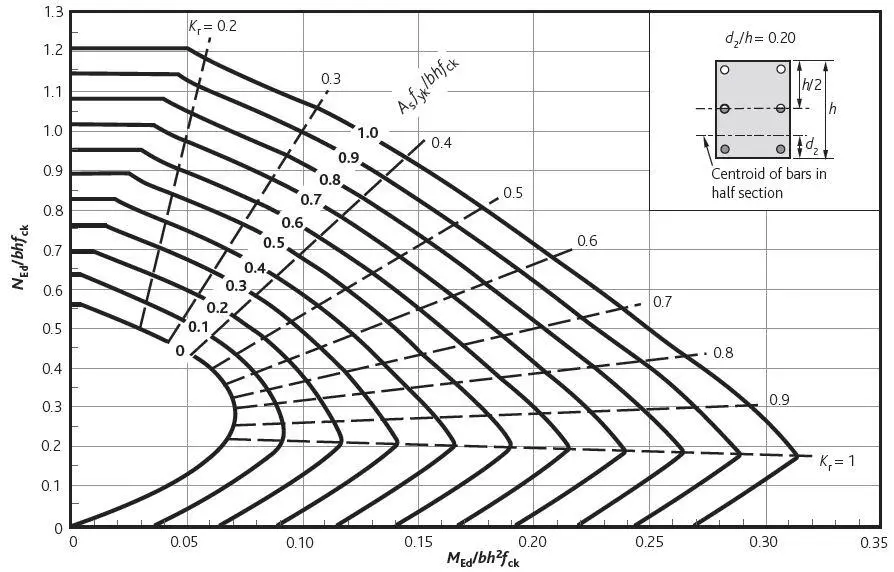
N_Ed/bhf_ck = (1518.75 × 10³)/(225 × 1000 × 30) = 0.225
M_Ed/bh²f_ck = (46.732 × 10⁶)/(225² × 1000 × 30) = 0.030

Gives:A_sf_yk/bhf_ck = 0
Therefore, minimum area of reinforcement required

A_s,min = 0.002A_c (Cl. 9.6.2 & NA)
A_s,min = 0.002 × 225 × 1000 = 450 mm²/m
A_s,min = 450 mm²/m = 225 mm²/m each face
maximum spacing = 400 mm c/c, minimum diameter of rebar = 12 mm diameter

Try H12 @ 300 c/c on each face

For tensile load and moment
Working from first principles, referring to the figure below and ignoring contribution from concrete in tension,

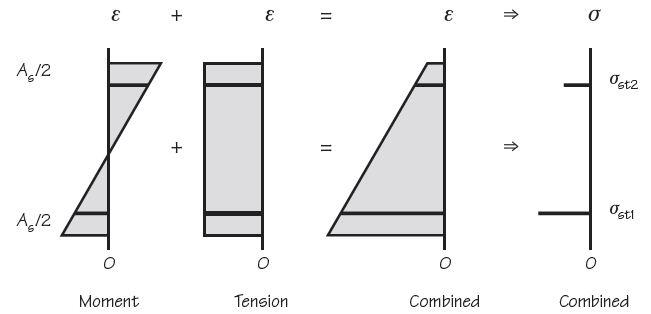
N_Ed = (σ_st1 + σ_st2) × A_s/2
and M_Ed = (σ_st1 – σ_st2) × A_s/2 × (d – d₂)

So σ_st1 + σ_st2 = 2N_Ed/A_s
and σ_st1 – σ_st2 = 2M_Ed/[(d – d₂)A_s]

2σ_st1 = 2N_Ed/A_s + 2M_Ed/[(d – d₂)A_s]
As = (N_Ed/σ_st1) + M_Ed/(d – d₂)σ_st1

σ_st1 = f_yk/γ_s = 500/1.15 = 434.8

A_s = (756 × 10³/434.8) + (46.732 × 10⁶)/[(182 – 43) × 434.8] = 1738.7 + 773 = 2512 mm²

σ_st2 = 2N_Ed/A_s – σ_st1 = 601.9 – 434.8 = 167 MPa

By inspection all concrete is in tension zone and may be ignored.
Use 7H16 @ 175 c/c on both sides for at least 1 m each end of wall (A_sprov = 2814 mm²).

Horizontal reinforcement
A_s,hmin = 0.001A_c or 25% A_s,vert (Cl. 9.6.3(1) & NA)
= 225 mm² or (0.25 × 2814) = 704 mm²/m
This therefore requires 352 mm²/m each side
Use H10 @ 200 (393 mm²/m) both sides

Links
Check 0.02A_c = 0.02 × 225 × 1000 = 4500 mm² > 2814 mm²
Therefore, links not required.
.