Foundations can be subjected to dynamic loads in addition to static loads in engineering practice. Dynamics loads can be found in pile foundations supporting machines, oil and gas facilities, buildings under seismic effect, wind turbines, etc. The design of foundations under dynamic loading is complex and involves the inputs of structural, mechanical, and geotechnical engineering, as well as the theory of vibration.
In some cases, using deep foundations rather than shallow foundations may be required for foundations subjected to dynamic loads. Many factors influence whether a structure should be supported on a shallow or deep foundation system, including subsurface conditions and induced dynamic and static stresses.
Pile foundations are utilized to prevent bearing capacity failure, improve the system’s dynamic stiffness, and reduce dynamic oscillations. However, when a complete understanding of the dynamic interaction between the pile and the soil (pile-soil interaction) and between adjacent piles (pile-soil-pile interaction) is necessary, calculations become more difficult.

In general, applying dynamic loads to piles in cohesive soils reduces their skin friction and end-bearing value, i.e., reduces their ultimate carrying capacity, whereas applying dynamic loads to piles in granular soils reduces their skin friction but increases their end-bearing resistance at the expense of increased settlement under working load (Tomlinson, 1994).
The reduction in skin friction and end-bearing resistance of piles in cohesive soils is due to cyclic loading reducing the shearing strength of these soils. The ratio of the applied stress to the ultimate stress of the soil determines the amount of decrease for an infinite number of load repetitions.
Novak (1974) proposed an approximate method for simulating the dynamic interaction between soil and single piles. His method presupposed that the soil is made up of a series of infinitesimally thin horizontal strata that extend indefinitely. As a result, it can be seen as a generic Winkler medium with inertia and the ability to dissipate energy. Novak’s work was able to establish the value of geometric damping, in addition to being more precise than earlier attempts.
Novak and AboulElla (1978) modified this approach to include the effect of having a soil profile that changes with depth. Novak and Sheta (1982) also incorporated the effect of the weak zone around the pile, which can be used to represent either soil-pile interface slippage or the real weak zone generated around the pile during construction.
All of these investigations reveal that frequency has a considerable impact on single pile dynamic impedance characteristics. Field tests (Manna and Baidya, 2009; Elkasabgy et al, 2010) have also corroborated this effect. As a result of soil non-linearity, field investigations on large-scale piles have also revealed a non-linear dynamic pile reaction.
Dynamic Behaviour of Single Piles
Khalil et al (2019) carried out numerical and experimental modelling on the dynamic behaviour of piles. In the study, a range of excitation frequencies ranging from 10Hz to 60Hz was considered in order to verify their effects on the dynamic behaviour of single piles. Under vertical and horizontal vibrations, the finite element model from the study reveals that as the excitation frequency increases, the stiffness Ks increases and the damping Cs reduces (see Figure 2).
The study found out that stiffness increased by 64% (under vertical vibrations) and by 120% (under horizontal vibrations) when the frequency is increased from 10 Hz to 60 Hz (a 500% increase). Damping, on the other hand, is reduced by 40% under vertical vibrations and by 26% under horizontal vibrations. These findings show that the excitation frequency affects the dynamic pile-soil interaction.
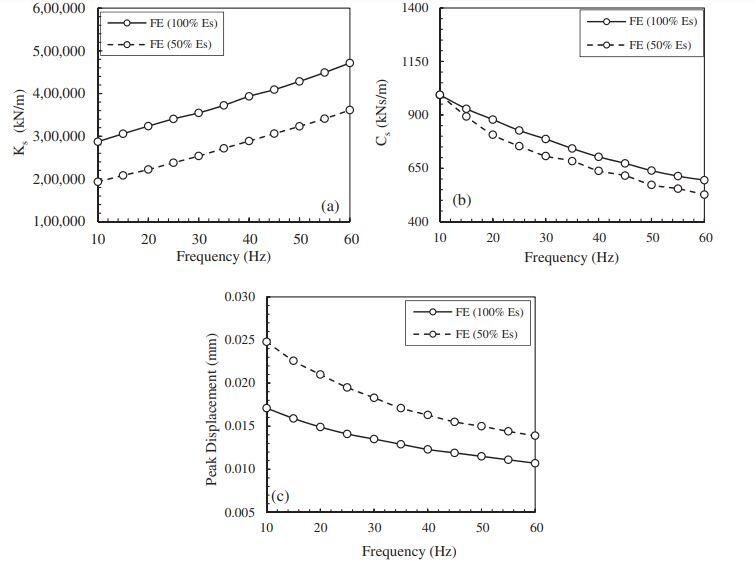
The effect of varying soil stiffness (Es) was also investigated in the study. When the value of soil stiffness was reduced by 50%, the numerical model revealed a corresponding drop in the impedance parameters of up to 33% for the stiffness and 12% for the damping (under vertical vibrations). For horizontal vibrations, this was up to 43% for stiffness and 27% for damping.
As a result, peak displacements can rise by 30 to 45% under vertical vibrations and 54 to 79% under lateral vibrations. This is to be expected, because lowering the soil stiffness lowers the soil resistance around the pile, resulting in a reduction in system stiffness and damping.
The slenderness ratio (L/D) of single piles subjected to vertical or lateral vibrations has no significant effect on their dynamic behavior. Peak displacements are reduced by less than 10% (under vertical vibrations) and 3% (under horizontal vibrations) when the pile slenderness ratio is increased from 20 to 30. This is consistent with the findings of Novat (1974) which show that raising the slenderness ratio has little effect on long flexible piles, especially when subjected to lateral motion. This happens because, regardless of the pile’s entire length, the soil mass contributing to the system’s dynamic resistance is confined to a specific depth.
Dynamic Behaviour of Piles in Group
Khalil et al. (2019) investigated the dynamic behavior of pile groups using a 3D finite element model. According to the findings, the group stiffness Kg increases at a variable rate as the frequency increases (see Figure 3). However, the group damping Cg increased significantly till it reaches f = 30 Hz to 40 Hz and decreased again after this point. Furthermore, the peak displacement reduced until it is nearly constant beyond 45 Hz. The study found that a pile group’s response is more sensitive to frequency than a single pile’s response.
The finite element model from the study showed a non-uniform drop in Kg as a result of lowering the soil stiffness (Es) by 50%. The reduction varies from as low as 4% (between 25 and 35 Hz) to as high as 39% at f = 60 Hz under vertical vibrations. Meanwhile, between 10 and 27 Hz, Cg slightly increased (by less than 5%). It however dropped by up to 39% for frequencies greater than 27 Hz.
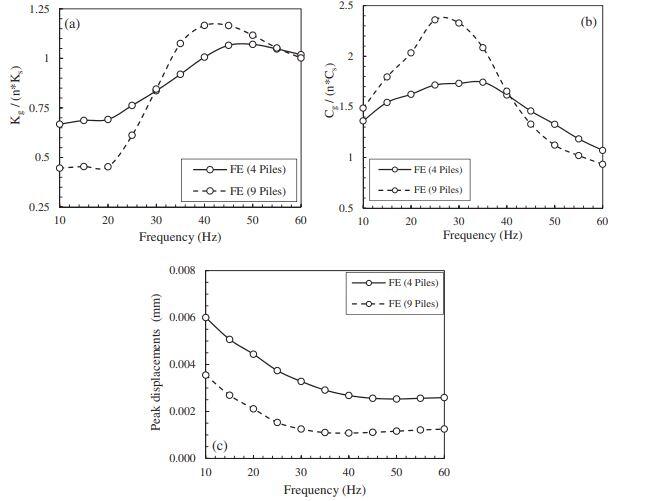
An overall rise in peak displacements was observed for the pile groups. However, this increase is inconsistent over the frequency range investigated, ranging from 8% to 52%. The reduction under lateral vibrations varies from as low as 24% at f = 35 Hz to as high as 42% at f = 60 Hz. In the meantime, the Cg drops by up to 35%. As a result, there was an overall rise in peak displacements.
Under vertical vibrations, the effect of modifying the dimensionless spacing ratio (S/D = distance between piles/pile diameter) was investigated using values of 3, 5, and 10 for a pile group of four. The phase at which the stress waves reach the adjacent vibrating piles changes as the spacing between piles increases. The stress waves become in-phase or out-of-phase with the vibrating nearby piles as a result of this change, which might cause the impedance parameters to reduce or rise.
The pile slenderness ratio (L/D) has a minor effect on the dynamic behavior of a pile group subjected to vertical or lateral vibrations, according to the research. Peak displacements are reduced by less than 5% (under vertical vibrations) and less than 7% (under horizontal vibrations) when the pile slenderness ratio is increased from 20 to 30. (under lateral vibrations).
Design of Pile Foundation under Dynamic Loading
To accommodate for dynamic load application on piles, it is common practice to double the safety factor on the combined skin friction and end bearing. The lateral loading of supporting piles can be caused by the torque of rotating machinery. The approaches can be used to determine the deflection under lateral loading in accordance with established methods. The deflections computed for the comparable static load should be doubled to account for dynamic loading.
The type of pile used, whether driven, driven-and-cast-in-place, or bored-and-cast-in-place, has no impact on the behavior of piles founded entirely in cohesive soils. Because of the development of an enlarged hole around the upper part of the shaft, lateral movements of piles with driven pre-formed shafts (e.g. precast concrete or steel H-piles) may be greater than those of cast-in-place piles (Tomlinson, 1994).
In granular soil, a pile’s skin-frictional resistance to static compressive force is quite low. When the pile is subjected to vibratory stress, this resistance is further reduced, and it is best to discard all frictional resistance on piles carrying high-frequency vibrating loads. If such piles are ended in loose to medium-dense soils, the settlement will continue to an unsatisfactory level for most machinery installations.
As a result, piles must be driven to a dense or very dense granular soil stratum, and even then, settlements can be large, especially if large end-bearing pressures are used. This is due to the soil grains’ increasing attrition at their places of contact. The slow but steady settlement of the piles is caused by the continued deterioration of the soil particles. Piles supporting vibrating machinery should, if possible, be driven completely through a granular soil stratum and terminate on bedrock or within a firm clay.
References
Elkasabgy M, El Naggar MH., and Sakr M. (2010): Full-scale vertical and horizontal dynamic testing of a double helix screw pile. Proc. of the 63rd Canadian Geotech; Conf., Calgary, Canada; 2010, pp. 352–359.
Khalil M. M., Hassan A. M., and Elmamlouk H. H. (2019): Dynamic behavior of pile foundations under vertical and lateral vibrations. HBRC Journal, 15(1):55-71, DOI: 10.1080/16874048.2019.1676022
Novak M. (1974): Dynamic stiffness and damping of piles. Can Geotech J. 11:574–598.
Novak M. and Aboul-Ella F (1978): Impedance functions for piles embedded in layered medium. J Eng Mech ASCE. 104(3):643–661.
Novak M. and Sheta M. (1982): Dynamic response of piles and pile groups. 2nd International Conference on Numerical Methods in Offshore Piling; Austin, TX; 1982.
Manna B and Baidya DK. (2009): Vertical vibration of full-scale pile—analytical and experimental study. J Geotech Geoenviron Eng. 135(10):1452–1461.
Tomlinson M. J. (1994): Pile Design and Construction Practice. E & FN SPON, London, UK










