Structural Design of Cantilever Beams

Cantilever beams are beams that are free at one end and rigidly fixed at the other end. Beams that are free at one end and continuous through the other support (beams with overhangs) are also treated as cantilever beams. The primary design of cantilever beams involves the selection of an adequate cross-section and reinforcements to resist the internal stresses due to the applied loads and to limit the deflection to an acceptable minimum.

Due to the structural system of cantilever beams, they are very sensitive to deflection and vibration. When loaded, the maximum shear force and bending moment occur at the fixed support, while the maximum deflection occurs at the free end. As a result, under normal circumstances in reinforced concrete design, the length of cantilevers is usually kept to a minimum in order not to have bulky sections and heavy reinforcements. In order to save material and to reduce the load due to self-weight, cantilever beams can be tapered, increasing linearly from the free end to the fixed support.

For cantilever beams, the tensile moment occurs at the top, therefore the main reinforcements are provided at the top. At the bottom, standard beam detailing requirements recommend that at least 50% of the reinforcement provided at the top be provided at the bottom. The anchorage length of the top reinforcement is expected to enter at least 0.25 times the effective span of the backspan or 1.25 times the effective length of the cantilever (whichever is greater).

A cantilever beam relies on the backspan or an alternative counterweight for equilibrium or structural stability.

Design Example of a Cantilever Beam

Design a two-span cantilever beam (beam with overhang with the following information provided). The beam is to support a rendered 230 mm hollow block wall up to a height of 2.7m, in addition to the load transferred by the floor slab. The ultimate design load on the slab is 12 kN/m². f_ck = 25 N/mm²; f_yk = 500 N/mm²; Concrete cover = 35mm; Unit weight of concrete = 25 kN/m³; Unit of block wall = 3.5 kN/m²

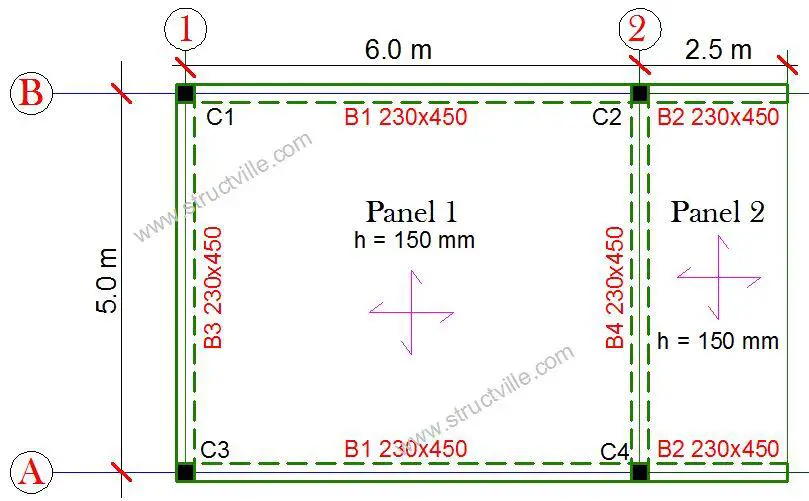
Load Analysis

Aspect ratio of the slab k = L_y/L_x = 6/5 = 1.2
Factored load transferred from slab to beam B1 = 0.5(12 × 5) × [1 – 0.333(1.2)²] = 15.61 kN/m
Factored load transferred from slab to beam B2 (factored) = γ_Gnl_x/4 = 1.35 × (12 × 2.5)/4 = 10.125 kN/m
Factored self-weight of the beam (considering the 300 mm drop) = 1.35(25 × 0.3 × 0.23) = 2.33 kN/m
Factored weight of block wall = 1.35(3.5 × 2.7) = 12.76 kN/m

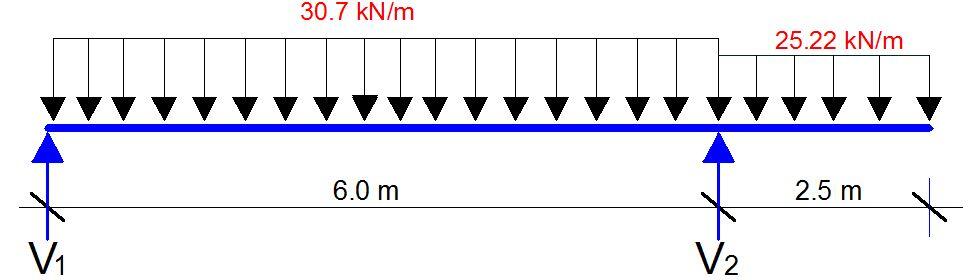
Load on Beam B1 = 15.61 + 2.33 + 12.76 = 30.7 kN/m
Load on neam B2 = 10.125 + 2.33 + 12.76 = 25.22 kN

Concrete details – Strength and deformation characteristics for concrete

Concrete strength class; C25/30
Aggregate type; Quartzite
Aggregate adjustment factor – cl.3.1.3(2);  AAF = 1.0
Characteristic compressive cylinder strength; f_ck = 25 N/mm²
Mean value of compressive cylinder strength; f_cm = f_ck + 8 N/mm² = 33 N/mm²
Mean value of axial tensile strength; f_ctm = 0.3 N/mm² × (f_ck/ 1 N/mm²)^2/3 = 2.6 N/mm²
Secant modulus of elasticity of concrete; E_cm = 22 kN/mm² × [f_cm/10 N/mm²]^0.3 × AAF = 31476 N/mm²

Ultimate strain – Table 3.1; ε_cu2 = 0.0035
Shortening strain – Table 3.1; ε_cu3 = 0.0035
Effective compression zone height factor; λ = 0.80
Effective strength factor; η = 1.00
Coefficient k₁; k₁ = 0.40
Coefficient k₂; k₂ = 1.0 × (0.6 + 0.0014 / ε_cu2) = 1.00
Coefficient k₃; k₃ = 0.40
Coefficient k₄; k₄ = 1.0 × (0.6 + 0.0014 / ε_cu2) = 1.00

Partial factor for concrete -Table 2.1N; γ_C = 1.50
Compressive strength coefficient – cl.3.1.6(1); α_cc = 0.85
Design compressive concrete strength – exp.3.15; f_cd = α_cc × f_ck / γ_C = 14.2 N/mm²
Compressive strength coefficient – cl.3.1.6(1); α_ccw = 1.00
Design compressive concrete strength – exp.3.15;   f_cwd = α_ccw × f_ck / γ_C = 16.7 N/mm²
Maximum aggregate size; h_agg = 20 mm
Monolithic simple support moment factor; β₁ = 0.25

Reinforcement details

Characteristic yield strength of reinforcement; f_yk = 500 N/mm²
Partial factor for reinforcing steel – Table 2.1N; γ_S = 1.15
Design yield strength of reinforcement; f_yd = f_yk / γ_S = 435 N/mm²

Nominal cover to reinforcement

Nominal cover to top reinforcement; c_{nom_t} = 35 mm
Nominal cover to bottom reinforcement; c_{nom_b} = 35 mm
Nominal cover to side reinforcement; c_{nom_s} = 35 mm

Fire resistance

Standard fire resistance period; R = 60 min
Number of sides exposed to fire; 3
Minimum width of beam – EN1992-1-2 Table 5.5; b_min = 120 mm

Flexural Design of the Cantilever Section

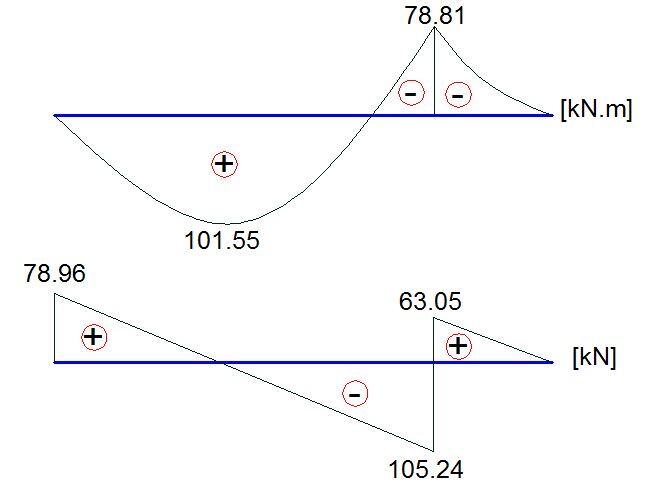
Design bending moment; M_Ed = 78.8 kNm

Distance between points of zero moment;  L₀ = (0.15 × L_{m1_s1}) + L_{m1_s2} = (0.15 × 6000) + 2500 = 3400 mm
Maximum flange outstand; b₁ = b_f – b = 720 mm
Effective flange outstand;  b_eff,1 = min(0.2 × b₁ + 0.1 × L₀; 0.2 × L₀; b₁) = 484 mm
Effective flange width; b_eff =  b_eff,1 + b = 714 mm
Effective depth of tension reinforcement; d = 399 mm

K = M / (b_eff × d² × f_ck) = 0.028

K’ = (2 × η × α_cc / γ_C) × (1 – λ × (δ – k₁) / (2 × k₂)) × (λ × (δ – k₁) / (2 × k₂)) = 0.207
Lever arm;  z = min(0.5 × d × [1 + (1 – 2 × K / (η × α_cc / γ_C)^0.5], 0.95 × d) = 379 mm
Depth of neutral axis;  x = 2 × (d – z) / λ = 50 mm

λx < h_f – Compression block wholly within the depth of flange
K’ > K – No compression reinforcement is required

Area of tension reinforcement required; A_s,req = max(M / (f_yd × z), A_s,min) = 478 mm²

Tension reinforcement provided;3H16
Area of tension reinforcement provided; A_s,prov = 603 mm²

Minimum area of reinforcement – exp.9.1N; A_s,min = max(0.26 × f_ctm / f_yk, 0.0013) × b × d = 122 mm²
Maximum area of reinforcement – cl.9.2.1.1(3); A_s,max = 0.04 × b × h = 4140 mm²
PASS – Area of reinforcement provided is greater than area of reinforcement required

Deflection control

Reference reinforcement ratio; ρ_m0 = (f_ck )^0.5 / 1000 = 0.00500
Required tension reinforcement ratio; ρ_m = A_s,req / (b_eff × d) = 0.00168
Required compression reinforcement ratio; ρ’_m = A_s2,req / (b_eff × d) = 0.00000

Structural system factor – Table 7.4N; K_b = 0.4
Basic allowable span to depth ratio ; span_to_depth_basic = K_b × [11 + 1.5 × (f_ck)^0.5 × ρ_m0 / ρ_m + 3.2 × (f_ck)^0.5 × (ρ_m0/ρ_m – 1)^1.5] = 31.160

Reinforcement factor – exp.7.17;K_s = min(A_s,prov / A_s,req × 500 N/mm² / f_yk, 1.5) = 1.262
Flange width factor; F1 = if(b_eff / b > 3, 0.8, 1) = 0.800
Long span supporting brittle partition factor; F2 = 1 = 1.000
Allowable span to depth ratio; span_to_depth_allow = min(span_to_depth_basic × K_s × F1 × F2, 40 × K_b) = 16.000
Actual span to depth ratio; span_to_depth_actual = L_{m1_s2} / d = 6.266

PASS – Actual span to depth ratio is within the allowable limit

Shear Design

Angle of comp. shear strut for maximum shear; θ_max = 45 deg
Strength reduction factor – cl.6.2.3(3);  v₁ = 0.6 × (1 – f_ck / 250) = 0.540
Compression chord coefficient – cl.6.2.3(3); α_cw = 1.00

Minimum area of shear reinforcement – exp.9.5N;   A_sv,min = 0.08 N/mm² × b × (f_ck )^0.5 / f_yk = 184 mm²/m

Design shear force at support ;  V_Ed,max = 63 kN
Min lever arm in shear zone;  z = 379 mm
Maximum design shear resistance – exp.6.9; V_Rd,max = α_cw × b × z × v₁ × f_cwd / (cot(θ_max) + tan(θ_max)) = 392 kN
PASS – Design shear force at support is less than maximum design shear resistance

Design shear force at 399mm from support; V_Ed = 53 kN

Design shear stress; v_Ed = V_Ed / (b × z) = 0.608 N/mm²
Angle of concrete compression strut – cl.6.2.3; θ = min(max(0.5 × Asin(min(2 × v_Ed / (α_cw × f_cwd × v₁),1)), 21.8 deg), 45deg) = 21.8 deg

Area of shear reinforcement required – exp.6.8; A_sv,des = v_Ed × b / (f_yd × cot(θ)) = 129 mm²/m
Area of shear reinforcement required; A_sv,req = max(A_sv,min, A_sv,des) = 184 mm²/m

Shear reinforcement provided; 2 × 8 legs @ 200 c/c
Area of shear reinforcement provided; A_sv,prov = 503 mm²/m
PASS – Area of shear reinforcement provided exceeds minimum required

Maximum longitudinal spacing – exp.9.6N; s_vl,max = 0.75 × d = 299 mm
PASS – Longitudinal spacing of shear reinforcement provided is less than maximum