How to Apply Wind Load on Roofs of Buildings

Wind load is one of the significant actions on roofs. While other loads such as the self-weight of materials, imposed loads, service loads, and snow loads are pointed downwards, wind load on roofs tends to pull the roof upwards. As a result, when wind load is acting on roofs, there is a possibility of the reversal of internal forces in the members of the roofs trusses or rafters from tensile to compressive or vice versa. This is why the application of wind load on roofs is so important.

The method for the application of wind load on roofs is given in EN 1991-1-4:2005 (Eurocode 1 Part 4). The effect of wind on any structure (i.e. the response of the structure), depends on the size, shape, and dynamic properties of the structure. Wind action is represented by a simplified set of pressures or forces whose effects are equivalent to the extreme effects of the turbulent wind. It is important to note that the wind actions calculated using EN 1991-1-4 are characteristic values and are determined from the basic values of wind velocity or velocity pressure. Unless otherwise specified, wind actions are classified as variable fixed actions.

Procedure for the calculation of Wind Load on Roofs

(1) Determine the peak velocity pressure q_p by calculating/obtaining the following values;

• basic wind velocity V_b
• reference height Z_e
• terrain category
• characteristic peak velocity pressure q_p
• turbulence intensity I_v
• mean wind velocity V_m
• orography coefficient c_o(z)
• roughness coefficient c_r(z)

(2) Calculate the wind pressures using the pressure coefficients;

• external pressure coefficient c_pe
• internal pressure coefficient C_pi
• net pressure coefficient c_p,net
• external wind pressure: w_e = q_p c_pe
• internal wind pressure: W_i = q_p C_p

(3) Calculate the wind force

• determine the structural factor: C_sC_d
• wind force F_w calculated from force coefficients
• wind force F_w calculated from pressure coefficients

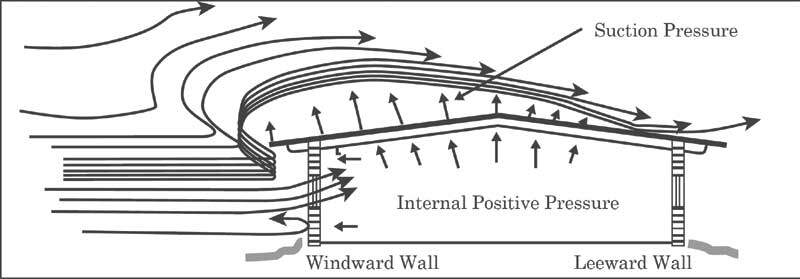
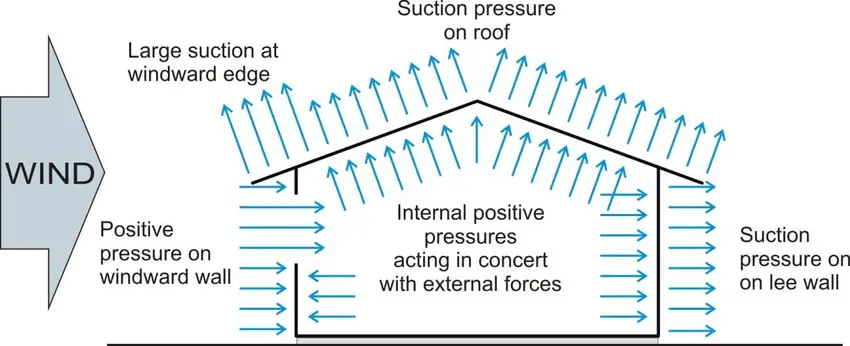
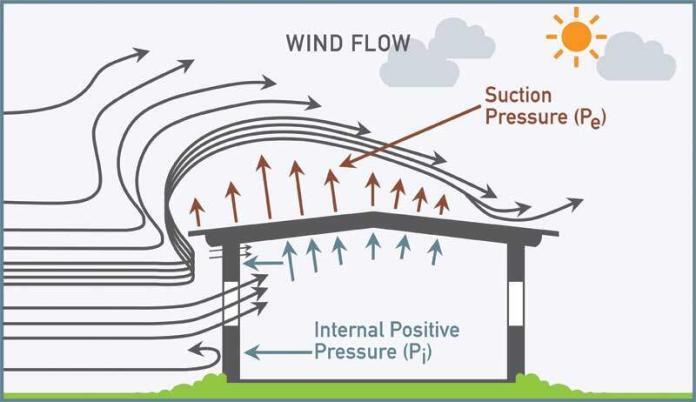
A pioneering wind tunnel experiment (Stanton, 1908) showed that when the roof slope is greater than 70 degrees from horizontal on the windward side, the roof surface can be treated as a vertical surface, with the external pressure coefficient c_pe equal to +0.5 (positive). The positive normal wind pressure reduces as the roof slope lowers. The pressure drops to zero when the roof slope approaches 30 degrees. A negative normal pressure (suction) acts upwardly normal to the slope when the roof slope falls below 30°.

As the slope declines, the suction pressure increases until it reaches its maximum value when the slope is zero (i.e. a flat roof). If the roof slope is 45 degrees, for example, c_pe = (45/100 – 0.2) = +0.25. If the roof slope is 30°, c_pe = (30/60 – 0.5) = 0.0. If the roof slope is 10° c_pe = (10/30 – 1.0) = -0.67 (upwards suction). If the roof slope is 0°, c_pe = (0/30 – 1) = 1.0 (upwards suction).

Based on the same experiment results, c_pe = -1.0 (upwards suction) for all roof slopes on the leeward roof slope. Thus, c_pe = 1.0 (upwards suction) for the windward part of a flat roof and c_pe = -0.5 (upwards suction) for the leeward side.

A building is subjected to internal pressures due to apertures in the walls, in addition to external wind pressures. Therefore, we have to also consider the internal pressure coefficients c_pi. The result of wind blowing into a building through an opening facing the opposite direction as the wind blowing onto the building is the formation of internal pressure within the structure.

Positive internal pressure: When wind blows into an open-sided building or into a workshop through a large open door, the internal pressure seeks to force the roof and side coverings outwards, resulting in positive internal pressure.

Negative internal pressure (suction): This is formed within a building when the wind blows in the opposite direction, tending to pull the roof and side coverings inwards.

The coefficient of internal suction c_pi = ±0.2 in normal permeability shops (covered with corrugated sheets), and ±0.5 in buildings with extensive apertures (in the case of industrial buildings). Internal suction, or pressure away from the interior surfaces, is shown by a negative number, whereas internal pressure is indicated by a positive value.

Worked Example

Calculate the wind action on the walls and roof of a building with the data given below. Consider when the wind is coming perpendicular (0°) to the length of the building, and normal to it (90°).

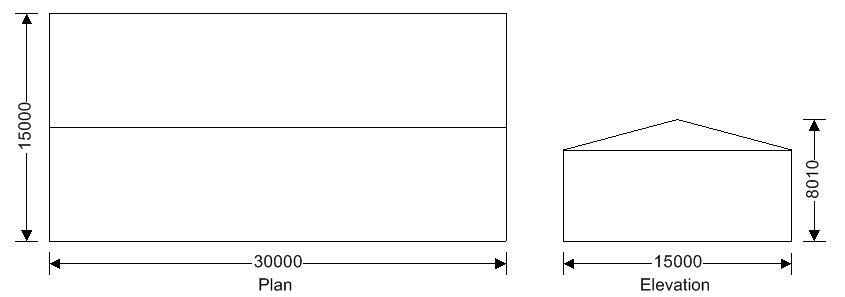
Building data
Type of roof; Duopitch
Length of building;  L = 30000 mm
Width of building;  W = 15000 mm
Height to eaves; H = 6000 mm
Pitch of roof;  α₀ = 15.0°
Total height;  h = 8010 mm

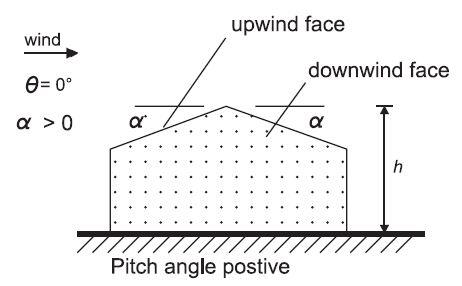
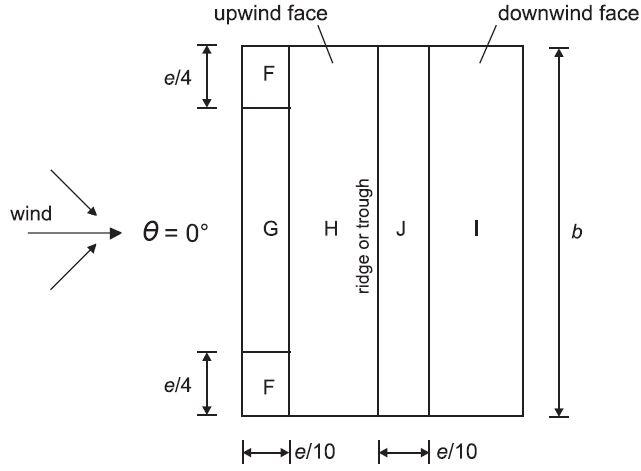
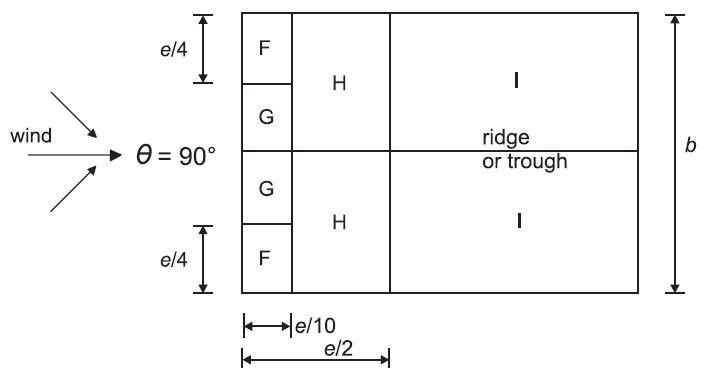
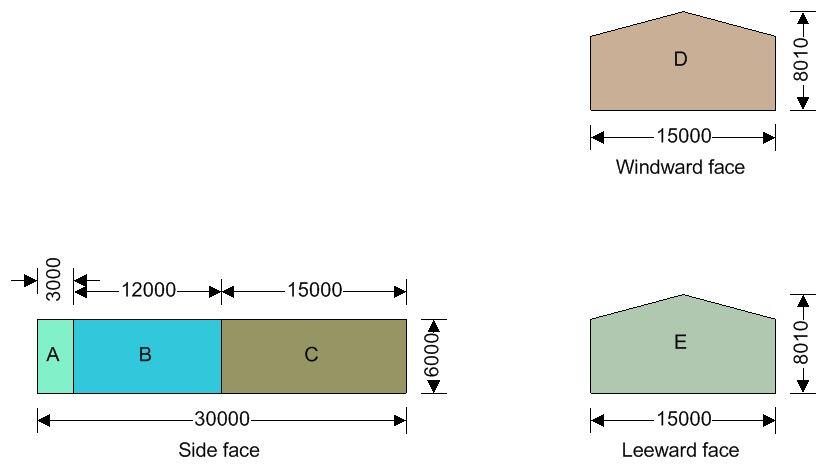
Tekla Tedds will be used for executing the wind load analysis on the building. The key to the pressure coefficients for a building with a duopitch roof is given below (Figure 7.8 EN 1991-1-1:2005). Note that e = B or 2h whichever is smaller, where b is the crosswind dimension.

Location of building; Onitsha, Anambra State, Nigeria
Wind speed velocity; v_b,map = 40.0 m/s
Distance to shore; L_shore = 50.00 km
Altitude above sea level; A_alt = 50.0m

Altitude factor;c_alt = A_alt/1m × (0.001 + 1) = 1.050
Fundamental basic wind velocity; v_b,0 = v_b,map × c_alt = 42.0 m/s
Direction factor; c_dir = 1.00
Season factor; c_season = 1.00
Shape parameter K; K = 0.2
Exponent n; n = 0.5
Air density; ρ = 1.226 kg/m³

Probability factor;  c_prob = [(1 – K × ln(-ln(1-p)))/(1 – K × ln(-ln(0.98)))]ⁿ = 1.00
Basic wind velocity (Exp. 4.1); v_b = c_dir × c_season × v_b,0 × c_prob = 42.0 m/s
Reference mean velocity pressure;  q_b = 0.5 × ρ × v_b² = 1.081 kN/m²

Orography
Orography factor not significant; c_o = 1.0
Terrain category; Country
Displacement height (sheltering effect excluded);   h_dis = 0 mm

The velocity pressure for the windward face of the building with a 0 degree wind is to be considered as 1 part as the height h is less than b (cl.7.2.2). The velocity pressure for the windward face of the building with a 90 degree wind is to be considered as 1 part as the height h is less than b (cl.7.2.2)

Peak velocity pressure  – windward wall – Wind 0 deg and roof

Reference height (at which q is sought); z = 6000 mm
Displacement height (sheltering effects excluded); h_dis = 0 mm
Exposure factor (Figure NA.7); c_e = 2.05
Peak velocity pressure; q_p = c_e × q_b = 2.22 kN/m²

Structural factor
Structural damping;  δ_s = 0.100
Height of element; h_part = 6000 mm
Size factor (Table NA.3);  c_s = 0.884
Dynamic factor (Figure NA.9); c_d = 1.003
Structural factor;  c_sCd = c_s × c_d = 0.887

Peak velocity pressure  – windward wall – Wind 90 deg and roof
Reference height (at which q is sought);  z = 8010 mm
Displacement height (sheltering effects excluded); h_dis = 0 mm
Exposure factor (Figure NA.7);  c_e = 2.23
Peak velocity pressure; q_p = c_e × q_b = 2.41 kN/m²

Structural factor
Structural damping; δ_s = 0.100
Height of element;  h_part = 8010 mm
Size factor (Table NA.3);  c_s = 0.911
Dynamic factor (Figure NA.9); c_d = 1.016
Structural factor; c_sCd = c_s × c_d = 0.925

Structural factor – roof 0 deg

Structural damping; δ_s = 0.100
Height of element; h_part = 8010 mm
Size factor (Table NA.3); c_s = 0.888
Dynamic factor (Figure NA.9); c_d = 1.003
Structural factor; c_sCd = c_s × c_d = 0.891

Peak velocity pressure for internal pressure
Peak velocity pressure – internal (as roof pressure); q_p,i = 2.41 kN/m²

Pressures and forces
Net pressure; p = c_sCd × q_p × c_pe – q_p,i × c_pi
Net force; F_w = p_w × A_ref

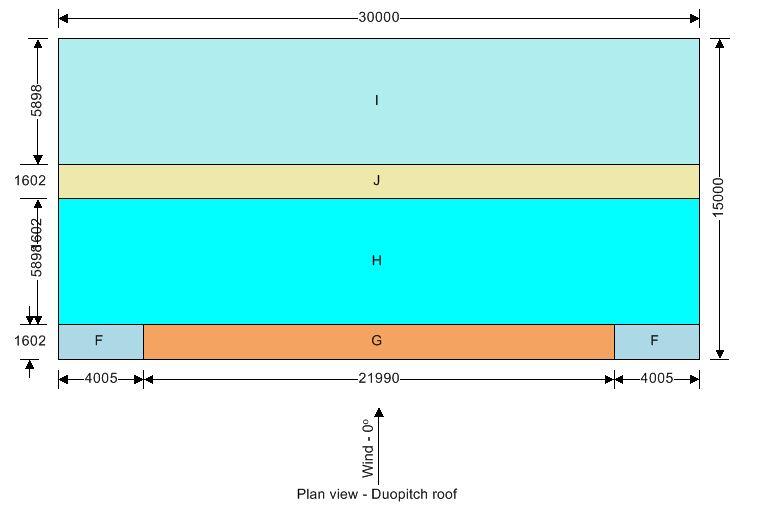
Roof load case 1 – Wind 0, c_pi 0.20, -c_pe

Zone	Ext pressure coefficient cpe	Peak velocity pressure qp, (kN/m2)	Net pressure p (kN/m2)	Area Aref (m2)	Net force Fw (kN)
F (-ve)	-1.10	2.41	-2.84	13.28	-37.78
G (-ve)	-0.80	2.41	-2.20	36.47	-80.23
H (-ve)	-0.40	2.41	-1.34	183.18	-245.64
I (-ve)	-0.50	2.41	-1.56	183.18	-284.97
J (-ve)	-1.30	2.41	-3.27	49.75	-162.87

Total vertical net force; F_w,v = -783.83 kN
Total horizontal net force; F_w,h = 21.79 kN

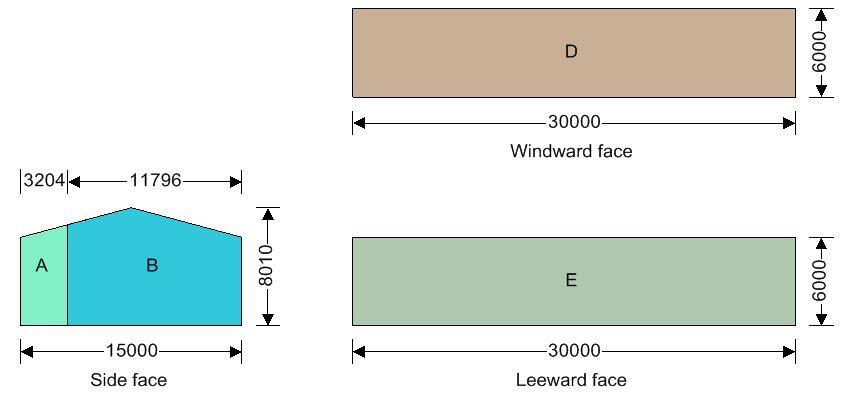
Walls load case 1 – Wind 0, c_pi 0.20, -c_pe

Zone	Ext pressure coefficient cpe	Peak velocity pressure qp, (kN/m2)	Net pressure p (kN/m2)	Area Aref (m2)	Net force Fw (kN)
A	-1.20	2.41	-3.05	20.60	-62.77
B	-0.80	2.41	-2.19	84.47	-185.17
D	0.74	2.22	0.97	180.00	174.37
E	-0.38	2.22	-1.22	180.00	-219.73

Overall loading

Equivalent leeward net force for overall section; F_l = F_w,wE = -219.7 kN
Net windward force for overall section; F_w = F_w,wD = 174.4 kN
Lack of correlation (cl.7.2.2(3) – Note);  f_corr = 0.85; as h/W is 0.534
Overall loading overall section; F_w,D = f_corr × (F_w – F_l + F_w,h) = 353.5 kN

Roof load case 2 – Wind 0, c_pi -0.3, +c_pe

Zone	Ext pressure coefficient cpe	Peak velocity pressure qp, (kN/m2)	Net pressure p (kN/m2)	Area Aref (m2)	Net force Fw (kN)
F (+ve)	0.20	2.41	1.15	13.28	15.31
G (+ve)	0.20	2.41	1.15	36.47	42.03
H (+ve)	0.20	2.41	1.15	183.18	211.11
I (+ve)	-0.50	2.41	-0.35	183.18	-64.23
J (+ve)	-1.30	2.41	-2.07	49.75	-102.91

Total vertical net force; F_w,v = 97.86 kN
Total horizontal net force;  F_w,h = 112.74 kN

Walls load case 2 – Wind 0, c_pi -0.3, +c_pe

Zone	Ext pressure coefficient cpe	Peak velocity pressure qp, (kN/m2)	Net pressure p (kN/m2)	Area Aref (m2)	Net force Fw (kN)
A	-1.20	2.41	-1.84	20.60	-37.94
B	-0.80	2.41	-0.99	84.47	-83.38
D	0.74	2.22	2.17	180.00	391.28
E	-0.38	2.22	-0.02	180.00	-2.83

Overall loading
Equivalent leeward net force for overall section; F_l = F_w,wE = -2.8 kN
Net windward force for overall section; F_w = F_w,wD = 391.3 kN
Lack of correlation (cl.7.2.2(3) – Note); f_corr = 0.85; as h/W is 0.534
Overall loading overall section; F_w,D = f_corr × (F_w – F_l + F_w,h) = 430.8 kN

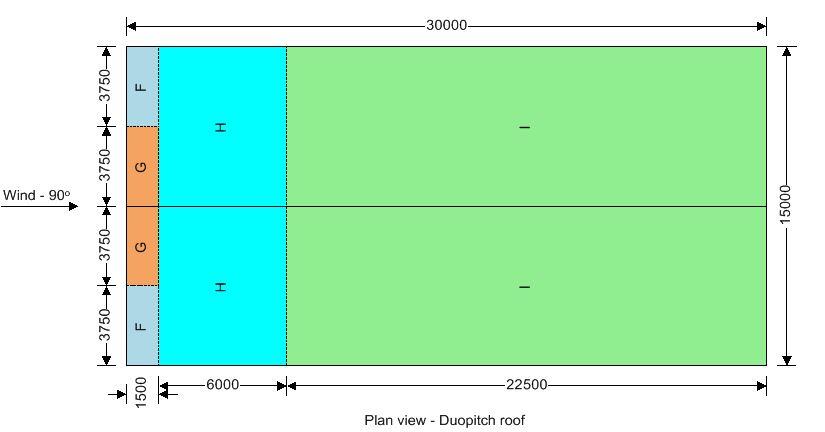
Roof load case 3 – Wind 90, c_pi 0.20, -c_pe

Zone	Ext pressure coefficient cpe	Peak velocity pressure qp, (kN/m2)	Net pressure p (kN/m2)	Area Aref (m2)	Net force Fw (kN)
F (-ve)	-1.60	2.41	-4.05	11.65	-47.17
G (-ve)	-1.50	2.41	-3.83	11.65	-44.58
H (-ve)	-0.60	2.41	-1.82	93.17	-169.59
I (-ve)	-0.40	2.41	-1.37	349.41	-480.12

Total vertical net force; F_w,v = -716.21 kN
Total horizontal net force;  F_w,h = 0.00 kN

Walls load case 3 – Wind 90, c_pi 0.20, -c_pe

Zone	Ext pressure coefficient cpe	Peak velocity pressure qp, (kN/m2)	Net pressure p (kN/m2)	Area Aref (m2)	Net force Fw (kN)
A	-1.20	2.22	-2.94	18.00	-52.99
B	-0.80	2.22	-2.12	72.00	-152.86
C	-0.50	2.22	-1.51	90.00	-135.69
D	0.70	2.41	1.08	105.07	113.92
E	-0.30	2.41	-1.16	105.07	-122.01

Overall loading
Equiv leeward net force for overall section; F_l = F_w,wE = -122.0 kN
Net windward force for overall section; F_w = F_w,wD = 113.9 kN
Lack of correlation (cl.7.2.2(3) – Note); f_corr = 0.85; as h/L is 0.267
Overall loading overall section; F_w,D = f_corr × (F_w – F_l + F_w,h) = 200.5 kN

Roof load case 4 – Wind 90, c_pi -0.3, +c_pe

Zone	Ext pressure coefficient cpe	Peak velocity pressure qp, (kN/m2)	Net pressure p (kN/m2)	Area Aref (m2)	Net force Fw (kN)
F (+ve)	0.20	2.41	1.17	11.65	13.62
G (+ve)	0.20	2.41	1.17	11.65	13.62
H (+ve)	0.20	2.41	1.17	93.17	108.93
I (+ve)	0.20	2.41	1.17	349.41	408.48

Total vertical net force;  F_w,v = 526.08 kN
Total horizontal net force; F_w,h = 0.00 kN

Walls load case 4 – Wind 90, c_pi -0.3, +c_pe

Zone	Ext pressure coefficient cpe	Peak velocity pressure qp, (kN/m2)	Net pressure p (kN/m2)	Area Aref (m2)	Net force Fw (kN)
A	-1.20	2.22	-1.74	18.00	-31.30
B	-0.80	2.22	-0.92	72.00	-66.10
C	-0.50	2.22	-0.30	90.00	-27.24
D	0.70	2.41	2.29	105.07	240.54
E	-0.30	2.41	0.04	105.07	4.60

Overall loading

Equiv leeward net force for overall section; F_l = F_w,wE = 4.6 kN
Net windward force for overall section;  F_w = F_w,wD = 240.5 kN
Lack of correlation (cl.7.2.2(3) – Note);  f_corr = 0.85; as h/L is 0.267
Overall loading overall section; F_w,D = f_corr × (F_w – F_l + F_w,h) = 200.5 kN

References
(1) BS EN 1991-1-4: 2005, Actions on structures. General actions. Wind actions
(2) Stanton, T. E., 1908. Experiments on wind pressure. Minutes of the Proceedings of the Institution of Civil Engineers, 171, 175–200.