Practical Analysis and Design of Steel Roof Trusses

The most widespread alternative for roof construction in Nigeria is the use of trusses, of which timber and steel are the primary choices of materials. An advantage of using trusses for roofs is that ducts and pipes that are required for the operation of the building’s services can be installed through the truss web. However, careful attention must be paid to the design of the truss members and their connection (which may be welded or bolted) since their failure can be catastrophic both in terms of loss of life and economy.

The roof of a church building in Uyo, Akwa Ibom State, Nigeria collapsed on the 10th of December 2016 and left more than 60 worshippers dead, and many injured. This is to show how important, and why engineers must pay careful attention to such design situations. The aim of this article is to show in the clearest manner, how steel truss members can be designed according to EN 1993-1-1-:2005 (Eurocode 3) design code.

A truss is basically a system of triangulated members that are connected and designed to carry load. A truss is inherently stable in shape and resists load by developing primarily axial forces which might be tensile or compressive in nature. The connections in trusses are always assumed to be nominally pinned. When the connection of trusses is stiff, secondary effects such as bending moment and shear force are induced in the truss members.

For a good structural performance of roof trusses, the ratio of span to truss depth should be in the range of 10 to 15. However, it should be noted that the architectural design of the building determines its external geometry and governs the slope given to the top chord of the truss.

For the design of a compression member in a roof truss, several buckling modes need to be considered. In most truss members, only flexural buckling of the compressed members in the plane of the truss structure and out of the plane of the truss structure need to be evaluated. The flexural buckling in Eurocode 3 is achieved by applying a reduction factor to the compression resistance.

Example on the Design of Steel Roof Trusses

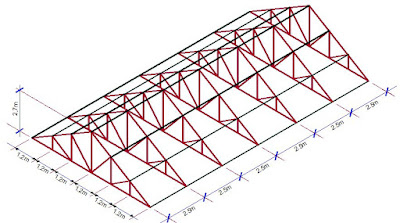
To illustrate this, a simple design example has been presented. The skeletal structure of a roof system (18.0m long and 7.2m wide) is as shown in the Figure below. The truss is made up of Howe Truss configuration spaced at 3m intervals. It is desired to specify the appropriate angle sections that will safely carry the anticipated loading using Eurocode design code (Specified steel grade S 275).

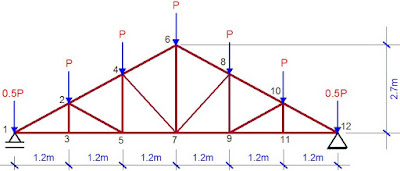
The idealised 2D model of the roof truss typical loading configuration is as shown below;

Load Analysis
Span of roof truss = 7.2m
Spacing of the truss = 3.0m
Nodal spacing of the trusses = 1.2m

Permanent (dead) Loads
Self-weight of long span aluminium roofing sheet (0.55mm gauge thickness) = 0.019 kN/m²
Weight of ceiling (adopt 10mm insulation fibre board) = 0.077 kN/m²
Weight of services = 0.1 kN/m²
Weight of purlin (assume CH 150 x 75 x 18 kg/m) = (18 x 3m)/(1.2 x 3) = 15 kg/m² = 0.147 kN/m²
Self weight of trusses (assume) = 0.2 kN/m²
Total deal load (g_k) = 0.536 kN/m²
Therefore the nodal permanent load (g_k) = 0.536 kN/m² × 1.2m × 3m = 1.9296 kN

Variable (Imposed) Load
Category of roof = Category H – Roof not accessible except for normal maintenance and repairs (Table 6.9 EN 1991-1-1:2001)
Imposed load on roof (q_k) = 0.75 kN/m²
Therefore the nodal variable load (Q_K) = 0.75 kN/m² × 1.2m × 3m = 2.7 kN

Wind Load
Wind velocity pressure (dynamic) is assumed as = q_p(z) = 1.5 kN/m²
When the wind is blowing from right to left, the resultant pressure coefficient on the windward and leeward slopes with positive internal pressure (c_pe) is taken as −0.9
Therefore the external wind pressure normal to the roof is;
q_e = q_pc_pe = −1.5 × 0.9 = 1.35 kN/m²
Vertical component p_ev = q_e cos θ = 1.35 × cos 36.869 = 1.08 kN/m² acting upwards ↑
Therefore the nodal wind load (W_k) = 1.08 kN/m² × 1.2m × 3m = 3.888 kN
To see how wind load is analysed using Eurocode, click HERE

Analysis of the Truss for Internal Forces
N/B: Please note that the internal forces in the members are denoted by F_i-j which is also equal to F _j-i e.g. F _2-3 = F _3-2 ; so kindly distinguish this from other numeric elements

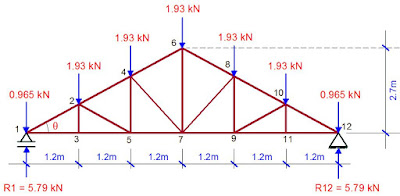
Dead Load

JOINT 1

θ = tan^-1⁡(2.7/3.6) = 36.869
Let ∑F_y = 0
5.79 – 0.956 + F_1-2 (sin θ) = 0
F_1-2 = (-4.834)/sin⁡36.869 = -8.0568 kN (COMPRESSION)

Let ∑F_x = 0
F_1-2 (cos θ) + F_1-3 = 0
F_1-3 = -(-8.0568 ×(cos⁡36.869)) = 6.445 kN (TENSION)

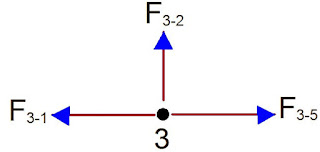
JOINT 3

Let ∑F_y = 0
F_{3 – 2} = 0 (NO FORCE)

Let ∑F_x = 0
F_3–5 – F_3–1 = 0
F_3–1 = F_3–5 = 6.445 kN (TENSION)

JOINT 2

ϕ = tan^-1⁡(0.9/1.2) = 36.869 = θ
Let ∑F_y = 0
-1.93 + F_2-4(sin θ) – F_2–3 – F_2-5(sin θ) – F_2-1(sin θ) = 0
-1.93 + F_2-4(sin 36.869) – 0 – F_2-5(sin 36.869) – [-8.0568(sin 36.869)] = 0
0.6 F_2–4 – 0.6F_2–5 = -2.904 ———- (1)

Let ∑F_x = 0
F_2-4(cos θ) + F_2-5(cos θ) – F_2-1(cos θ) = 0
F_2-4(cos 36.869) + F_2-5(cos 36.869) – [-8.0568(cos36.869)] = 0
0.8 F_2–4 + 0.8 F_2–5 = -6.4455———- (2)

Solving equations (1) and (2) simultaneously;
F_2-4 = – 6.448 kN (COMPRESSION)
F_2-5 = -1.608 kN (COMPRESSION)

JOINT 5

Let ∑F_y = 0
F_5-2(sin ϕ) + F_5–4 = 0
-1.608 (sin 36.869) + F_5–4 = 0
F_5–4 = 0.9646 kN (TENSION)

Let ∑F_x = 0
–F_5–3 – F_5–2 (cos ϕ) + F_5–7 = 0
-6.445– [–1.608 (cos 36.869)] + F_5–7 = 0
F_5–7 = 5.1586 kN (TENSION)

JOINT 4

α = tan^-1(1.8/1.2) = 56.309°
Let ∑F_y = 0
-1.93 – F_4–2 (sin θ) – F_4–5 – F_4–7 (sin α) + F_4–6(sin θ) = 0
-1.93 – [-6.448(sin 36.869)] – 0.9646 – F_4-7 (sin 56.309) + F_4–6 (sin 36.869) = 0
-0.832 F_4–7 + 0.6 F_4–6 = -0.9742 ——– (3)

Let ∑F_x = 0
F_4–7 (cos α) + F_4-6(cos θ) – F_4-2(cos θ) = 0
F_4-7(cos 56.309) + F_4-6(cos 36.869) – (-6.448(cos36.869)) = 0
0.5547 F_4–7 + 0.8 F_4–6 = – 5.1584 ——– (4)

Solving equations (3) and (4) simultaneously;
F_4-7 = – 2.319 kN (COMPRESSION)
F_4-6 = -4.8398 kN (COMPRESSION)

JOINT 6

Let ∑F_x = 0
– F_4-6(cos θ) + F_6-8 (cos θ) = 0
-(-4.8398 cos 36.869) + F_6-8 (cos 36.869) = 0
F_6-8 = (-3.87184)/cos ⁡36.869 = – 4.8398 kN (COMPRESSION)

Let ∑F_y = 0
-1.93 – F_6–4 (sin θ) – F_6–7 – F_6–8 (sin θ) = 0
-1.93 – [-4.8398(sin 36.869)] – F_6–7 – [–4.8398(sin 36.869)] = 0
F_6–7 = 3.8777 kN (TENSION)

SUMMARY OF RESULTS FOR DEAD LOAD (G_K)

BOTTOM CHORD
F_1-3 = 6.445 kN (T)
F_3-5 = 6.445 kN (T)
F_5-7 = 5.158 kN (T)

TOP CHORD
F_1-2 = -8.0568 kN (C)
F_2-4 = -6.448 kN (C)
F_4-6 = -4.839 kN (C)

VERTICALS
F_2-3 = 0 (NO FORCE)
F_4-5 = 0.9646 kN (T)
F_6-7 = 3.877 kN (T)

DIAGONALS
F_2-5 = -1.608 kN (C)
F_4-7 = – 2.319 kN (C)

Similarly, the summary of analysis results for imposed load (Q_k) is given below;

BOTTOM CHORD
F_{1 – 3} = 8.992 kN (T)
F_{3 – 5} = 8.992 kN (T)
F_{5 – 7} = 7.198 kN (T)

TOP CHORD
F_{1 – 2} = -11.241 kN (C)
F_{2 – 4} = – 8.998 kN (C)
F_{4 – 6} = -6.748 kN (C)

VERTICALS
F_{2 – 3} = 0 (NO FORCE)
F_{4 – 5} = 1.346 kN (T)
F_{6 – 7} = 5.391 kN (T)

DIAGONALS
F_{2 – 5} = -2.242 kN (C)
F_{4 – 7} = – 3.238 kN (T)

Summary of Results for Wind Load (W_k)

BOTTOM CHORD
F_{1 – 3} = -12.948 kN (C)
F_{3 – 5} = -12.948 kN (C)
F_{5 – 7} = -10.365 kN (C)

TOP CHORD
F_{1 – 2} = 16.187 kN (T)
F_{2 – 4} = 12.957 kN (T)
F_{4 – 6} = 9.717 kN (T)

VERTICALS
F_{2 – 3} = 0 (NO FORCE)
F_{4 – 5} = – 1.938 kN (C)
F_{6 – 7} = -7.763 kN (C)

DIAGONALS
F_{2 – 5} = 3.228 kN (T)
F_{4 – 7} = 4.662 kN (T)

In all cases, (T) – Tensile force; (C) – Compressive force

Structural Design of Roof Trusses to Eurocode 3

All structural steel employed in the design has the following properties;
f_y (Yield strength) = 275 N/mm²
f_u (ultimate tensile strength = 430 N/mm²)

Design of the bottom chord (considering maximum effects)

LOAD CASE 1: DEAD LOAD + IMPOSED LOAD only
Fu = γ_GjGk + γ_QkQk

Ultimate design force (N_Ed) = 1.35G_k + 1.5Q_k
N_Ed = 1.35(6.445) + 1.5(8.992) = 22.189 kN (TENSILE)

LOAD CASE 2: DEAD LOAD + WIND LOAD acting simultaneously

Partial factor for permanent actions (DK) = γGj = 1.0 (favourable)
Partial factor for leading variable actions (W_k) = γW_k = 1.5

Therefore ultimate design force in the member = Fu = γ_GjGk + γ_WkWk = G_k + 1.5W_k.
N_Ed = 1.0(6.445) – 1.5(12.894) = -12.896 kN (COMPRESSIVE)

Therefore, all bottom chord members should be able to resist an axial tensile load of 22.189 kN and a possible reversal of stresses with a compressive load of 12.896 kN

Length of longest bottom chord member = 1200mm

Consider EQUAL ANGLES UA 50 X 50 X 6
Gross Area = 5.69 cm²
Radius of gyration (axis y-y) r_i = 1.5 cm
Considering one M12 bolt (14mm diameter allowance) – Equivalent tension area = 3.72 cm²
Equivalent tension area for welded connection = 4.88cm²

N_t,Rd is the lesser of;
(A_net × Fy)/γ_M0 and (0.9A_net × fu)/γ_M2
f_u = 430 N/mm²; f_y = 275 N/mm²
N_t,Rd = (3.72 × 10² × 275)/1.0 × 10^-3) = 102.3 kN
Also check; (0.9 × 3.72 × 10² × 430)/1.25 × 10^-3 = 115.17 kN

Therefore;

N_Sd/N_t,Rd = 22.189/102.3 = 0.216 < 1.0 (Section is ok for tension resistance)

Compression and buckling resistance
Thickness of section t = 6 mm. Since t < 16mm, Design yield strength f_y = 275 N/mm² (Table 3.1 EC3)

Section classification
ε = √(235/f_y) = √(235/275) = 0.9244
h/t = 50/6 = 8.33.
Referring to Table 5.2 (sheet 3) of Eurocode 3, Part 1-1, for class 3 classification,
h/t ≤ 15ε and (h + b)/2t ≤ 11.5ε. In our case,
5ε = 15 × 0.92 = 13.8 > h/t (8.3) OK
(h + b)/2t = 8.33 < 10.8 (11.5 × 0.92) OK

Thus, the section satisfies both of the conditions.

Resistance of the member to uniform compression
N_C,Rd = (A × Fy)/γ_M0 = (5.69 × 10² × 275)/1.0 = 156475 N = 156.475 kN
N_Ed/N_C,Rd = 12.896/156.475 = 0.0824 < 1 Therefore section is ok for uniform compression.

Buckling resistance of the member
Since the member is pinned at both ends, critical buckling length is the same for all axis; L_cr = 1200mm
Slenderness ratio λ = L_cr/(r_i × λ₁)
λ₁= 93.9ε = 93.9 × 0.9244 = 86.801
In the planar axis (z-z and y-y)
λ = 1200/(15 × 86.801) = 0.9216

Buckling curve b is appropriate for all angle sections according to Table 6.2 of Eurocode 3
α = 0.34 for buckling curve b
Φ = 0.5 [1 + α(λ – 0.2) + λ²]
Φ = 0.5 [1 + 0.34(0.9216 – 0.2)+ 0.9216²] = 1.0473

X = 1/[Φ + √(Φ² – λ²)]
X = 1/[1.0473 + √(1.047² – 0.9216²)] = 0.6473 < 1

Therefore N_b,Rd = (X × A × f_y)/γ_m1 = (0.6473 × 5.69 × 10²× 275)/1.0 = 101286.2675 N = 101.286 kN
N_Ed/N_b,Rd = 12.869/101.286 = 0.127 < 1 Therefore the section is ok for buckling

Therefore, UA 50 x 50 x 6 is ok to resist all axial loads on the bottom chord of the truss.
Following the method shown above in section 4.0, other members of the truss can be efficiently designed.

Thank you for visiting
TO DOWNLOAD THE FULL DESIGN PAPER IN PRINTABLE PDF FORMAT, CLICK HERE