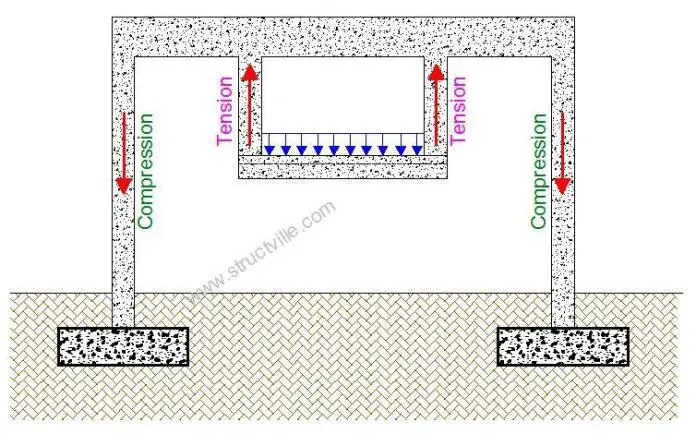
It is more common for reinforced concrete columns in a building to be in compression. This makes sense because, in a conventional load path of a building, gravity loads are transmitted through the columns to the foundation, which exerts an equal and opposite reaction on the column, thereby placing it in compression. For tension columns, the load is probably going somewhere else before being transmitted to the foundation. This is usually deliberate!
The most significant internal force associated with columns is the axial force, even though more often than not, columns are also subjected to bending moment and shear forces. Design equations and charts exist in almost all codes of practice for reinforced concrete columns subjected to compressive axial force, bending moment, and shear. However, when a concrete column is in tension, the approach is usually very cautious. It is advisable to avoid placing concrete columns in tension unless you cannot help it.
Concrete is very good in compression but weak in tension. For instance, for a block of concrete with a 28 days cylinder compressive strength of 25 N/mm2, we will expect the tensile strength to be about 2.6 N/mm2 (See Table 3.1 EN 1992-1-1:2004). In reinforced concrete design, we normally assume the tensile resistance of concrete to be zero unless we are dealing with serviceability issues such as cracking.
If a reinforced concrete column is to be in axial tension, the entire axial stress will be carried by the steel reinforcements, unlike when it is compression. The area of steel required to resist the tensile axial force will be given by;
Ast,req = Nt,Ed/0.87fyk
Where;
Ast,req = Area of steel required
Nt,Ed = Ultimate axial compressive force
fyk = characteristic yield strength of the reinforcement
However, this is not as simple and straightforward as it looks. For a concrete section subjected to a significant axial tensile force, cracking is going to be a major problem. As a result, additional reinforcements will be required to control the cracking, aside from the main reinforcements resisting the axial tension. The additional reinforcements will have to be caged as in the case of a wall reinforcement using smaller diameter bars. The column might have two layers of reinforcements; the inner layer for resisting the tensile force, and the outer layer for controlling the cracking (skin reinforcement).
The maximum bar diameter for the skin reinforcement can be estimated from equation 7.7N of EN 1992-1-1:2004 for members subjected to uniform axial tension;
φs = φ∗s(fct,eff/2.9)hcr/(8(h-d))
where:
φs is the adjusted maximum bar diameter
φ∗s is the maximum bar size given in Table 7.2N of EN 1992-1-1:2004
h is the overall depth of the section
hcr is the depth of the tensile zone immediately prior to cracking, considering the characteristic values of prestress and axial forces under the quasi-permanent combination of actions
d is the effective depth to the centroid of the outer layer of reinforcement
The discussion above has been based on the assumption that the tension column is subjected to pure axial force. However, what happens when there is bending and shear in the section? In that case, the interaction of axial force and bending will have to be considered, and this is expected to have an effect on the size of the tension column and the quantity of the reinforcements.
From the ongoing, it can be seen that structural steel or composite sections are the best for tension columns, provided the connection details are well designed by the structural engineer. The problem of cracking due to low tensile strength is the major challenge of constructing tension columns using reinforced concrete. However, if this can be overcome with the use of additional reinforcements, the problem can be solved at the expense of additional costs.
Furthermore, the reinforcements in tension columns must not be lapped and must be detailed in such a way that the reinforcement hooks and carries the load below it. For reinforcement continuity, mechanical couplers are expected to perform better than lapping.
Practical Applications of Tension Columns
Tension columns are usually floating columns, and transmit the load they are supporting to the member above them. This depends on the structural scheme adopted by the structural engineer. However, when tension columns are to be supported on the ground, uplift forces will have to be properly checked.
An example of the application of tension columns is in the United States Court House in Downtown Los Angeles. The building’s structural system is depicted in the diagram below. All of the columns are set around the perimeter of the structure, but they do not convey the load to the ground; instead, they take the load up. As a result, there is no compressive force applied to the columns.

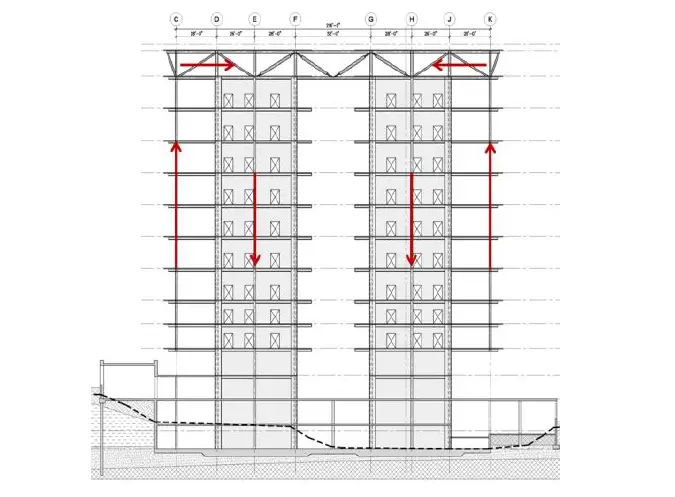
As can be seen above, the slab is not supporting the column’s weight; rather, it is hanging on to it. Therefore, the columns are subjected to axial tension due to the pull from the downward weight of the slab. The load is transferred from the slab to the column, which then passes through the roof truss, which is supported by shear walls. It is however important to note that steel columns were utilised in the construction described above.