Glass is a significant and popular material in contemporary architecture, whether it is used to facilitate the entry of natural light into indoor areas, contribute to exterior aesthetics, or build facades/curtain walls for highrise buildings. It is an inorganic solid with a non-crystalline (amorphous) atomic structure and is produced from a wide variety of constituent materials. However, glass is a relatively new structural material, and its use in this area is a significant development.
Over the past 25 years, there has been a lot of progress in the use of glass as a structural material. This can be seen in the growing number of buildings that use glass for structural elements. One example of a significant implementation from this period is the extension of the Broadfield House Glass Museum in Kingswinford.

The development of glass structures has been driven by advances in glass technology and our understanding of its mechanical and strength properties. The use of structural glass has also led to the development of standards for its design. Today, there are standards covering the design of glass structures, but historically there have been a variety of national regulations that were often contradictory, incomplete, outdated, or not aligned with the European basis of design of EN 1990 (2010).
The European Commission issued a mandate in 2012 for a new generation of Eurocodes, including a new Eurocode for the design of glass structures. This work has resulted in the development of a harmonized European standard, Eurocode 10, which is expected to be published in early 2024.
Types of Glass
Annealed Glass
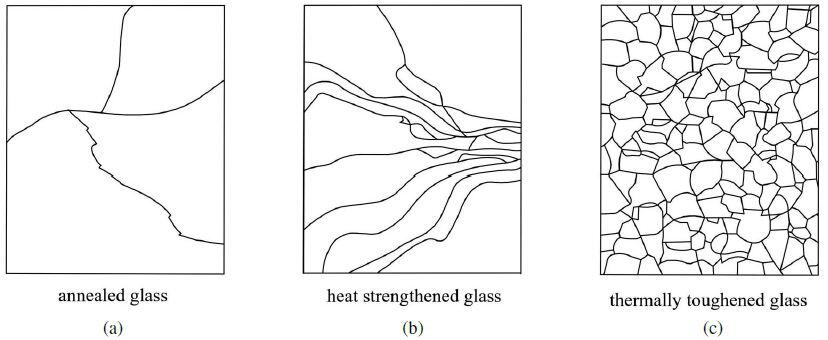
Annealed glass, also known as float glass, is the most common type of glass. It is made by floating molten glass on a bath of molten tin. After the glass is formed, it is annealed, which is a process of slow heating and cooling to remove internal stresses. Annealed glass is relatively weak and susceptible to impact, bending, and thermal stresses. It also breaks into large, sharp shards, which can be dangerous (see Figure 2).

The way annealed glass breaks depends on the flaws in the glass, the stress level, the stressed surface area, and the duration of the load. Flaws in the glass can be caused by the manufacturing process, cutting, grinding, or drilling, or by the environment in which the glass is used (e.g., humidity can promote crack growth).
Heat Strengthened Glass
Heat-strengthened glass is made by heating annealed glass to a temperature slightly above its annealing point and then cooling it quickly. This causes the surface of the glass to cool and solidify first, while the interior of the glass remains hotter. As the interior cools, it tries to shrink, but the surface is preventing it from doing so. This creates a compressive stress on the surface of the glass and a tensile stress in the interior.
This heat treatment makes heat-strengthened glass stronger than annealed glass and more resistant to fracture. When heat-strengthened glass does break, it breaks into smaller pieces than annealed glass, which reduces the risk of injury.
The surface compressive stress of heat-strengthened glass must be greater than 24 MPa but less than 52 MPa. This is to ensure that the glass is strong enough to resist breakage, but not so strong that it is susceptible to spontaneous fracture.
Tempered Glass
Tempered glass, also known as fully tempered or thermally toughened glass, is made in the same way as heat-strengthened glass, but it is cooled more quickly. This causes the surface of the glass to be in more compression and the interior to be in more tension. The surface compressive stress of tempered glass must be greater than 69 MPa.
When tempered glass breaks, it shatters into small, roughly cubic pieces. This is because the tension in the interior of the glass is so great that it causes the glass to break into very small pieces (see Figure 3).

Tempered glass is susceptible to spontaneous breakage due to nickel sulfide (NiS) inclusions. NiS inclusions are small particles of nickel sulfide that can get trapped in the glass during manufacturing. If these inclusions are heated to a certain temperature, they can transform into a larger and more stable form of nickel sulfide. This transformation can cause the glass to break spontaneously.
To reduce the risk of spontaneous breakage, tempered glass should be inspected for NiS inclusions before it is installed. Tempered glass should also be treated carefully during handling and installation to avoid damaging the surface, which could lead to cracks and subsequent breakage.
Mechanical and Strength Properties of Glass
Glass is a brittle material, which means that it is more likely to break suddenly and without warning when compared with other common structural materials. This is because glass contains tiny cracks, which can concentrate stress and cause the glass to fail.
Glass is weak in tension because it is a brittle material. Brittle materials have a strong atomic structure, but they are also very susceptible to cracks. When glass is loaded in tension, it can’t deform like other structural materials, such as steel or concrete. Instead, it fails suddenly at its ultimate tensile strength as shown in Figure 4. This means that there is no warning before glass breaks, which is why it is important to design carefully when using glass as a structural material.
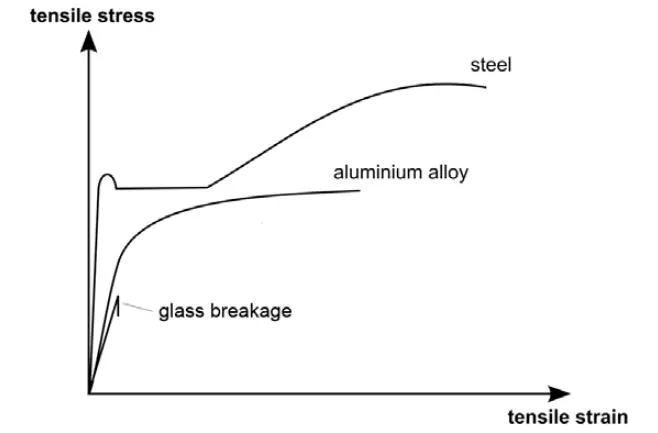
Despite its brittle nature, glass has a theoretical strength of 25-30 GPa, which is very high. However, in real-world applications, the strength of glass is much lower. This is because even small cracks can significantly reduce the strength of glass. The Griffith Theory of Fracture explains why glass is so susceptible to failure. This theory states that the strength of a brittle material is limited by the presence of cracks. The larger the crack, the lower the strength of the material.
To use glass as a structural material, it is important to design structures that minimize the risk of crack formation and propagation. This can be done by using thick glass, avoiding sharp corners, and using appropriate supports.
The typical physical properties of glass are shown in Table 1;
| Property | Symbol | Value |
| Modulus of Elasticity | E | 70,000 N/mm2 |
| Shear modulus | G | 𝐸 [2(1 + 𝜐)] |
| Poisson’s ratio | 𝜐 | 0.22 |
| Coefficient of thermal expansion | 𝛼 | 9 × 10-6 /°C |
| Density | 𝜌 | 2,650 kg/m3 |
Glass is a strong material with a Young’s modulus of 70,000 MPa, which is comparable to aluminium. Its key strength is its bending strength, which is 45 MPa for annealed float glass according to EN 572-1. This value can be increased using thermal or chemical modification processes. Thermal treatment can produce thermally toughened safety glass with a strength of 120 MPa or heat-strengthened glass with a strength of 70 MPa. Chemical treatment can produce glass with a strength of 150 MPa.
As discussed earlier, the fracture pattern of a glass depends on how it has been treated. Annealed float glass breaks into large, sharp shards, while thermally toughened safety glass breaks into a fine mesh of small pieces. Heat-strengthened glass falls somewhere in between. Laminated glass, which is made up of two or more glass panes bonded together with adhesive layers, is the safest type of glass for use in structures because it does not shatter into sharp pieces when it breaks.
Structural Design of Glass Elements
Ultimate limit state
According to the current European standards, the basic method for verification of structural glass is the limit state method. This design concept is also included in the EN 16612 standard for lateral load resistance of linearly supported glazing used as infill panels. The design methodology presented here shall be in accordance with EN 16612 standard, pending the final release of Eurocode 10.
It is subjected to examination for two main conditions:
– determination of the maximum bending stress 𝜎max calculated for the most unfavourable load combinations, which cannot exceed the design value of bending strength fgd:
𝜎max ≤ fgd
– determination of the maximum deflection 𝑤max for the most unfavourable load combinations, which cannot exceed the design value of deflection wd:
𝑤max ≤ wd
The EN 16612 standard requires that the maximum bending stress in the ultimate limit state (ULS) be examined. This is done by calculating the design value of bending strength, fgd. The EN 16612 standard provides methods for calculating fgd for annealed glass and prestressed glass.
fgd = (ke × ksp × kmod × fgk)/γM,A
where:
fgk is the characteristic value of bending strength for annealed glass (45 MPa)
γM,A is the material partial factor for annealed glass (1.8)
ke is the factor for edge strength (typically 1.0)
ksp is the factor for the glass surface profile (typically 1.0)
kmod is the factor for the load duration (typically 1.0)
The design value of bending strength for prestressed glass is obtained from the following formula:
fgd = (ksp × kmod × fgk)/γM,A + kv(fbk – fgk)/γM,v
where;
𝑓𝑔𝑑 – design value of the bending strength,
𝑓𝑏𝑘 – characteristic value of the bending for prestressed glass (70 MPa for heat-strengthened glass and 120 MPa for tempered glass).
𝛾𝑀𝑉 – material partial factor for prestressed glass 𝛾𝑀𝑉 = 1.2,
𝑘𝑉 – factor for strengthening of prestressed glass, for float glass 𝑘𝑉 = 1.0.
In the design formula for bending strength (formula 4.3), the edge strength factor (ke) is used to account for the location of the stresses. The value of ke depends on the type of glass and the quality of the edges. If the glass is supported on all four edges, ke is equal to 1.0. However, if the glass is supported on only two edges, ke may be less than 1.0.
Another important factor in determining the design value of bending strength is the load duration factor (kmod). This factor can be calculated using the following formula;
kmod = 0.663t(-0.0625)
where t is the load duration in hours. The value of kmod ranges from 0.29 to 1.0. Table 4 shows the basic values of kmod for different load durations. The load duration factor is important because glass is a viscoelastic material, which means that its strength decreases over time under sustained load. The kmod factor accounts for this decrease in strength.
| Action | Load duration | Value of kmod |
| Wind gust | 5s (or less) | 1.0 |
| Wind storm load | 10 min | 0.74 |
| Maintenance loads | 30 min | 0.69 |
| Snow load – external canopies and roofs of unheated buildings | 3 weeks | 0.45 |
| Snow load – roofs of heated buildings | 5 days | 0.49 |
| Dead loads, self-weight, altitude load on insulating glass units | Permanent (50 years) | 0.29 |

Solved Examples
(1) Calculate the bending strength of annealed glass for the following load conditions;
(a) Permanent (15 years)
(b) Snow load (roof of heated buildings)
(c) Wind gust load
(a) For permanent load
Load duration = 15 years = 131490 hours; kmod = 0.663 × 131490(-0.0625) = 0.317
fgd = (ke × ksp × kmod × fgk)/γM,A = (1.0 × 1.0 × 0.317 × 45)/1.8 = 7.925 MPa
(b) For snow load
Load duration = 5 days = 120 hours; kmod = 0.663 × 120(-0.0625) = 0.49
fgd = (ke × ksp × kmod × fgk)/γM,A = (1.0 × 1.0 × 0.49 × 45)/1.8 = 12.25 MPa
(c) For wind gust load
Load duration = 5 seconds = 0.00138889 hours; kmod = 0.663 × 0.00138889(-0.0625) = 1.0
fgd = (ke × ksp × kmod × fgk)/γM,A = (1.0 × 1.0 × 0.49 × 45)/1.8 = 25 MPa
(2) Calculate the bending strength of tempered glass for the following load conditions;
(a) Permanent (15 years)
(b) Snow load (roof of heated buildings)
(c) Wind gust load
(a) For permanent load
Load duration = 15 years = 131490 hours; kmod = 0.663 × 131490(-0.0625) = 0.317
fgd = (ksp × kmod × fgk)/γM,A + kv(fbk – fgk)/γM,v = (1.0 × 0.317 × 45)/1.8 + 1.0(120 – 45)/1.2 = 70.5 MPa
(b) For snow load
Load duration = 5 days = 120 hours; kmod = 0.663 × 120(-0.0625) = 0.49
fgd = (ksp × kmod × fgk)/γM,A + kv(fbk – fgk)/γM,v = (1.0 × 0.49 × 45)/1.8 + 1.0(120 – 45)/1.2 = 74.75 MPa
(c) For wind gust load
Load duration = 5 seconds = 0.00138889 hours; kmod = 0.663 × 0.00138889(-0.0625) = 1.0
fgd = (ksp × kmod × fgk)/γM,A + kv(fbk – fgk)/γM,v = (1.0 × 1.0 × 45)/1.8 + 1.0(120 – 45)/1.2 = 87.5 MPa
The lowest design value of bending strength occurs for permanent loads and annealed glass. In this case, the design value is only 18% of the characteristic value of bending strength for annealed glass. The design value is higher for thermally strengthened glass (41%) and thermally toughened safety glass (70%).
However, it is important to note that glass elements are usually subjected to a combination of loads. The standard recommends that the kmod factor be taken at the highest possible value, i.e., for the shortest duration load, when considering combinations of loads. However, all relevant load combinations must be considered. The kmod factor can also be determined as a weighted average.

Serviceability Limit State
The deflection of a glass pane in a structural system should not be so large that it compromises the structural integrity or serviceability of the system. The deflection of a glass pane can be calculated using the finite element method, which can account for large deflections if necessary.
The limit value for the deformation of glass products can vary depending on the type of glass component used. This is because glass is a more sensitive material than other building materials, and even small deformations can be noticeable and uncomfortable for users. Additionally, glass structures can be designed to withstand specific loads and deflections, and exceeding these limits can compromise the structural integrity of the structure.
In other words, the amount of deformation that is allowed for a glass product will depend on a number of factors, including the type of glass, the intended use of the product, and the aesthetic and structural requirements. For example, a glass window will have different deflection limits than a glass staircase.
The serviceability limit state (SLS) in EN 16612 defines different deformation classes for different levels of criticality.
1. SLS as deflections or displacements of pure aesthetical relevance,
2. SLS as deflections or displacements affecting integrity, functionality or durability of the glass component in the unfractured state,
3. SLS as deflection or displacements or effect thereof affecting safety.
The first class 1-SLS is not considered under this standard. For the second class 2-SLS, a typical deflection limit for glass components was defined, which are presented below.
Deflection limit of glass structures
Continuously supported along all edges = L/50 (where L is the length of the short edge)
Continuously supported along 2 or 3 edges = L/100 (where L is the length of the unsupported edge)
Locally clamped at 2 or 3 edges (centre) = L/50 (where L is the length of the short edge)
Locally clamped at 2 or 3 edges (free edge) = L/100 (where L is the length of the unsupported edge)
In HongKong, the deflection of rectangular glass plates can be calculated using the equation below;
Four sides simply supported;
𝛿 = 𝑡∙er0+r1𝑥+r2𝑥2
Where 𝑥 = In [In (p(ab)2/Et4)]
For two sides simply supported;
𝛿 = 5/32 (pa4/Et3)
where;
𝛿 = Centre deflection (mm)
a = Length of shorter side of glass pane (mm)
or loaded span in two-side simply supported case (mm).
𝑏 = Length of longer side of glass pane (mm)
𝑡 = Minimum glass pane thickness (mm)
𝑝 = Design pressure on individual glass pane (kPa)
𝐸 = Modulus of elasticity of glass pane (kPa)
r0 = 0.553 − 3.83(b/a) + 1.11(b/a)2 − 0.0969(b/a)3
𝑟1 = −2.29 + 5.83(b/a) − 2.17(b/a)2 + 0.2067(b/a)3
𝑟2 = 1.485 − 1.908(b/a) + 0.815(b/a)2 − 0.0822(b/a)3
The deflection limit (𝛿limit) of the glass pane should be taken as follows:
- Four-side simply supported: 𝛿limit = 1/60 of the short span
- Three-side simply supported: 𝛿limit = min. [b/60 , a/30]
- Two-side simply supported: 𝛿limit =1/60 of the loaded span
- Cantilever: 𝛿limit = 1/30 of the span
- Point supported: 𝛿limit = 1/60 of the longer span between supports
Conclusion
Glass structures are a prominent feature of modern architecture, serving both aesthetic and functional purposes. They showcase the versatility and transparency of glass, which is used to create entire facades, roofs, and even floors in buildings. Glass structures allow natural light to permeate interior spaces, creating a unique design aesthetic.
However, it is important to design glass structures carefully to ensure that they are safe and durable. This is because glass is a brittle material that can break if it is not properly supported. Glass structures need to be designed to withstand all of the loads that they will be subjected to during their lifetime. This includes both the permanent loads (such as the weight of the glass itself) and the variable loads (such as wind and snow loads.
The design of glass structures requires careful consideration of load-bearing capabilities, thermal expansion, and resistance to various stresses, such as wind and seismic forces. Engineers and architects use advanced materials and engineering techniques, such as laminated or tempered glass, to ensure the strength and safety of these structures.










