Flownets: Two-Dimensional Flow of Water Through Soils

Laplace’s equation is used to describe the movement of water through soils. By comparison, the flow of water through soils is analogous to the steady-state heat flow and steady-state current flow in homogeneous conductors. Flownets can be used to calculate the flow of water through soils based on the Laplace’s equation. The common form of Laplace’s equation for the flow of water through two-dimensional soils is:

k_x(∂²H/∂x²) + k_z(∂²H/∂z²) = 0 ——– (1)

where H is the total head and k_x and k_z are the hydraulic conductivities in the X and Z directions. The condition that the changes in hydraulic gradient in one direction are balanced by changes in the other directions is expressed by Laplace’s equation.

The assumptions in Laplace’s equation are:

• Darcy’s law is valid.
• Irrotational flow (vorticity) is negligible. This assumption leads to the following two-dimensional relationship in velocity gradients.

∂v_z / ∂Z = ∂v_x / ∂X

where v_z and v_x are the velocities in the Z and X directions, respectively. This relationship is satisfied for a uniform flow field and not a general flow field. Therefore, we will assume all flows in this chapter are uniform, i.e., v_z = v_x = constant.
• There is inviscid flow. This assumption means that the shear stresses are neglected.
• The soil is homogeneous and saturated.
• The soil and water are incompressible (no volume change occurs).

Laplace’s equation is also called the potential flow equation because the velocity head is neglected. If the soil is an isotropic material, then k_x = k_z and Laplace’s equation becomes;

(∂²H/∂x²) + (∂²H/∂z²) = 0 ——– (2)

Any differential equation requires knowledge of the boundary conditions in order to be solved. Since the boundary conditions of the majority of “real” structures are complex, an analytical or closed-form solution cannot be obtained for these structures. Using numerical techniques such as finite difference, finite element, and boundary element, it is possible to obtain approximate solutions.

We can also attempt to replicate the flow through the actual structure using physical models. There are two major techniques for solving Laplace’s equation. The first is an approximation known as flownet sketching, and the second is the finite difference method. In this article, we are going to focus on flownet sketching.

Flownet Sketching

The flownet sketching technique is straightforward and adaptable, and it represents the flow regime. It is the preferred method of analysing flow through soils for geotechnical engineers. Before delving into these solution techniques, however, we will establish a few key conditions necessary to comprehend two-dimensional flow.

The solution of Equation (1) is solely dependent on the total head values within the flow field in the XZ plane. Let us introduce a velocity potential (ξ) that describes the variation of total head in a soil mass as follows:

ξ = kH ——– (3)

where k is a generic hydraulic conductivity. The velocities of flow in the X and Z directions are;

v_x = k_x(∂H/∂x) = ∂ξ/∂x ——– (4a)
v_z = k_z(∂H/∂z) = ∂ξ/∂z ——– (4b)

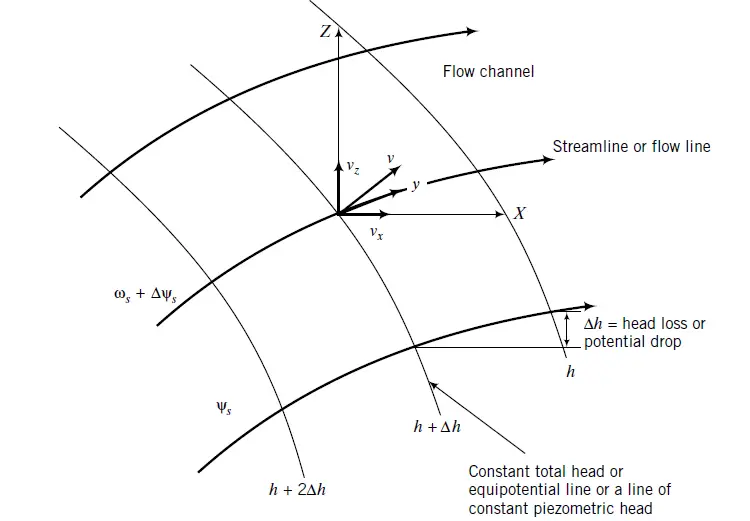
The inference from Equations (4a) and (4b) is that the velocity of flow (v) is normal to lines of constant total head, as illustrated in Figure 1 The direction of v is in the direction of decreasing total head. The head difference between two equipotential lines is called a potential drop or head loss.

If we draw lines that are tangent to the flow velocity at each point in the flow field in the XZ plane, we will obtain a series of lines that are normal to the equipotential lines. These lines are known as streamlines or flow lines (Figure 1). A flow line represents the expected path of a particle of water in a steady-state flow. ψ_s is a stream function that represents a streamline family (x, z). According to the stream function, the components of velocity in the X and Z directions are as follows:

v_x = ∂ψ_s / ∂z ——– (5a)
v_z = ∂ψ_s / ∂x ——– (5b)

Since flow lines are normal to equipotential lines, there can be no flow across flow lines. The rate of flow between any two flow lines is constant. The area between two flow lines is called a flow channel (Figure 1). Therefore, the rate of flow is constant in a flow channel.

Criteria for Sketching Flownets

A flownet is a graphical representation of a flow field that satisfies Laplace’s equation and comprises a family of flow lines and equipotential lines. A flownet must meet the following criteria (Budhu, 2011):

1. The boundary conditions must be satisfied.
2. Flow lines must intersect equipotential lines at right angles.
3. The area between flow lines and equipotential lines must be curvilinear squares. A curvilinear square has the property that an inscribed circle can be drawn to touch each side of the square and continuous bisection results, in the limit, in a point.
4. The quantity of flow through each flow channel is constant.
5. The head loss between each consecutive equipotential line is constant.
6. A flow line cannot intersect another flow line.
7. An equipotential line cannot intersect another equipotential line.

An infinite number of flow lines and equipotential lines can be drawn to satisfy Laplace’s equation. However, only a few are required to obtain an accurate solution. The procedure for constructing a flownet is described next.

Flownet for Isotropic Soils

According to Budhu (2011), the procedure for constructing the flownet of isotropic soils are as follows;

1. Draw the structure and soil mass to a suitable scale.
2. Identify impermeable and permeable boundaries. The soil–impermeable boundary interfaces are flow lines because water can flow along these interfaces. The soil–permeable boundary interfaces are equipotential lines because the total head is constant along these interfaces.
3. Sketch a series of flow lines (four or five) and then sketch an appropriate number of equipotential lines such that the area between a pair of flow lines and a pair of equipotential lines (cell) is approximately a curvilinear square. You would have to adjust the flow lines and equipotential lines to make curvilinear squares. You should check that the average width and the average length of a cell are approximately equal by drawing an inscribed circle. You should also sketch the entire flownet before making adjustments.

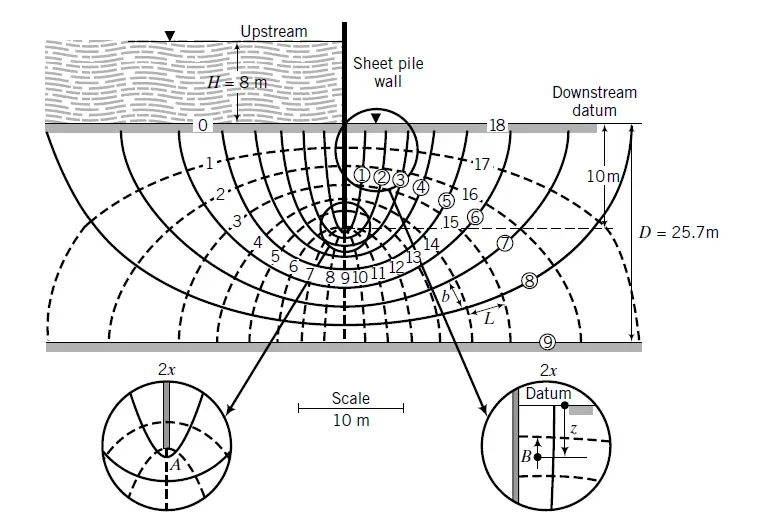
The flownet in confined areas between parallel boundaries typically consists of elliptical and symmetrical flow lines and equipotential lines (Figure 2). Avoid abrupt changes between straight and curved flow and equipotential lines. Transitions should be smooth and gradual. For certain problems, portions of the flownet are enlarged, are not curvilinear squares, and do not satisfy Laplace’s equation.

For instance, the portion of the flownet beneath the base of the sheet pile in Figure 2 is not composed of curvilinear squares. Check these sections to ensure that repeated bisection results in a point for a precise flownet.

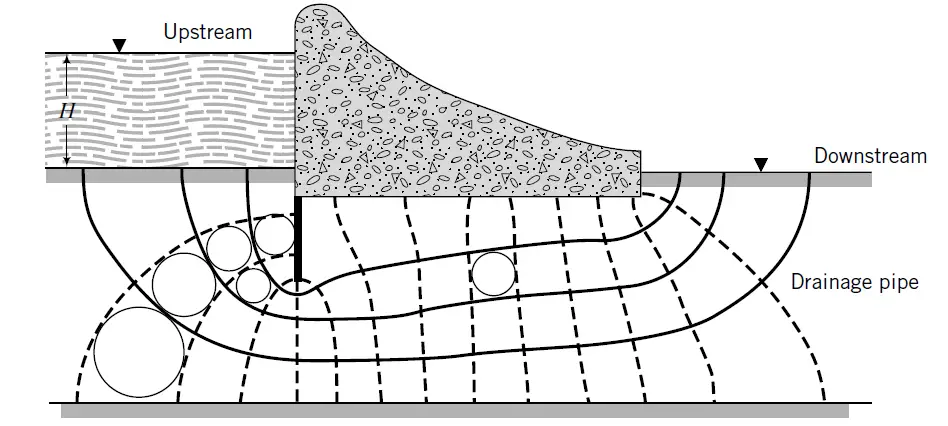
Another example of flownet are shown in Figures 3. Figure 2 shows a flownet for a sheet pile wall, and Figure 3 shows a flownet beneath a dam. In the case of the retaining wall, the vertical drainage blanket of coarse-grained soil is used to transport excess porewater pressure from the backfill to prevent the imposition of a hydrostatic force on the wall. The interface boundary, is neither an equipotential line or a flow line. The total head along the boundary is equal to the elevation head.

Flow Rate

Let the total head loss across the flow domain be ΔH, that is, the difference between upstream and downstream water level elevation. Then the head loss (Δh) between each consecutive pair of equipotential lines is;

Δh = ΔH/N_d ——– (6)

where N_d is the number of equipotential drops, that is, the number of equipotential lines minus one. In Figure 1, ΔH = H = 8 m and N_d = 18. From Darcy’s law, the flow through each flow channel for an isotropic soil is;

q = Aki = (b × 1)k(Δh/L) = kΔh(b/L) = k(ΔH/N_d)(b/L) ——– (7a)

where b and L are defined as shown in Figure 14.3. By construction, b/L = 1, and therefore the total flow is;

q = kΔH(N_f/N_d) ——– (7b)

where N_f is the number of flow channels (number of flow lines minus one). In Figure 1, N_f = 9. The ratio N_f /N_d is called the shape factor. Finer discretization of the flownet by drawing more flow lines and equipotential lines does not significantly change the shape factor. Both N_f and N_d can be fractional. In the case of anisotropic soils, the quantity of flow is;

q = ΔH(N_f/N_d)√(k_xk_z) ——– (8)

Summarily, Flow nets are typically designed for homogeneous, isotropic porous media undergoing saturated flow to known boundaries. There are extensions to the basic method that make it possible to solve the following cases:

• inhomogeneous aquifer: matching conditions at property boundaries
• anisotropic aquifer: drawing the flownet in a transformed domain and scaling the results differently in the principal hydraulic conductivity directions before returning the solution
• one boundary is a seepage face: iteratively solving for both the boundary condition and the solution throughout the domain

The method is typically applied to these types of groundwater flow problems, but it can be applied to any problem described by the Laplace equation, such as the flow of electric current through the earth.

References
Budhu M. (2011): Soil Mechanics and Foundations (3rd Edition). John Wiley & Sons, Inc.