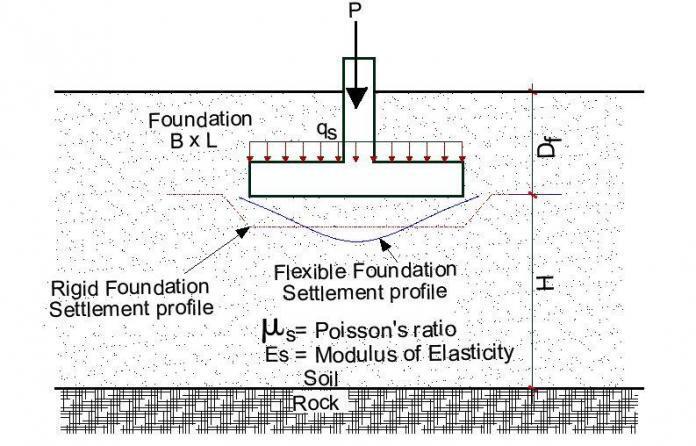
Shallow foundations on natural soils will undergo settlement when loaded. Foundation settlement is mainly made up of elastic (or immediate) settlement, Se, consolidation settlement, Sc. Immediate settlement takes place as the load is applied, or within a period of about 7 days. It is used for all fine-grained soils including silts and clays with a degree of saturation less than or approximately less than 90%, and for all coarse-grained soils with a large coefficient of permeability, say above 10-3 m/s. This article presents a solved example of the elastic settlement of shallow foundations.
It is important to point out that, theoretically at least, a foundation could be considered fully flexible or fully rigid. A uniformly loaded, perfectly flexible foundation resting on an elastic material such as saturated clay will have a sagging profile, as shown in the figure above, because of elastic settlement. However, if the foundation is rigid and is resting on an elastic material such as clay, it will undergo uniform settlement and the contact pressure will be redistributed. The settlement at the centre of a rigid foundation can be estimated as, Se(rigid) ≈ 0.93Se(flexible).
To assess the immediate settlement of a shallow foundation, it is imperative to obtain reliable values of elastic parameters of the soil. Values from the laboratory can contain errors of about 50%, and in-situ tests are often more preferred, with close attention being paid to the anisotropic behaviour of soils.
A range of values for the elastic properties of soils can be seen in Table 1;
| Type of Soil | Modulus of Elasticity Es (MN/m2) | Poisson’s Ratio |
| Loose sand | 10 – 25 | 0.20 – 0.40 |
| Medium dense sand | 15 – 30 | 0.25 – 0.40 |
| Dense sand | 35 – 55 | 0.30 – 0.45 |
| Silty sand | 10 – 20 | 0.20 – 0.40 |
| Sand and gravel | 70 – 170 | 0.15 – 0.35 |
| Soft clay | 4 – 20 | |
| Medium clay | 20 – 40 | 0.20 – 0.50 |
| Stiff clay | 40 – 100 |
It is also necessary to obtain a reliable stress profile from the applied load. We normally have the problem of computing both correct numerical values and the effective depth H of the influence zone. Theory of elasticity equations are used for the stress computation, with the influence depth (H) below the loaded area taken as H = 0, to H = ∞.
However, note that the stratum depth actually causing settlement is not at H/B = ∞, but is at any of the following;
(a) Depth (z) = 5B; where B is the least total lateral dimension of the footing
(b) Depth to where a hard stratum is encountered. Take hard as that stratum where the modulus of elasticity is ten times the modulus of elasticity of the upper layer.
The equation for computing the elastic settlement of a shallow footing is given below;
Where;
qo = net applied pressure on the foundation
μs = Poisson’s ratio of soil
ES = Average modulus of elasticity of the soil under the foundation from z = 0 to about z = 4B or 5B
Due to the non-homogeneous nature of soil deposits, the magnitude of Es may vary with depth. For that reason, Bowles (1987) recommended using a weighted average value of Es as given in equation (2) below;
Where;
ES(i) = Soil modulus of elasticity within a depth ∆z
z ̅ = H or 5B, whichever is smaller
B’ = B/2 for the centre of the foundation, B for the corner of the foundation
IS = Shape factor according to Steinbrenner (1934)
Where;
If = Depth factor which depends on (Df/B, μs, L/B)
Charts for computing If are available in standard geotechnical engineering textbooks.
α = factor that depends on the location on the foundation where settlement is being calculated
For the calculation of settlement at the centre of the foundation;
α = 4; m’= L/B; n’ = H/0.5B
For the calculation of settlement at the corner of the foundation;
α = 1; m’= L/B; n’ = H/B
Worked Example
For the example given below, compute the settlement at the centre of the footing, assuming that a net pressure of 145 kN/m2 is exerted by the foundation.
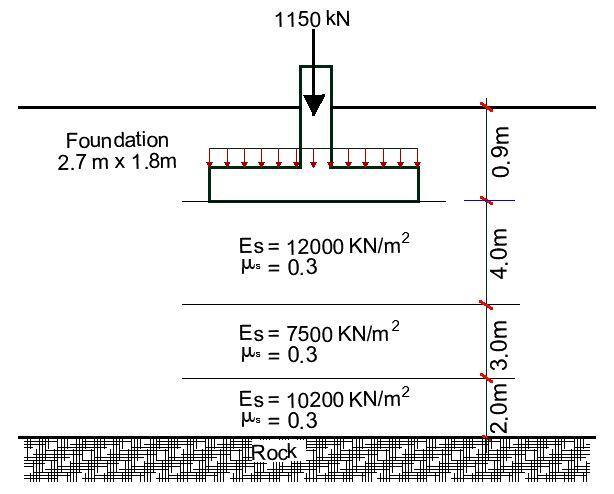
Given that B = 1.8m, L = 2.7m; z ̅ = (5 × 1.8) = 9.0 m = H (9.0 m)
Es = [12000(5) + 7500(3) + 10200(1.2)] / 9 = 10526.667 KN/m2
At the centre of the foundation;
α = 4; m’= L/B =2.7/1.8 =1.5 ; n’ = H/0.5B=9/(0.5(1.8)) = 10
A0 = 1.5 In ((1+ (1.52 + 1)0.5) × (1.52 + 102)) / 1.5 (1 + (1.52+ 102 + 1)0.5)
= 1.5 In(2.803 × 10.112) / (1.5 × 11.161) = 0.7896
A1 = In ((1.5 + (1.52 + 1)) × (1 + 102)) / (1.5 + (1.52 + 102 + 1)0.5)
= In[(3.3027 × 10.049) / (1.5 + 10.161)] = 1.0459
A2 = 1.5 / [10 (1.52 + 102 + 1)0.5] = 1.5 / (10 × 10.161) = 0.0147
F1 = 1/π (A0 + A1 ) = 1/π (0.7896 + 1.0459) = 0.5842
F2 = (n’/2π) tan-1A2 = 10/2π tan-1(0.0147) = 0.0233 (calculated in radians)
Therefore, the shape factor according to Steinbrenner;
IS = F1 + [(1 – 2μs)/(1 – μs)] × F2 = 0.5842 + [(1 – (2 × 0.3) / (1 – 0.3)] × 0.0233 = 0.5975
From chart, let us obtain the foundation embedment factor (If);
Df/B = 0.9/1.8 = 0.5
L/B = 2.7/1.8 = 1.5
From the chart, say If = 0.79
Inputting all the parameters into the elastic settlement equation given in (1)
Se = qo α × B’ × ((1- μs2)/Es) × Is × If
Se = 145 × 4 × 0.9 × ((1 – 0.32)/10526.667) × 0.5975 × 0.79 = 0.0213m = 21.3 mm
This gives the elastic settlement at the centre of the footing. A lot of modifications and other proposals have been made by scholars over years due to improved research, and we will keep posting them as time goes on.
Keep visiting www.structville.com and tell your folks about it.