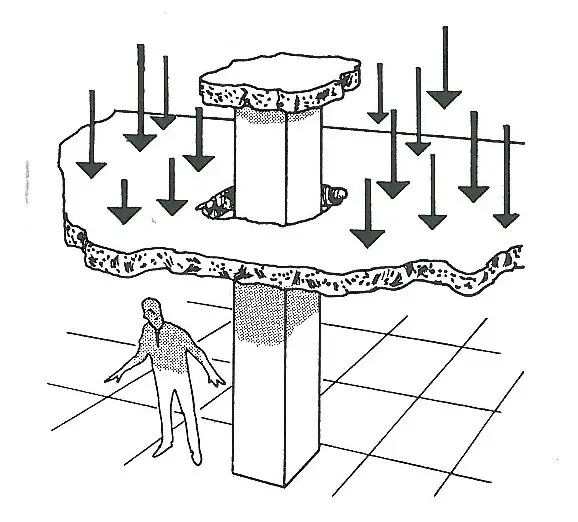
Punching Shear in Flat Slabs: A Design Example to Eurocode 2

Punching shear failure occurs in a slab when the magnitude of a concentrated load (such as that from a column) exceeds the shear strength or resistance of the slab or the column punches through the slab. The failure plane is located at a certain distance from the perimeter of the column and has a funnel-shaped failure pattern. The design for punching shear resistance in flat slabs normally involves controlling the thickness of the slab or providing punching shear reinforcement.

Generically, punching is a three-dimensional, brittle failure mechanism leading to a truncated cone that separates from the slab. The shear crack develops from tangential flexural cracks and propagates into the direction of the compression zone near the column edge constricting the circumferential compression ring with increasing loads. Once the punching shear resistance is reached the shear crack intersects the uncracked compression ring leading to a sudden penetration of the column into the slab.

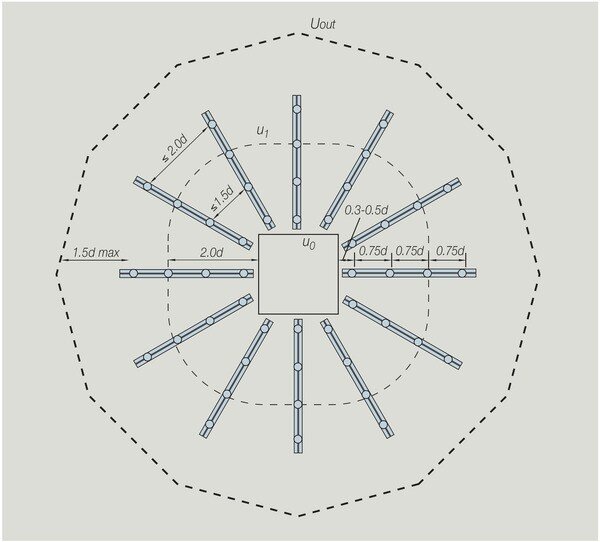
The recommendations found in BS EN 1992 (Eurocode 2) are usually followed when designing punched shear reinforcement. To assess whether punched shear reinforcement is necessary, the shear stress in the concrete is computed at the column face and at the fundamental control perimeter u₁ (2d from the column face).

The position of the outside control perimeter where shear reinforcement is no longer needed (u_out) is then determined if reinforcement is necessary. Shear studs are placed starting at 0.3d or 0.5d from the column face to within 1.5d of the outer control perimeter (u_out), with intermediate studs spaced at 0.75d intervals.

The most cost-effective approach will often be a radial arrangement, with rails spaced either 30° or 45° apart. To meet this requirement, extra secondary rails are installed as necessary. The tangential spacing between studs is kept to within 1.5d for studs inside the basic control perimeter (u₁) and 2d for studs outside the basic control perimeter.

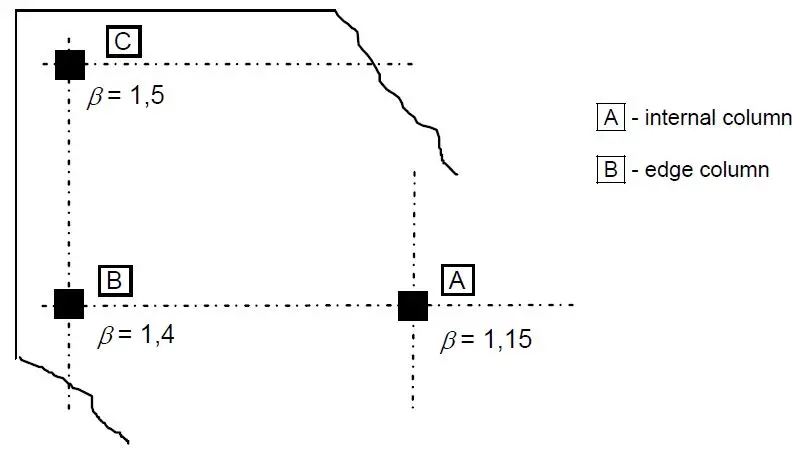
The suggested values from BS EN 1992 can be used to design shear load V_Ed for internal, edge, and corner columns where lateral stability does not depend on frame action between slabs and columns and where neighbouring spans differ by less than 25%.

Design for punching shear should take moment transfer into account at the intersection of the column and slab. The design punching shear can be obtained for structures whose lateral stability is not dependent on the frame action between the slab and columns and where adjacent spans do not differ in length by more than 25% by increasing V_Ed by 1.15 for internal columns, 1.4 for edge columns, and 1.5 for corner columns.

Generally, the following checks should be carried out: 

• Ensure that maximum punching shear stress is not exceeded, i.e. v_Ed < v_Rd,max at the column perimeter
• Determine whether punching shear reinforcement is required, i.e. whether v_Ed > v_Rd,c at the basic perimeter, u₁
• Determine whether punching shear reinforcement is required, i.e. whether v_Ed > v_Rd,c at at successive perimeters to establish u_out    = the length of the perimeter where v_Ed = v_Rd,c. Perimeters within 1.5 d from u_out need to be reinforced.

Where required provide reinforcement such that v_Ed ≤ v_Rd,cs.

where

v_Ed  =    applied shear stress. The shear force used in the verification should be the effective force taking into account any bending moment transferred into the slab (see above)

v_Rd,max = design value of the maximum punching shear resistance, expressed as a stress
v_Rd,c = design value of punching shear resistance of a slab without punching shear reinforcement, expressed as a stress
v_Rd,cs    = design value of punching shear resistance of a slab with punching shear reinforcement, expressed as a stress.

v_Rd,cs = 0.75 v_Rd,c + 1.5 (d/s_r)A_sw f_ywd,ef (1/u₁d)sin a

where:

A_sw = area of shear reinforcement in one perimeter around the column (subject to A_sw,min)
s_r    = radial spacing of perimeters of shear reinforcement
f_ywd,ef = effective design strength of reinforcement (250 + 0.25d) ≤ f_ywd
d    = mean effective depth in the two orthogonal directions (in mm)
u₁   = basic control perimeter at 2d from the loaded area
sin a = 1.0 for vertical shear reinforcement

Where required each perimeter should have
A_sw = (v_Ed – 0.75 v_Rd,c)s_r u₁/(1.5 f_ywd,ef)

The punching shear resistance of a slab should be assessed for the basic control section (see Figure 6.12). The design punching shear resistance [MPa] may be calculated as follows:

v_Rd,c = C_Rd,c k (100 ρ_l f_ck)^1/3 + k₁ σ_cp   ≥ (v_min + k₁ σ_cp)

where:
f_ck is the characteristic compressive strength of concrete, see Table 3.1
k= 1 + √200/d   ≤ 2.0
where d is the effective depth, in [mm]ρ_l= (ρ_ly⋅ρ_lz)^1/2 ≤ 2%
ρ_ly, ρ_lz are longitudinal reinforcement ratios in y- and z- directions respectively. Their values should be calculated as mean values taking into account a slab width equal to column width plus 3d each side σ_cp= (σ_cy + σ_cz)/2,
where σ_cy, σ_cz are the normal concrete stresses in the critical section in y- and z- directions (in [MPa], positive if compression):
σ_cy = N_Ed,y / A_cy and σ_cy = N_Ed,z / A_cz
N_Ed,y, N_Ed,y are the longitudinal forces across the full bay for internal columns and the longitudinal force across the control section for edge columns. The force may be from a load or prestressing action.
A_cy, A_cz are the areas of concrete according to the definition of N_Ed,y, N_Ed,y respectively
C_Rd,c is a Nationally Determined Parameter, see § 6.4.4 (1)
v_minis a Nationally Determined Parameter, see § 6.4.4 (1), or (6.3N) for the calculation of v_min following the Eurocode recommendation
k₁ is a Nationally Determined Parameter, see § 6.4.4 (1).

Punching Shear Design Example

For the flat slab with the general arrangement as shown below, let us design the punching shear for column B1 given the following design information;

Ultimate axial force on column V_Ed = 400 kN
Thickness of slab = 250 mm
Dimension of column = 450 x 230 mm
Reinforcement of slab in the longer direction = H16@150mm (A_s,prov = 1340 mm²)
Reinforcement of slab in the shorter direction = H16@175mm (A_s,prov = 1149 mm²)
Grade of concrete = C30
Yield strength of reinforcement = 500 Mpa
Concrete cover to slab = 25mm

Solution

Effective depth of slab in y-direction d_y = 250 – 25 – (16/2) = 217 mm
Effective depth of slab in x-direction d_x = 250 – 25 – 16 = 209 mm

ρ_ly = (1340) / (1000 × 217) = 0.00617 (reinforcement ratio)
ρ_lx = (1149) / (1000 × 209) = 0.00549 (reinforcement ratio)

(a) Check shear at the perimeter of the column

V_Ed = β V_Ed/(u₀d) < V_Rd,max

From figure 6.21N of EN 1992-1-1;
β = 1.40
d = (217 + 209)/2 = 213 mm

u₀ = c₂ + 3d < c₂ + 2c₁ For edge columns (clause 6.4.5(3))

u₀ = 230 + (3 × 213) <  (230 + 2 × 450)
u₀ = 869 mm
V_Ed = 1.40 × 400 × 1000/(869 × 213) = 3.025 MPa
V_Rd,max = 0.5 ν f_cd
= 0.5 × 0.6(1 – f_ck/250) × α_cc f_ck/γ_m
= 0.5 × 0.6(1 – 30/250) × 1.0 × (30 /1.5) = 5.28 MPa
V_Ed < V_Rd,max …OK

(b) Check shear at u₁, the basic control perimeter
V_Ed = β V_Ed/(u₁d) < V_Rd,c

β,V_Ed as before
u₁ = c₂ + 2c₁ + π × 2d
u₁ = 230 + (2 × 450) + (π × 2 × 213) = 2468 mm

V_Ed = 1.4 × 400 × 1000/(2468 × 213) = 1.065 MPa
V_Rd,c = 0.12 k(100 ρ_l f_ck)^1/3

k = 1 + (200/d)^1/2 = 1 + (200/213)^1/2 = 1.969

ρ_l = (ρ_lyρ_lx)^1/2 = (0.00617 × 0.00549)^1/2 = 0.00582

V_Rd,c = 0.12 × 1.969(100 × 0.00582 × 30)^1/3 = 0.613 MPa

V_Ed > V_Rd,c ?
1.065 MPa > 0.613 MPa … Therefore punching shear reinforcement required

NA check:
V_Ed ≤ 2.0V_Rd,c at basic control perimeter
1.06 MPa ≤ 2 × 0.613 MPa = 1.226 MPa – OK

(c) Perimeter at which punching shear no longer required
u_out = β V_Ed/(dV_Rd,c)
= 1.4 × 400 × 1000/(213 × 0.613) = 4289 mm

Rearrange: u_out = c₂ + 2c₁ + π r_out
r_out = (u_out – (c₂ + 2c₁))/π
r_out = (4289 – 1130)/π = 1005 mm

Position of outer perimeter of reinforcement from column face:
r = 1005 – 1.5 × 213 = 686 mm

Maximum radial spacing of reinforcement:
s_r,max = 0.75 × 213 = 159.75 mm, say 150 mm

(d) Area of reinforcement
A_sw ≥ (V_Ed – 0.75V_Rd,c)s_ru₁/(1.5f_ywd,ef)
f_ywd,ef = (250 + 0.25d) = 303 MPa

A_sw ≥ (1.065  – 0.75 × 0.613) × 150 × 2468/(1.5 × 303)
≥ 492 mm² per perimeter

Provide 7H10 (A_sprov = 549 mm² per perimeter)

Within the u₁ perimeter the link spacing around a perimeter,
s_t ≤ 1.5d = 1.5 × 213 = 319.5 mm

Outside the u₁ perimeter the link spacing around a perimeter,
s_t ≤ 2d = 426 mm
Use say s_t,max = 300 mm

Minimum area of a link leg:
A_sw,min ≥ [0.053 s_r s_t sqrt(f_ck)] /f_yk = (0.053 ×  150 ×  300 ×  √30) / 500
≥ 26 mm²

Use H10s (78.5 mm²) and 7 per perimeter.
@ 300 mm tangential spacing and @150 mm radial spacing

Thank you for visiting Structville today and God bless you.