Flat slabs are slabs are two-way concrete slabs that are supported directly by columns without floor beams. Therefore, they offer economical solutions to larger floor spans in reinforced concrete buildings. The columns supporting the slab panel may or may not have drop panels.
Drop panels are particularly advantageous in situations where substantial negative moments occur at supports or where punching shear stresses are critical and the use of punching reinforcement is undesirable.
There are many advantages of flat slabs such as increased headroom, easier flow of mechanical and electrical services, ease in construction of formwork, faster construction etc. Unlike traditional beam and slab systems, flat slabs eliminate the use of floor beams, resulting in a cleaner, more open space.
Analysis of Flat Slabs
The following methods are usually employed in the analysis of flat slabs:
- simplified coefficient approaches,
- equivalent frame analysis,
- yield line theory,
- grillage analysis, and
- finite element methods.
The application of simplified coefficients is subject to specific conditions outlined in Annex I of BS EN 1992-1-1. Yield line and finite element methods are particularly well-suited for computer-based analysis. Given this, this discussion will concentrate on the use of simplified coefficients.
In the Eurocodes, the analysis of flat slab is the same as that recommended in BS 8110. According to clause 3.7.2.7 of BS 8110, the simplified method can be used for flat slabs that the lateral stability is not dependent on the slab and columns provided that the following conditions are met;
(1) The slab is loaded with a single load case of all the panels loaded with maximum ultimate load. This means that the following requirements must be satisfied (clause 3.5.2.3);
(a) The area of each bay exceeds 30 m2
(b) The ratio of the characteristic imposed load to the dead load does not exceed 1.25
(c) The imposed load does not exceed 5 kN/m2
(2) There are at least three rows of approximately equal panels in the direction being considered
(3) Moments at supports can be reduced by 0.15Fhc
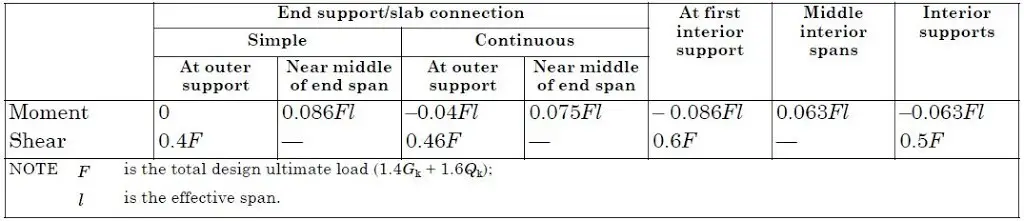
Design Example of Flat Slab
In this article, we are going to analyse gridline 2 (same as gridline 5) of the flat slab general arrangement that is given above with the following data;
The thickness of slab = 230 mm (governed by deflection requirements)
fck = 30 Mpa
fyk = 500 Mpa
Imposed load = 3 kN/m2
Concrete cover = 30 mm
Size of columns = 300 x 300 mm
Load Analysis
Permanent Actions
Self weight = 0.23 × 25 = 5.75 kN/m2
Finishes = 1.2 kN/m2
Partition allowance = 1.2 kN/m2
Total permanent actions gk = 8.15 kN/m2
Variable Actions
Imposed floor load qk = 3 kN/m2
Total load on the floor F = 1.35gk + 1.5qk = 1.35(8.15) + 1.5(3) = 15.5 kN/m2
Effective span of the slab = 6500 – 2(300/2) + 2(230/2) = 6430 mm
Width of bay = 6500 mm
Width of column strip = 2(lx/4)= 2(6500/4) = 3250 mm
Width of middle strip = 6500 – 1625 – 1625 = 3250 mm
F = 15.5 × 6.5 × 6.5 = 654.875 kN
A little consideration will show that the slab under consideration met the conditions for use of coefficients.
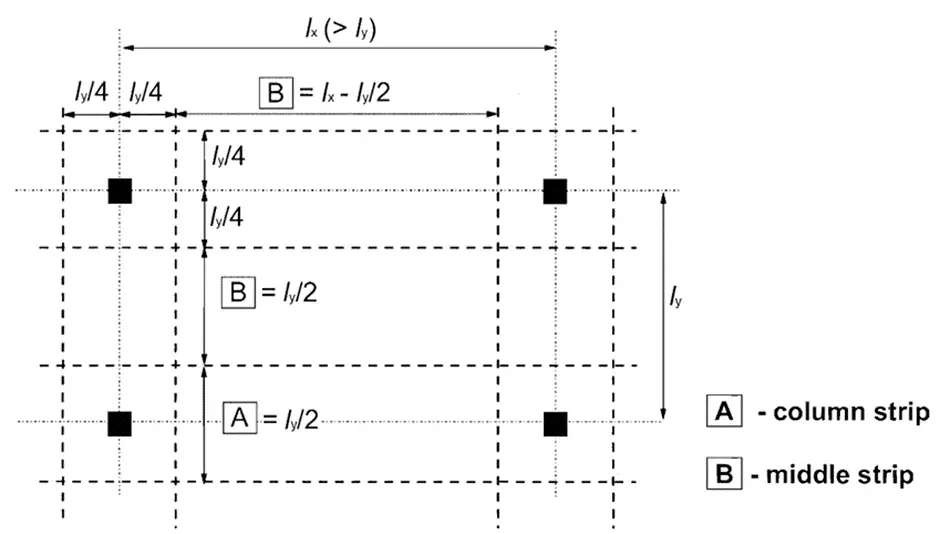
For reference on how the panel was divided into middle and column strips, see Figure 3.12 of BS 8110-1:1997.
Bending Moments (In the longitudinal direction)
Sagging – First Span
M = 0.086 × 654.87 × 6.43 = 362.13 kNm
Hogging – First interior support
M = -0.086 × 654.87 × 6.43 = -362.13 kNm
The apportionment of moments between column strips and middle strips is shown in Table 2:
| Hogging | Sagging | |
| Column strip | 70% | 50% |
| Middle strip | 30% | 50% |
(Column Strip)
Hogging moment (Support B and C)
MEd = 0.7 × (362.13/3.25) = -77.99 kNm/m
Sagging moment:
MEd = 0.5 × (362.13/3.25) = 55.71 kNm/m
(Middle Strip)
Hogging moment (Support B and C)
MEd = 0.3 × (362.13/3.25) = -33.427 kNm/m
Sagging moment:
MEd = 0.5 × (362.13/3.25) = 55.71 kNm/m
Structural Design – Flexure: column strip and middle, sagging
MEd = 55.71 kNm/m
d = h – Cc – ϕ/2
Assuming ϕ16mm bars will be employed for the construction
d = 230 – 30 – 8 = 192 mm; b = 1000mm (designing per unit width)
k = MEd/(fckbd2) = (55.71 × 106)/(30 × 1000 × 1922) = 0.086
Since k < 0.167 No compression reinforcement required
z = d[0.5 + √(0.25 – 0.882k)]
z = d[0.5 + √(0.25 – 0.882 × 0.086)] = 0.917d = 0.917 × 192 = 176.12 mm
As1 = MEd/(0.87fykz) = (55.71 × 106)/(0.87 × 500 × 176.12) = 727 mm2/m
Provide H16mm @ 200 mm c/c BOT (ASprov = 1005 mm2/m)
Check the minimum area of steel required;
fctm = 0.3 × fck2⁄3 = 0.3 × 302⁄3 = 2.89 N/mm2 (Table 3.1 EC2)
As,min = 0.26 × fctm/fyk × b × d = 0.26 × 2.89/500 × 1000 × 192 = 289 mm2/m
Check if As,min < 0.0013 × b × d (250 mm2/m)
Since, As,min = 250 mm2, the provided reinforcement is adequate.
Check for deflection
We check for deflection of flat slabs at the long span of the slab
Allowable L/d = N × K × F1 × F2 × F3 ≥ Actual L/d
K = 1.2 for flat slabs
ρ = As,req/bd = 727/(1000 × 192) = 0.003786 > 10-3√fck (0.00547)
Since ρ > ρ0
l/d = [11 + 1.5√fck(ρ0/(ρ – ρ’)) + 0.0833√fck(ρ0/ρ)0.5] if ρ > ρ0
ρ0/ρ= 0.00547/0.003786 = 1.44
N = [11 + 1.5√(30) × 1.444 + 0.0833√30 × (1.444)0.5] = 11 + 11.86 + 0.548 = 23.4
F1 = 1.0 (beff/bw = 1.0)
F2 = 1.0 (no brittle partitions)
F3 = 310/σs ≤ 1.5
where:
σsu = (500/1.15) × (8.15 + 0.3 × 3)/15.5 = 253.856 MPa
σs = σsu × (As,req/As,prov) = 253.856 × (727/1005) = 183.6 N/mm2
βs = 310/183.6 = 1.688 > 1.5 (take 1.5)
Therefore allowable L/d = 23.4 × 1.2 × 1.0 × 1.0 × 1.5 = 42.12
Actual L/d = 6430/192 = 33.49
Therefore, deflection is okay.
Flexure: column strip, hogging
MEd = 77.99 kNm/m
k = MEd/(fckbd2) = (77.99 × 106)/(30 × 1000 × 1922) = 0.0705
Since k < 0.167 No compression reinforcement required
z = d[0.5 + √(0.25 – 0.882k)]
z = d[0.5 + √(0.25 – 0.882 × 0.0705)] = 0.933d = 0.933 × 192 = 179.2 mm
As1 = MEd/(0.87fykz) = (77.99 × 106)/(0.87 × 500 × 179.2) = 1000 mm2/m
Provide T16mm @ 175 mm c/c Top (ASprov = 1149 mm2/m)
(c) Flexure: Middle strip, hogging
MEd = 33.43 kNm/m
k = MEd/(fckbd2) = (33.43 × 106)/(30 × 1000 × 1922) = 0.030
Since k < 0.167 No compression reinforcement required
z = d[0.5 + √(0.25 – 0.882k)]
z = d[0.5 + √(0.25 – 0.882 × 0.030)] = 0.95d = 0.95 × 192 = 182.4 mm
As1 = MEd/(0.87fykz) = (33.43 × 106)/(0.87 × 500 × 182.4) = 421 mm2/m
Provide T12mm @ 200 mm c/c Top (ASprov = 565 mm2/m)
Perpendicular to edge of slab at edge column
Design transfer moment to column Mt = 0.17 bed2fck
be = cz + y = 300 + 300 = 600 mm
Mt = 0.17 × 600 × 1922 × 30 × 10−6 = 112.8 kNm
k = MEd/(fckbd2) = (112.8 × 106)/(30 × 600 × 1922) = 0.1699
z = d[0.5 + √(0.25 – 0.882k)]
z = d[0.5 + √(0.25 – 0.882 × 0.1699)] = 0.82d = 0.82 × 192 = 157.44 mm
As1 = MEd/(0.87fykz) = (112.8 × 106)/(0.87 × 500 × 157.44) = 1647 mm2/m
This reinforcement to be placed within cx + 2cy = 900 mm
Try H16T1 U-bars in pairs @ 100 (Asprov = 2010 mm2) local to column (max. 200 mm from column)
Punching Shear Check
See worked example on punching shear verification of flat slabs.





A great professional is a component consultant; salesman, Express of Arizona and negotiator real estate property residence houses for sale near my location! Arizona actual estate's individuality is vibrant, amusing, thoughtful and unbelievably consultant. As he by no means supplied right through to finding us the best home although we had been ready to chuck inside the delicate soft towel a lot more than!
can you show the detailing of a typical flat slab
Great stuff. Can you kindly show the detailing of Flat slab
Thank you
good