The provision of partitions on suspended slabs of residential, commercial, or industrial buildings is widespread in the construction industry. Spaces in a building can be demarcated using a variety of partition materials such as sandcrete blocks, bricks, gypsum dry walls, timber stud walls, metal lath, etc. These partitions exert additional loads on a suspended slab, and should be accounted for in the design of the slab. This is necessary especially when there is no beam or wall directly under the slab supporting the partition.
It is important to note that wall and partition loads insist on suspended slabs as line loads instead of uniformly distributed loads. It is more complex to analyse line loads on plates than uniformly distributed loads. Therefore during designs, engineers usually attempt to represent line loads with equivalent uniformly distributed loads to make the computational effort easier.

There are established guides in the building code for assessing all types of loads that a building might be subjected to, and partition loads is not an exception. Typically in the design of reinforced concrete solid slabs, a partition allowance of between 1.00 kN/m2 to 1.5 kN/m2 is usually made during the analysis of dead loads (permanent actions). This is usually sufficient to allow for all lightweight movable partitions that may be placed on the slab later.
According to clause 6.3.1.2 of EN 1991-1-1:2002, provided that a floor allows a lateral distribution of loads, the self-weight of movable partitions may be taken into account by a uniformly distributed load qk which should be added to the imposed loads of floors obtained from Table 6.2. This defined uniformly distributed load is dependent on the self-weight of the partitions as follows:
- for movable partitions with a self-weight < 1.0 kN/m wall length: qk = 0.5 kN/m2
- for movable partitions with a self-weight > 1 ≤ 2.0 kN/m wall length: qk = 0.8 kN/m2
- for movable partitions with a self-weight > 2 ≤ 3.0 kN/m wall length: qk = 1.2 kN/m2
However, full design consideration should be taken for heavier partitions, accounting for the locations and directions of the partitions and the structural forms of the floors.
According to BS 6399 Part 1, when the position of the wall load is not known, the equivalent uniformly distributed load that is added to the slab load should be 0.33wp (kN/m2), where wp is the weight of the wall (kN/m).
However, when the direction of the partition is normal to the span of the slab, the equivalent uniformly distributed load is given by 2wp/L for simply supported slabs and 3wp/2L for continuous slabs (Where L is the span of the slab normal to the wall load).
Said et al (2012) used finite element analysis and multiple linear regression to derive a general relation between line loads acting on two-way slab system and the equivalent uniformly distributed loads. According to them;
WUDL/WLine = 0.32193 + 0.00473α – 0.10175(L2/L1) ——– (R2 = 0.8327)
Where;
WUDL/WLine is the ratio of equivalent uniformly distributed load to actual line load,
α is the relative ratio of the stiffness of beam to slab,
L2/L1 is the aspect ratio of the slab.
Therefore, from the statistical relationship above, when the value of the line load is known, the equivalent UDL that will produce comparable bending moment values can be obtained using the aspect ratio of the slab and the ratio of the stiffness of the supporting beams to the slab.
Partitions such as sandcrete blocks exert a significant magnitude line load on reinforced concrete solid slabs. For a 225mm hollow block, the unit weight is about 2.87 kN/m2. For a 12 mm thick plaster on both sides, the total weight of finishes is about 0.6 kN/m2. This brings the total unit weight of the block to about 3.47 kN/m2, which is usually approximated to 3.5 kN/m2.
Therefore, for a wall height of 3m, the equivalent line load exerted on the supporting slab or beam is 3.5 kN/m2 × 3m = 10.5 kN/m.
So many structural engineering software design packages have the option of applying line loads directly on slabs. For software like Staad Pro, it may not be possible to assign line loads directly on plates, however a dummy beam of negligible stiffness can be used to transfer the line load to the slab.
Example on Partition Load Modelling
To demonstrate the effects of line loads from block wall, let us consider a 150 mm thick 5m x 6m two-way slab that is simply supported at all edges by a 450 mm x 225mm beam. The slab is supporting a line load of 10.5 kN/m coming from a 225 mm thick block wall placed at the centre parallel to the short span as shown below.
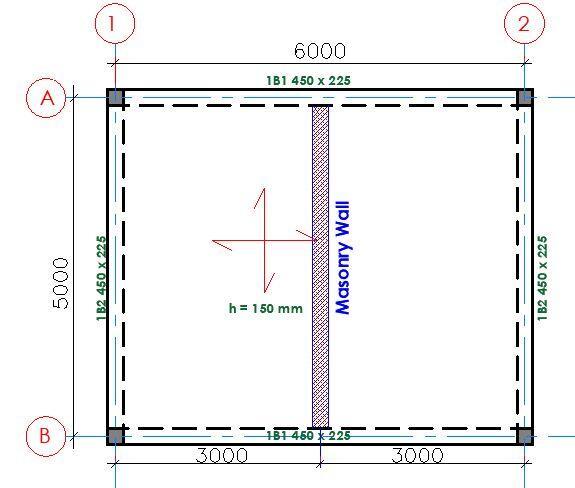
We are going to consider several scenarios;
(a) When the slab is loaded directly with the line load (w = 10.5 kN/m)
(b) When the line load is represented with equivalent UDL given by 0.33wp = 0.33 × 10.5 = 3.15 kN/m2
(c) When the line load is represented with an equivalent UDL given by 2wp / L = (2 × 10.5)/6 = 3.5 kN/m2
(d) When the line load is represented with an equivalent UDL by Said et al (2012);
WUDL/WLine = 0.32193 + 0.00473α – 0.10175(L2/L1)
Stiffness of beam = (0.225 × 0.453)/12 = 1.70859 × 10-3 m4
Stiffness of slab = (1 × 0.153)/12 = 2.8125 × 10-4 m4
α = (1.70859 × 10-3)/(2.8125 × 10-4) = 6.075
L2/L1 = 6/5 = 1.2
WUDL/WLine = 0.32193 + 0.00473(6.075) – 0.10175(1.2) = 0.2279
Therefore WUDL = 0.2279WLine = 0.2279 × 10.5 = 2.392 kN/m2
Analysis Results
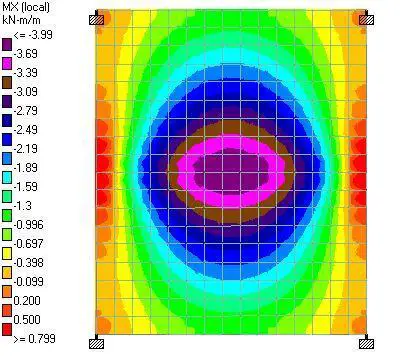
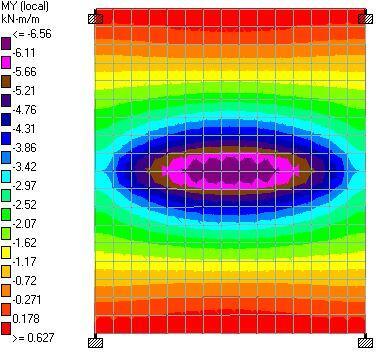
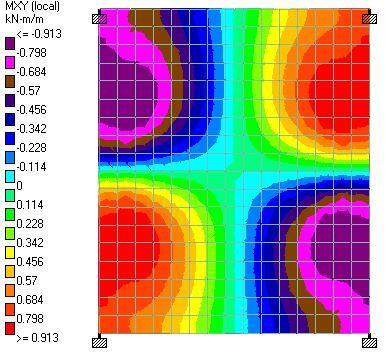
(a) When the slab is loaded directly with the line load (w = 10.5 kN/m)
(b) When the line load is represented with equivalent UDL (we = 3.15 kN/m2)
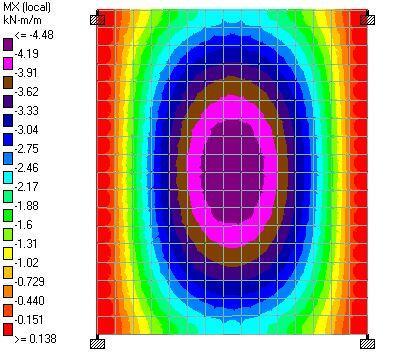
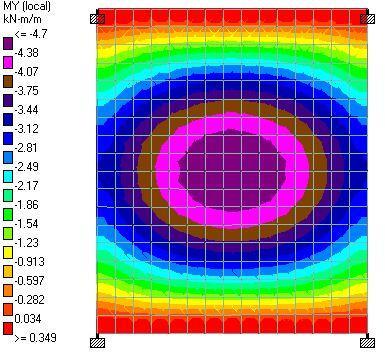
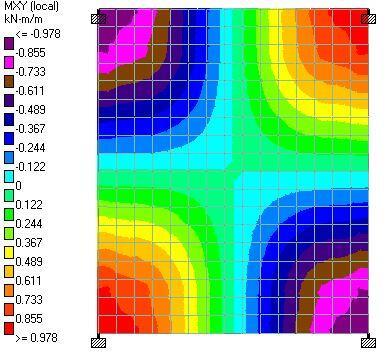
(c) When the line load is represented with equivalent UDL (we = 3.5 kN/m2)
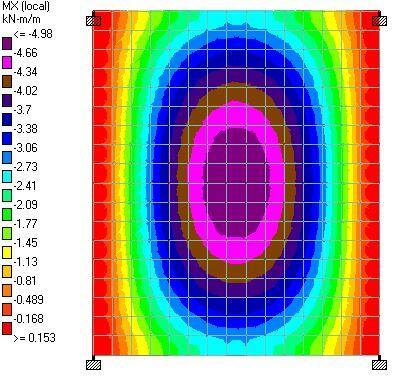
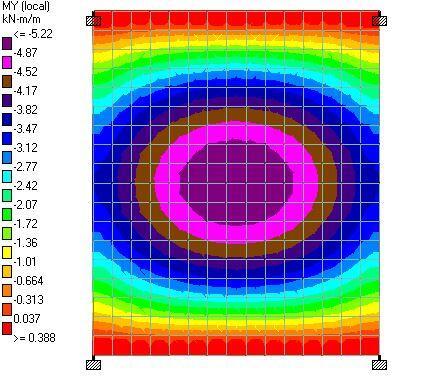
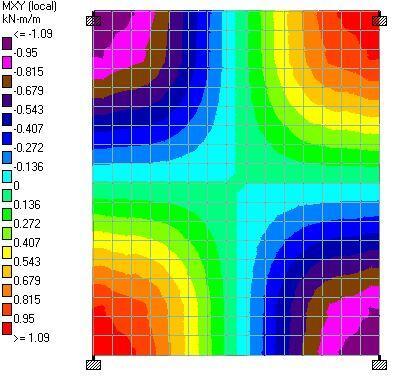
(d) When the line load is represented with equivalent UDL (we = 2.392 kN/m2)
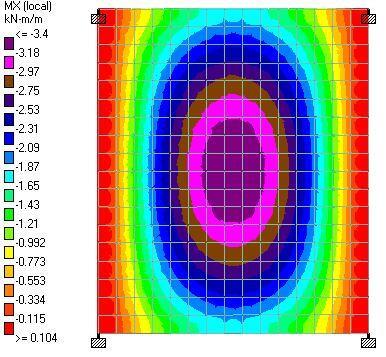
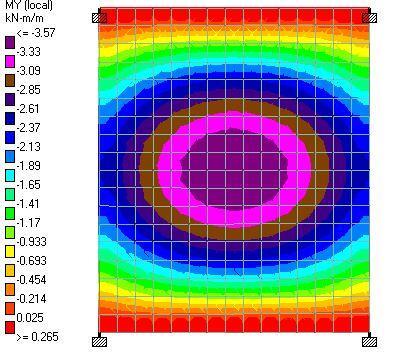
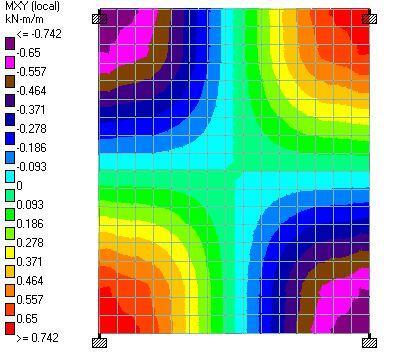
| Analysis Method | Mx (sagging) | Mx (hogging) | My (sagging) | Mx (hogging) | Mxy |
| Line Load | 3.99 kNm | 0.799 kNm | 6.65 kNm | 0.627 kNm | 0.913 kNm |
| 0.33wp = 3.15 kN/m2 | 4.48 kNm | 0.138 kNm | 4.7 kNm | 0.349 kNm | 0.978 kNm |
| 2wp / L = 3.5 kN/m2 | 4.98 kNm | 0.153 kNm | 5.22 kNm | 0.388 kNm | 1.09 kNm |
| WUDL = 0.2279WLine = 2.392 kN/m2 | 3.4 kNm | 0.104 kNm | 3.57 kNm | 0.265 kNm | 0.742 kNm |
From the analysis result, it can be seen that none of the proposed equations was able to capture the effect of the line load adequately. Therefore, when heavy wall loads are to be supported on suspended slabs, the line load should be properly modelled on the slab instead of being converted to equivalent uniformly distributed load.
References
Said A. A, Obed S. R., and Ayez S. M. (2012): Replacement of Line Loads acting on slabs to equivalent uniformly Distributed Loads. Journal of Engineering 11(18):1193 – 1200










how do you verify this with manual calculation?