Analysis and Design of a Network of Interacting Primary and Secondary Beams

In some construction cases, it is desirable to have large uninterrupted floor areas, and in such cases, the presence of internal columns has to be minimal. This can be achieved to some extent by using a network of interacting reinforced primary and secondary beams.

This feature is desirable in buildings like conference halls, auditoriums, stadiums, churches, dance halls, and all buildings where there is a need for a performing stage, and spectators. The structural implication of such features is usually the presence of long spans elements, and a lot of solutions already exist for such constructions.

It is already a well-known fact that the use of conventional reinforced concrete beams becomes more uneconomical as the construction span increases. This is primarily because the predominant in beams are bending moment and shearing forces, which are all functions of the length of the beam.

To accommodate these internal forces during design usually calls for an increase in the size of the member sections to satisfy ultimate and serviceability limit state requirements. This further adds to the total dead load of the structure, which is conventionally undesirable for economical reasons. A better solution for handling the problem of long-span construction is the use of structural forms like trusses and arches.

Trusses are arrangements of straight members connected at their ends. The members are arranged to form a triangulated system to make them geometrically unchangeable, and hence will not form a mechanism. They resist loads by developing primarily axial forces in their members especially if the ends of the members are pinned together. In typical trusses, loads are applied only at the joints.

Trusses provide practical and economical solutions to engineering problems, and can efficiently span greater lengths than beams due to the development of predominantly axial forces in the members. Trusses can be found on the roof of buildings, bridges etc. The picture above shows a model of a truss bridge.

Arches are also widely used in modern engineering due to their ability to cover large spans and their attractiveness from an aesthetic point of view. The greater the span, the more an arch becomes more economical than a truss. Materials of the modern arches are concrete, steel, and timber. Arches are mainly classified as three-hinged, two-hinged, and arch with fixed supports.

Arches carry most of their loads by developing compressive stresses within the arch itself and therefore in the past were frequently constructed using materials of high compressive strength and low tensile strength such as stones and masonry. They may be constructed in a variety of geometries; semi-circular, parabolic or even linear where the members comprising the arch are straight. The picture below shows the New River Gorge Arch steel bridge near Fayetteville, West Virginia USA.

Network of Primary and Secondary Beams

However, when it is desirable to have a relatively large hall devoid of internal columns, a network of interacting reinforced primary and secondary beams can be employed as alternatives to other solutions. A little consideration will show that in such cases, it is possible that the cost of adopting such a method of construction can be cheaper than that of trusses or arches.

No serious expertise is required on the part of the contractor when constructing a system of primary and secondary beams since very familiar construction processes are adopted. The logistics and expertise associated with assembling trusses and arches can offset the cost of larger concrete sections and reinforcing bars. Therefore, the knowledge of how this analysis and design can be carried out is necessary for the engineering community.

In the simplest term, a network of primary and secondary beams involves supporting a beam (called a secondary beam) on another beam (called a primary beam) instead of a column or wall. The position of support can be at the ends or at any intermediate location of the secondary beam. By implication, it is very usual for the secondary beam to be shallower than the primary beam (but sometimes this may not the case).

The choice of selecting the axis of the primary beam usually depends on the length. The beam with the shorter span is preferably the primary beam, so as to easily control strength and deflection. The analysis often involves loading and analysing the secondary beams first, and then the support reactions are transferred to the primary beam as concentrated loads. A primary beam is often supported on a column or wall.

In the analysis of a secondary beam, it should be borne in mind that the supports of the beam are not entirely rigid, since the primary beams supporting the secondary beams will undergo some deflection. This can be taken into account by representing the supports of secondary beams with springs, whose stiffness is equal to the stiffness of the primary beams.

Design Example

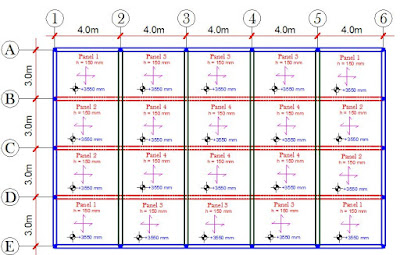
In the example below, a hall of 12m x 20m with the general arrangement shown below has been analysed and designed. In the example below, we are going to analyse only the internal beams, and we are going to consider all the spans to be fully loaded at ultimate limit state.

From the figure below, the secondary beams are shown in red (dotted lines) while the primary beams are shown in green. Every beam under consideration is supported by columns at the first and last supports. No internal column exists anywhere in the hall, and it is also assumed that the internal beams are not carrying block work loads, but light moveable partitions (drywalls).

With the general arrangement shown above, let us attempt to design some of the secondary and primary beams.

Design Data
Thickness of slab = 150 mm
All secondary beams = 450mm x 230mm
All primary beams = 900 mm x 400mm
Density of concrete = 25 kN/m³
Design compressive strength of concrete = 35 N/mm²
Yield strength of all reinforcements = 460 N/mm²
Concrete cover to slab = 25mm
Concrete cover to beams = 30mm
ULS Combination = 1.35g_k + 1.5q_k
SLS Combination = 1.0g_k + 1.0q_k
Imposed load = 5 kN/m² (NA to BS EN 1991-1-1:2002)
Building Category = Category C4

Structural Design of the secondary beams

Flexural design of span 1-2 and span 5-6
M_Ed = 53.95 kNm
Effective depth (d) = h – C_nom – ϕ/2 – ϕ_links
Assuming ϕ16 mm bars will be employed for the main bars, and ϕ8mm bars for the stirrups (links)
d = 450 – 30 – 8 – 8 = 404 mm

Effective flange width of the beams (T-beams)
b_eff = b_w + b’
Where b’ = 0.2(a_w + l_o) ≤ 0.4l_o ≤ 1.0a_w (for T-beams)
b_w = web width;
a_w = Clear distance between the webs of adjacent beams = 3000 – 230 = 2770 mm
l_o = The distance between points of zero moment on the beam = 0.85L = 0.85 × 4000 = 3400mm
Therefore in this case, b’ = 0.2(2770 + 3400) = 1234 mm ≤ 0.4l_o
Therefore b_eff = 230 + 1234 = 1464mm

k = M_Ed/(f_ckb_effd²) = (53.95 × 10⁶)/(35 × 1464 × 404²) = 0.00645
Since k < 0.167, no compression reinforcement required
z = d[0.5 + √(0.25 – 0.882K)] = z = d[0.5+ √(0.25 – 0.882(0.00645))] = 0.95d
A_s1 = M_Ed/(0.87f_yk z) = (53.95 × 10⁶)/(0.87 × 460 × 0.95 × 404) = 351.244 mm²
Provide 2X16 mm BOT (AS_prov = 402 mm²)

To calculate the minimum area of steel required;
f_ctm = 0.3 × f_ck^(2⁄3) = 0.3 × 35^(2⁄3) = 3.20996 N/mm² (Table 3.1 EC2)
A_Smin = 0.26 × f_ctm/f_yk × b × d = 0.26 × (3.20996/460) × 230 × 404 = 168.587 mm²
Check if AS_min < 0.0013 × b × d (120.796 mm²)
Since, AS_min = 168.587 mm², the provided reinforcement is adequate.
Deflection checks were found to be satisfactory.

Flexural Design of Support 2
M_Ed = 72.89 kNm
k = M_Ed/(f_ckb_wd²) = (72.89 × 10⁶)/(35 × 230 × 404²) = 0.055
Since k < 0.167 No compression reinforcement required
z = d[0.5+ √(0.25 – 0.882K) ] = z = d[0.5+ √(0.25 – 0.882(0.055)) ] = 0.949d

A_s1 = M_Ed/(0.87f_yk z) = (72.89 × 10⁶)/(0.87 × 460 × 0.949 × 404) = 475 mm²
Provide 3X16mm TOP (A_Sprov = 603 mm²)

Shear Design Support 1
Ultimate shear force V_Ed = 68.33 kN
V_Rd,c = [C_Rd,c.k.(100ρ₁ f_ck)^(1/3) + k₁.σ_cp]b_w.d ≥ (V_min + k₁.σ_cp) b_w.d

Where;
C_Rd,c = 0.18/γ_c = 0.18/1.5 = 0.12
k = 1 + √(200/d) = 1 + √(200/404) = 1.704 > 2.0, therefore, k = 1.702
V_min = 0.035k^(3/2) f_ck^(1/2) = V_min = 0.035 × 1.702^(3/2) × 35^(1/2) = 0.4598 N/mm²
ρ₁ = As/bd = 402/(230 × 404) = 0.004326 < 0.02; K₁ = 0.15

σ_cp = N_Ed/Ac < 0.2f_cd (Where N_Ed is the axial force at the section, Ac = cross sectional area of the concrete), f_cd = design compressive strength of the concrete.)
Take N_Ed = 0

V_Rd,c = [0.12 × 1.703(100 × 0.004326 × 35 )^(1/3)] 230 × 404 = 46977.505 N = 46.977505 KN
Since V_Rd,c (46.977505 KN) < V_Ed (68.33 KN), shear reinforcement is required.

The compression capacity of the compression strut (V_Rd,max) assuming θ = 21.8° (cot θ = 2.5)
V_Rd,max = (b_w.z.v₁.f_cd)/(cot⁡θ + tanθ)
V₁ = 0.6(1 – f_ck/250) = 0.6(1 – 35/250) = 0.516
f_cd = (α_cc ) f_ck)/γ_c = (1 × 35)/1.5 = 23.33 N/mm²
Let z = 0.9d
V_Rd,max = [(230 × 0.9 × 404 × 0.516 × 23.333)/(2.5 + 0.4)] × 10^-3 = 347.195 kN
Since V_Rd,c < V_Ed < V_Rd,max
Hence, A_sw/S = V_Ed/(0.87F_ykzcot θ) = 68330/(0.87 × 460 × 0.9 × 404 × 2.5) = 0.1878

Minimum shear reinforcement;
A_sw/S = ρ_w,min × b_w × sinα (α = 90° for vertical links)
ρ_w,min = (0.08 × √(F_ck))/F_yk = (0.08 × √35)/460 = 0.0010289
A_sw/S (min) = 0.0010289 × 230 × 1 = 0.2366
Since 0.2366 > 0.16809, adopt 0.2366
Maximum spacing of shear links = 0.75d = 0.75 × 404 = 303mm
Provide X8mm @ 275mm c/c (A_sw/S = 0.36556) Ok
The detailing sketches of the sections designed are shown below;

Loading, Analysis, and Design of Primary Beams

We can observe from the general arrangement of the structure that the primary beams are parallel to the short span direction of the slab. Therefore, the equivalent load that is transferred from the slab to the beam can be represented by;

p = nL_x/3 = (16.3425 × 3)/3 = 16.3425 kN/m

Since the beams are receiving loads from both sides, we can multiply by two (to account for the slab loads at the adjacent sides of the beam);

Hence p = 16.3425 × 2 = 32.685 kN/m

Self weight of the beam (ULS) = 1.35 × 0.9m × 0.4m × 25 kN/m³ = 12.15 kN/m
Therefore total uniformly distributed load on the primary beams = 32.685 + 12.15 = 44.835 kN/m

For beams on grid lines 2 and 5, the total load transferred from the secondary beams are the summation of the shear forces on supports 2 and 5 of the secondary beam. This is given by;

P = 104.78 kN + 91.11 kN = 195.89 kN

Structural Design
M_Ed = 1982.37 kNm
Effective depth (d) = h – C_nom – ϕ/2 – ϕ_links
Assuming ϕ32 mm bars will be employed for the main bars, and ϕ10mm bars for the stirrups (links)

d = 900 – 30 – 16 – 10 = 844 mm;

Effective flange width of the beam (T-beams)
b_eff = b_w + b’
Where b’ = 0.2(a_w + l_o) ≤ 0.4l_o ≤ 1.0a_w (for T-beams)
b_w = web width;
a_w = Clear distance between the webs of adjacent beams = 4000 – 315 = 3685 mm
l_o = The distance between points of zero moment on the beam (simply supported beam) = L = 12000 mm
Therefore in this case, b’ = 0.2(3685 + 12000) = 3137 mm ≤ 0.4l_o
Therefore b_eff = 400 + 3137 = 3537 mm
k = M_Ed/(f_ckb_wd²) = (1982.37 × 10⁶)/(35 × 3537 × 844²) = 0.0224
Since k < 0.167, no compression reinforcement required
z = d[0.5+ √(0.25 – 0.882K)] = z = d[0.5+ √(0.25 – 0.882(0.0224) ] = 0.95d
A_s1 = M_Ed/(0.87f_yk z) = (1982.37 × 10⁶)/(0.87 × 460 × 0.95 × 844) = 6177.91 mm²
Provide 8X32mm BOT (A_Sprov = 6432 mm²)

The minimum area of steel required;
f_ctm = 0.3 × f_ck^(2⁄3) = 0.3 × 35^(2⁄3) = 3.20996 N/mm² (Table 3.1 EC2)
AS_min = 0.26 × f_ctm/F_yk × b × d = 0.26 × 3.20996/460 × 400 × 844 = 612.458 mm²
Check if A_Smin < 0.0013 × b × d (438.88 mm₂)
Since, A_Smin = 612.458 mm², the provided reinforcement is adequate.

Shear Design
Support A
Ultimate shear force V_Ed = 562.84 kN

V_Rd,c = [C_Rd,c.k.(100ρ₁ f_ck)^(1/3) + k₁.σ_cp]b_w.d ≥ (V_min + k₁.σ_cp) b_w.d
Where;
C_Rd,c = 0.18/γ_c = 0.18/1.5 = 0.12
k = 1+√(200/d) = 1+√(200/844) = 1.486 > 2.0, therefore, k = 1.486 V_min = 0.035k^(3/2) f_ck^(1/2) = V_min = 0.035 × 1.486^(3/2) × 35^(1/2) = 0.375 N/mm₂
ρ₁ = As/bd = 3216/(400 × 844) = 0.009526 < 0.02; (Assuming only 4X32mm bars will be fully anchored at the supports. This is on the safer side for shear design)
σ_cp = 0

V_Rd,c = [0.12 × 1.486 (100 × 0.009526 × 35 )^(1/3)] 400 × 844 = 193759.0667 N = 193.759 kN
Since V_Rd,c (193.759 kN) < V_Ed (562.84 kN), shear reinforcement is required.

The compression capacity of the compression strut (V_Rd,max) assuming θ = 21.8° (cot θ = 2.5)
V_Rd,max = (b_w.z.v₁.f_cd)/(cot⁡θ + tanθ)
V₁ = 0.6(1 – f_ck/250) = 0.6(1 – 35/250) = 0.516
f_cd = (α_cc ) f_ck)/γ_c = (1 × 35)/1.5 = 23.33 N/mm²
Let z = 0.9d

V_Rd,max = [(400 × 0.9 × 844 × 0.516 × 19.8333)/(2.5 + 0.4)] × 10^-3 = 1072.239 KN
Since V_Rd,c < V_Ed < V_Rd,max
 
Hence, A_sw/S = V_Ed/(0.87F_ykzcot θ) = = 562840/(0.87 × 460 × 0.9 × 844 × 2.5 ) = 0.7405

Minimum shear reinforcement;
A_sw/S = ρ_w,min × b_w × sinα (α = 90° for vertical links)
ρ_w,min = (0.08 × √(F_ck))/F_yk = (0.08 × √35)/460 = 0.0010289

A_sw/S (min) = 0.0010289 × 400 × 1 = 0.41156
Since 0.7405 > 0.41156, adopt 0.7405
Maximum spacing of shear links = 0.75d = 0.75 × 844 = 633mm
Provide 2 Legs of X10mm @ 200mm c/c (A_sw/S = 0.785) Ok

Reinforcement Details of Primary Beams

According to clause 9.2.5 of EC2, where a beam is supported by a beam instead of a wall or column (primary and secondary beam interaction), reinforcement should be provided and designed to resist the mutual reaction. This reinforcement is in addition to that required for other reasons. The supporting reinforcement between two beams should consist of links surrounding the principal reinforcement of the supporting member. Some of these links may be distributed outside the volume of the concrete, which is common to the two beams.

In this case, additional links of X10@100mm c/c have been distributed at a length of 900mm on the primary beam, within the interaction zone (see detailing sketches below.

To download the full design paper in printable PDF format, click HERE.