Free Vibration of Trusses: A solved Example

Dynamics of structures is a special branch of structural analysis, which deals with the behaviour of structures subjected to dynamic loads (loads that vary with time). Such loads develop dynamic reactions, internal forces, and displacements in the structure. These values all change with time, and maximum values often exceed static load reaction values. Dynamic analysis of any structure often begins with free vibration analysis.

A structure undergoes free vibration when it is brought out of static equilibrium and can then oscillate without any external dynamic excitation. Free vibration of structures occurs with some frequencies which depend only on the parameters of the structures such as boundary conditions, distribution of masses, stiffnesses within the members etc, and not on the reason for the vibration.

At each natural frequency of free vibration, the structure vibrates in simple harmonic motion where the displaced shape (mode shape) of the structure is constant but the amplitude of the displacement varies in a sinusoidal manner with time. The number of natural frequencies in a structure coincides with the number of degrees of freedom in the structure. These frequencies are inherent to the given structure and are often referred to as eigenfrequencies. Each mode shape of vibration shows the form of an elastic curve which corresponds to a specific frequency.

Read also…
Deflection of trusses

Worked Example

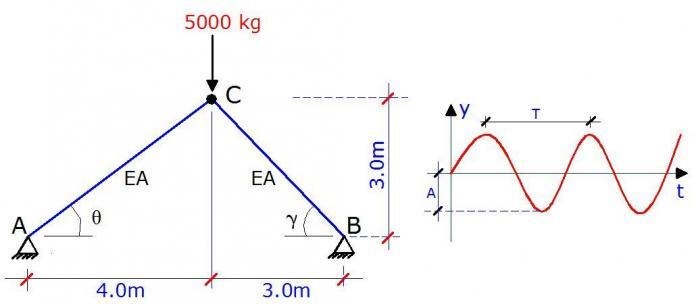
A truss is loaded as shown below with a lumped mass of 5000 kg. We are to obtain the eigenfrequencies and mode shapes by assuming linear behaviour, neglecting damping, and assuming that the stiffness and inertial effects are time-independent.

E = 205 kN/mm²
Cross-sectional area = 0.00548 m² (UB 254 x 146 x 43)

A little consideration will show that the structure has two degrees of freedom which are given by the vertical and horizontal translation at node C. The lumped mass at the node will definitely participate in those movements. The displacements are given by Y₁ and Y₂ below.

Geometrical Properties
θ = tan^-1(3/4) = 36.869°
cos θ = 0.8
sin θ = 0.6
L_AC = √(3² + 4²) = 5m

γ = tan^-1(4/4) = 45°
cos γ = 0.7071
sin γ = 0.7071
L_BC = √(3² + 3²) = 4.243m

ANALYSIS OF STATE 1; Y₁ = 1.0

∑F_y = 0
-0.6F_AC – 0.7071F_CB = 1.0 ———– (1)

∑F_x = 0
-0.8F_AC + 0.7071F_CB = 0 ———– (2)

Solving (1) and (2) simultaneously
F_AC = -0.7143
F_CB = -0.8081

ANALYSIS OF STATE 2; Y₂ = 1.0

∑F_y = 0
-0.6F_AC – 0.7071F_CB = 0 ———– (3)

∑F_x = 0
-0.8F_AC + 0.7071F_CB = -1.0 ———– (4)

Solving (3) and (4) simultaneously
F_AC = 0.7143
F_CB = -0.6061

The frequency equation of a 2 degree of freedom system in terms of displacement is given by;

Where;
M is the lumped mass
A is the amplitudes (Note that the system does not allow us to find the amplitudes but we can find the ratio of the amplitudes)
ω is the angular velocity
δ_ij is the axial displacement given by;

For the system above, we can easily compute this;

δ₁₁ = 1/EA[(-0.7143 × -0.7143 × 5) + (-0.8081 × -0.8081 × 4.243)] = 5.3219/EA
δ₂₂ = 1/EA[(0.7143 × 0.7143 × 5) + (-0.6061 × -0.6061 × 4.243)] = 4.1098/EA
δ₂₁ = δ₁₂ = 1/EA[(-0.7143 × 0.7143 × 5) + (-0.6011 × -0.8081 × 4.243)] = -0.4729/EA

To simplify our calculations, let δ₀ = 1/EA
Also let λ = 1/Mδ₀ω²

Therefore;

(5.3219 – λ)A₁ – 0.4729A₂ = 0
0.4729A₁ + (4.1098 – λ)A₂ = 0

On expanding;
λ² – 9.4317λ + 21.6484 = 0

On solving the quadratic equation;
λ₁ = 5.4845
λ₂ = 3.9472

You can verify that ω² = EA/λM

Therefore;
ω₁² = (0.1823 × 205 × 10⁶ × 0.00548)/5000 = 40.959
ω₂² = (0.2533 × 205 × 10⁶ × 0.00548)/5000 = 56.911

Hence;
ω₁ = 6.399 rad/s
ω₂ = 7.544 rad/s

To obtain the mode shapes;

For the first mode of vibration; Let A₁ = 1.0
(5.3219 – λ)A₁ – 0.4729A₂ = 0
(5.3219 – 5.4845) – 0.4729 A₂ = 0
Therefore, A₂ = -0.1626/0.4729 = -0.344
Φ₁ = [1.000 -0.344]^T

For the second mode of vibration; Let A₁ = 1.0
(5.3219 – λ)A₁ – 0.4729A₂ = 0
(5.3219 – 3.9472) – 0.4729 A₂ = 0
Therefore, A₂ = 1.3737/0.4729 = 2.9069
Φ₂ = [1.000 2.907]^T

The modal matrix is then defined as;

Remember Structville….
We have an interesting Facebook interactive page
Visit us at www.facebook.com/structville