Design of Precast Columns | Worked Example

Precast concrete columns are reinforced concrete columns that are cast and cured on the ground before being hoisted up and installed in their desired positions. Just like in-situ columns, precast columns are capable of resisting shear, axial force, and bending moment, however, careful attention must be paid to their connection details. The design of precast concrete columns involves the provision of adequate member size, reinforcement, and connection details to satisfy internal stresses due to externally applied loads, second-order effects, and lifting.

Different connection conditions can be adopted by different manufacturers. The foundation connection of a precast column may be achieved by allowing reinforcement bars to project from the column which is then passed through established sleeves before being filled with concrete grout. Alternatively, a base plate can be connected to the column which is then installed in position on a concrete base using bolts and nuts.

Precast columns may have corbels or nibs for supporting the beams. Alternatively, precast beam-column connections can be made using dowels or mechanical couplers.

Precast concrete columns have the following advantages over in-situ concrete construction;

1. Increased speed in construction since production of precast elements can commence ahead of time
2. Greater flexibility in project management and site planning due to off-site production capacity
3. Improved and higher quality of concrete, dimensions, and surface finishes
4. Reduction in site labour
5. Reduction in formwork requirement
6. Less wastage of materials

The design of precast reinforced concrete columns is carried out by a structural engineer and involves the following steps;

1. Confirm all dimensions and tolerances of the column and other members.
2. Analyse the structure to obtain the design bending moments, axial, and shear force
3. Check for column slenderness
4. Obtain the final design moments taking into account imperfections and second-order effects (if applicable)
5. Provide reinforcements to satisfy bending and axial force
6. Check for biaxial bending
7. Check for shear
8. Check that reinforcement provided satisfies bending and shear due to factory lifting
9. Check that reinforcement provided satisfies bending and shear due to site pitching
10. Design the connections
11. Detail the column as appropriate

Worked Example on the Design of Precast Columns | EN 1992-1:2004

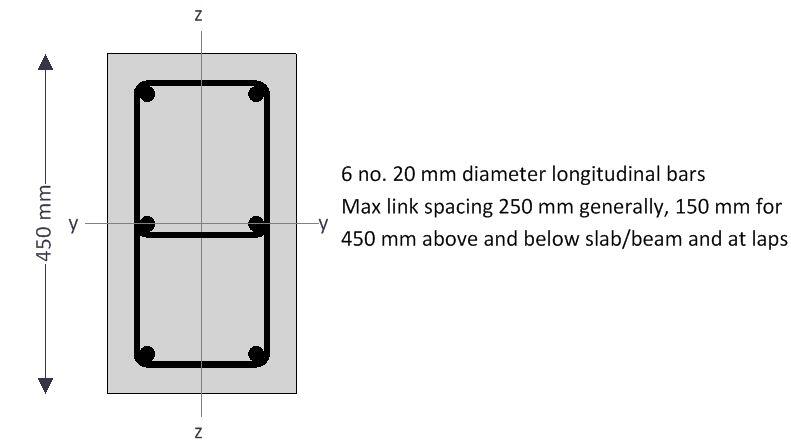
Check the capacity of a 4.5m high 450 x 250 mm precast column to resist the action effects given below. The column is reinforced with 6 numbers of H20 mm bars. f_ck = 35 N/mm²; f_yk = 500 N/mm²; Concrete cover = 35 mm. The design has been executed using Tekla Tedds software.

Axial load and bending moments from frame analysis
Design axial load;  N_Ed = 1350.0 kN
Moment about y-axis at top; M_top,y = 55.0 kNm
Moment about y-axis at bottom; M_btm,y = 22.0 kNm
Moment about z-axis at top; M_top,z = 11.4 kNm
Moment about z-axis at bottom; M_btm,z = 5.5 kNm

Column geometry
Overall depth (perpendicular to y-axis); h = 450 mm
Overall breadth (perpendicular to z-axis); b = 250; mm
Stability in the z-direction; Braced
Stability in the y-direction; Braced

Concrete details
Concrete strength class; C30/37
Partial safety factor for concrete (2.4.2.4(1)); γ_C = 1.50
Coefficient α_cc (3.1.6(1)); α_cc = 0.85
Maximum aggregate size; d_g = 20 mm

Reinforcement details
Nominal cover to links; c_nom = 35 mm
Longitudinal bar diameter; ϕ = 20 mm
Link diameter; ϕ_v = 8 mm
Total number of longitudinal bars; N = 6
No. of bars per face parallel to y-axis; N_y = 2
No. of bars per face parallel to z axis; N_z = ;3
Area of longitudinal reinforcement; A_s = N × π × ϕ² / 4 = 1885 mm²
Characteristic yield strength; f_yk = 500 N/mm²
Partial safety factor for reinft (2.4.2.4(1)); γ_S = 1.15
E_s = 200000 MPa

Column effective lengths
Effective length for buckling about y-axis; l_0y = 3500 mm
Effective length for buckling about z-axis; l_0z = 3900 mm

Effective depths of bars for bending about y-axis
Area per bar; A_bar = π × ϕ²/4 = 314 mm²
Spacing of bars in faces parallel to z-axis (centre to centre); 
s_z = h – 2 × (c_nom + ϕ_v) – ϕ)/ (N_z – 1) = 172 mm
Layer 1 (in tension face); d_y1 = h – c_nom – ϕ_v – ϕ/2 = 397 mm
Layer 2; d_y2 = d_y1 – s_z = 225 mm
Layer 3; d_y3 = d_y2 – s_z = 53 mm

2nd moment of area of reinforcement about y axis;                
I_sy = 2 × A_bar × [N_y × (d_y1 – h/2)²] = 3718 cm⁴
Radius of gyration of reinforcement about y-axis; i_sy = √(I_sy/A_s) = 140 mm
Effective depth about y axis (5.8.8.3(2)); d_y = h/2 + i_sy = 365 mm

Effective depths of bars for bending about z-axis
Area of per bar; A_bar = π × ϕ² / 4 = 314 mm²
Spacing of bars in faces parallel to y axis (c/c); s_y = (b – 2 × (c_nom + ϕ_v) – ϕ) / (N_y – 1) = 144 mm
Layer 1 (in tension face); d_z1 = b – c_nom – ϕ_v – ϕ/2 = 197 mm
Layer 2; d_z2 = d_z1 – s_y = 53 mm
Effective depth about z axis; d_z = d_z1 = 197 mm

Column slenderness about y-axis
Radius of gyration; i_y = h/√(12) = 13.0 cm
Slenderness ratio (5.8.3.2(1));  l_y = l_0y / i_y = 26.9

Column slenderness about z-axis
Radius of gyration; i_z = b/√(12) = 7.2 cm
Slenderness ratio (5.8.3.2(1));l_z = l_0z / i_z = 54.0

Design bending moments

Frame analysis moments about y axis combined with moments due to imperfections (cl. 5.2 & 6.1(4))
Eccentricity due to geometric imperfections (y axis); e_iy = l_0y /400 = 8.8 mm
Min end moment about y-axis; M_01y = min(|M_topy|, |M_btmy|) + e_iyN_Ed = 33.8 kNm
Max end moment about y-axis; M_02y = max(|M_topy|, |M_btmy|) + e_iyN_Ed = 66.8 kNm

Slenderness limit for buckling about y axis (cl. 5.8.3.1)
A = 0.7
Mechanical reinforcement ratio; ω = A_s × f_yd / (A_c × f_cd) = 0.429
Factor B; B = √(1 + 2ω) = 1.363
Moment ratio; r_my = M_01y / M_02y = 0.506
Factor C; C_y = 1.7 – r_my = 1.194
Relative normal force; n = N_Ed / (A_c × f_cd) = 0.706
Slenderness limit;  l_limy = 20 × A × B × C_y / √(n) = 27.1

l_y < l_limy – Second order effects may be ignored

Frame analysis moments about z-axis combined with moments due to imperfections (cl. 5.2 & 6.1(4))
Ecc. due to geometric imperfections (z axis); e_iz = l_0z /400 = 9.8 mm
Min end moment about z axis; M_01,z = min(|M_topz|, |M_btmz|) + e_izN_Ed = 18.7 kNm
Max end moment about z axis; M_02,z = max(|M_topz|, |M_btmz|) + e_izN_Ed = 24.5 kNm

Slenderness limit for buckling about y-axis (cl. 5.8.3.1)
A = 0.7
Mechanical reinforcement ratio; w = A_s × f_yd / (A_c × f_cd) = 0.429
Factor B; B = √(1 + 2ω) = 1.363
Moment ratio; r_mz = 1.000
Factor C;  C_z = 1.7 – r_mz = 0.700
Relative normal force; n = N_Ed / (A_c × f_cd) = 0.706
Slenderness limit;  l_limz = 20 × A × B × C_z / √(n) = 15.9
l_z > l_limz – Second order effects must be considered

Design bending moments (cl. 6.1(4))
Design moment about y axis;   M_Edy = max(M_02y, N_Ed × max(h/30, 20 mm)) = 66.8 kNm

Local second order bending moment about z-axis (cl. 5.8.8.2 & 5.8.8.3)
Relative humidity of ambient environment; RH = 50 %
Column perimeter in contact with atmosphere; u = 1400 mm
Age of concrete at loading;  t₀ = 28 day
Parameter n_u; n_u = 1 + w = 1.429
n_bal = 0.4
Approx value of n at max moment of resistance;  n_bal = 0.4
Axial load correction factor; K_r = min(1.0 , (n_u – n) / (n_u – n_bal)) = 0.703
Reinforcement design strain; ε_yd = f_yd/E_s = 0.00217

Basic curvature; curve_{basic_z} = ε_yd / (0.45 × d_z) = 0.0000245 mm^-1

Notional size of column; h₀ = 2 × A_c / u = 161 mm
Factor a₁ (Annex B.1(1));   a₁ = (35 MPa / f_cm)^0.7 = 0.944
Factor a₂ (Annex B.1(1)); a₂ = (35 MPa / f_cm)^0.2 = 0.984

Relative humidity factor (Annex B.1(1));
ϕ_RH = [1 + ((1 – RH/100%) / (0.1 mm^-1/3 × (h₀)^1/3)) × a₁] × a₂ = 1.838

Concrete strength factor (Annex B.1(1));
β_fcm = 16.8 × (1 MPa)^1/2 / √(f_cm) = 2.725

Concrete age factor (Annex B.1(1));                           
β_t0 = 1 / (0.1 + (t₀ / 1 day)^0.2) = 0.488

Notional creep coefficient (Annex B.1(1));                 
ϕ₀ = ϕ_RH × β_fcm × β_t0 = 2.446

Final creep development factor; (at t = ∞); β_c∞ = 1.0
Final creep coefficient (Annex B.1(1));ϕ_∞ = ϕ₀ × β_c∞ = 2.446

Ratio of SLS to ULS moments r_Mz (say) = 0.80

Effective creep ratio (5.8.4(2));  f_efz = f_∞ × r_Mz = 1.957

Factor β; β_z = 0.35 + f_ck / 200 MPa – l_z / 150 = 0.140
Creep factor;  K_ϕz = max(1.0, 1 + β_z × ϕ_efz) = 1.273
Modified curvature;  curve_{mod_z} = K_r × K_ϕz × curve_{basic_z} = 0.0000219 mm^-1
Curvature distribution factor; c = 10

Deflection; e_2z = curve_{mod_z} × l_0z²/c = 33.4 mm

Nominal 2^nd order moment;                                          
M_2z = N_Ed × e_2z = 45.1 kNm

Design bending moment about z-axis (cl. 5.8.8.2 & 6.1(4))
Equivalent moment from frame analysis;                 
M_0ez = max(0.6 × M_02z + 0.4 × M_01z, 0.4 × M_02z) = 22.2 kNm

Design moment;
M_Edz = max(M_02z, M_0ez + M_2z, M_01z + 0.5 × M_2z, N_Ed × max(b/30, 20 mm))
M_Edz = 67.2 kNm

Moment capacity about y-axis with axial load (1350.0 kN)
Moment of resistance of concrete
By iteration:
Position of neutral axis; y = 317.8 mm

Concrete compression force (3.1.7(3));                     
F_yc = h × f_cd × min(l_sb × y, h) × b = 1080.6 kN

Moment of resistance;                                                   
M_Rdyc = F_yc × [h / 2 – (min(l_sb × y, h)) / 2] = 105.8 kNm

Moment of resistance of reinforcement
Strain in layer 1; ε_y1 = ε_cu3 × (1 – d_y1/y) = -0.00087
Stress in layer 1; σ_y1 = max(-1 × f_yd, E_s × ε_y1) = -174.4 N/mm²
Force in layer 1; F_y1 = N_y × A_bar × σ_y1 = -109.6 kN
Moment of resistance of layer 1; M_Rdy1 = F_y1 × (h/2 – d_y1) = 18.8 kNm

Strain in layer 2; ε_y2 = ε_cu3 × (1 – d_y2 / y) = 0.00102
Stress in layer 2; σ_y2 = min(f_yd, E_s × ε_y2) – h × f_cd = 187.4 N/mm²
Force in layer 2; F_y2 = 2 × A_bar × σ_y2 = 117.8 kN
Moment of resistance of layer 2; M_Rdy2 = F_y2 × (h/2 – d_y2) = 0.0 kNm

Strain in layer 3; ε_y3 = ε_cu3 × (1 – d_y3/y) = 0.00292
Stress in layer 3; σ_y3 = min(f_yd, E_s × ε_y3) – h × f_cd = 417.8 N/mm²
Force in layer 3; F_y3 = N_y × A_bar × σ_y3 = 262.5 kN
Moment of resistance of layer 3; M_Rdy3 = F_y3 × (h/2 – d_y3) = 45.2 kNm

Resultant concrete/steel force; F_y = 1351.2 kN
PASS – This is within half of one percent of the applied axial load

Combined moment of resistance
Moment of resistance about y axis; M_Rdy = 169.8 kNm
PASS – The moment capacity about the y axis exceeds the design bending moment

Moment capacity about z-axis with axial load (1350.0 kN)

Moment of resistance of concrete
By iteration, position of neutral axis; z = 171.9 mm
Concrete compression force (3.1.7(3)); F_zc = h × f_cd × min(l_sb × z, b) × h = 1051.9 kN
Moment of resistance; M_Rdzc = F_zc × [b / 2 – (min(l_sb × z, b)) / 2] = 59.2 kNm

Moment of resistance of reinforcement
Strain in layer 1; ε_z1 = ε_cu3 × (1 – d_z1 / z) = -0.00051
Stress in layer 1; σ_z1 = max(-1 × f_yd, E_s × ε_z1) = -102.3 N/mm²
Force in layer 1; F_z1 = N_z × A_bar × σ_z1 = -96.4 kN
Moment of resistance of layer 1; M_Rdz1 = F_z1 × (b / 2 – d_z1) = 6.9 kNm

Strain in layer 2; ε_z2 = ε_cu3 × (1 – d_z2/z) = 0.00242
Stress in layer 2; σ_z2 = min(f_yd, E_s × ε_z2) – h × f_cd = 417.8 N/mm²
Force in layer 2; F_z2 = N_z × A_bar × σ_z2 = 393.8 kN
Moment of resistance of layer 2; M_Rdz2 = F_z2 × (b/2 – d_z2) = 28.4 kNm

Resultant concrete/steel force; F_z = 1349.2 kN
PASS – This is within half of one percent of the applied axial load

Combined moment of resistance
Moment of resistance about z-axis; M_Rdz = 94.5 kNm
PASS – The moment capacity about the z-axis exceeds the design bending moment

Biaxial bending

Determine if a biaxial bending check is required (5.8.9(3))

Ratio of column slenderness ratios; ratio_l = max(l_y, l_z) / min(l_y, l_z) = 2.01
Eccentricity in direction of y axis; e_y = M_Edz/N_Ed = 49.8 mm
Eccentricity in direction of z axis; e_z = M_Edy/N_Ed = 49.5 mm

Equivalent depth; h_eq = i_y × √(12) = 450 mm
Equivalent width; b_eq = i_z × √(12) = 250 mm

Relative eccentricity in direction of y-axis; e_{rel_y} = e_y/b_eq = 0.199
Relative eccentricity in direction of z-axis; e_{rel_z} = e_z/h_eq = 0.110

Ratio of relative eccentricities;                                      
ratio_e = min(e_{rel_y}, e_{rel_z})/max(e_{rel_y}, e_{rel_z}) = 0.552

ratio_l > 2 and ratio_e > 0.2
Therefore, biaxial bending check is required.

Biaxial bending (5.8.9(4))
Design axial resistance of section; N_Rd = (A_c × f_cd) + (A_s × f_yd) = 2732.0 kN
Ratio of applied to resistance axial loads; ratio_N = N_Ed / N_Rd = 0.494
Exponent a; a = 1.33

Biaxial bending utilisation; UF = (M_Edy/M_Rdy)^a + (M_Edz/M_Rdz)^a = 0.926 (Okay)

Shear

Design shear force; V_Ed = V_Ed,y = 25.8 kN
C_Rd,c = 0.18/γ_C = 0.12
Tension reinforcement; A_sl = N_z × π × ϕ²/4 = 942 mm²
Depth of tension reinforcement; d_v = d_z1 = 197 mm
k_shear = min(1 + (200 mm / d_v)^0.5, 2) = 2.000
Width of the cross section in tensile area; b_w = h = 450 mm
Longitudinal reinforcement ratio; r_l = min(A_sl/(b_w × d_v), 0.02) = 0.01063

Axial pressure in cross-section; σ_cp = min(N_Ed/A_c, 0.2 × f_cd) = 3.40 N/mm²
v_min = 0.035 N^0.5/mm × k_shear^3/2 × f_ck^1/2 = 0.54 N/mm²
k_1,shear = 0.15

Design shear resistance – exp. 6.2 a & b;                 
V_Rd,c = max(C_Rd,c × k_shear × (100 N²/mm⁴ × r_l × f_ck)^1/3, v_min) × b_w × d_v + k_1,shear × σ_cp × b_w × d_v = 112.7 kN
V_Ed / V_Rd,c = 0.23
PASS – Design shear resistance exceeds design shear force

Factory Lifting Check

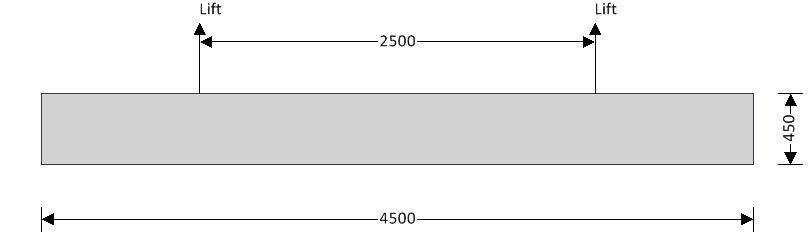
Precast element details
Total length of column;  L_element = 4500 mm
Distance between lifting points; L_lift = 2500 mm
Lifting load coefficient; f_lifting = 1.50
Permanent load factor; γ_G = 1.35
Formwork adhesion force; q_formwork = 2.0 kN/m²
Self weight of precast element; w_{self_precast} = b × h × ρ_conc × g_acc + q_formwork × b = 3.3 kN/m

Lifting check (positive moment)
Design bending moment; M = γ_G × f_lifting × (w_{self_precast} × L_lift² /8 – w_{self_precast} × ((L_element – L_lift) / 2)²/2) = 1.9 kNm

Effective depth of tension reinforcement; d = 397 mm
Redistribution ratio; d = 1.000
K = M / (b × d² × f_ck) = 0.002
No compression reinforcement is required

Lever arm; z = min(0.5 × d × (1 + (1 – 2 × K / (h × a_cc / γ_C))^0.5), 0.95 × d) = 377 mm
Depth of neutral axis; x = 2 × (d – z)/l_sb = 50 mm

Area of tension reinforcement required; A_s,pos = M / (f_yd × z) = 11 mm²
Tension reinforcement provided; 2H20 mm (A_s,prov = 628 mm²)
Minimum area of reinforcement – exp.9.1N; A_s,min = max(0.26 × f_ctm/f_yk, 0.0013) × b × d = 149 mm²
Maximum area of reinforcement – cl.9.2.1(3); A_s,max = 0.04 × b × h = 4500 mm²
Required area of reinforcement; A_s,req = 149 mm²
A_s,req / A_s,prov = 0.24 (okay)

Lifting check (negative moment)
Design bending moment; M = γ_G × f_lifting × w_{self_precast} × ((L_element – L_lift) / 2)² / 2 = 3.3 kNm
Effective depth of tension reinforcement; d = 397 mm
Redistribution ratio; d = 1.000
K = M / (b × d² × f_ck) = 0.003

Area of tension reinforcement required; A_s,neg = M / (f_yd × z) = 20 mm²
Tension reinforcement provided; 2H20 mm (A_s,prov = 628 mm²)
Minimum area of reinforcement – exp.9.1N; A_s,min = max(0.26 × f_ctm/f_yk, 0.0013) × b × d = 149 mm²
Maximum area of reinforcement – cl.9.2.1(3); A_s,max = 0.04 × b × h = 4500 mm²
Required area of reinforcement; A_s,req = 149 mm²
A_s,req / A_s,prov = 0.24 (Okay)

Lifting check (Shear)
Design shear force at critical shear plane;
V_Ed = γ_G × f_lifting × w_{self_precast} × max(L_lift / 2, (L_element – L_lift) / 2) = 8.2 kN

C_Rd,c = 0.18/γ_C = 0.12

Tension reinforcement; A_sl = N_y × π × ϕ² / 4 = 628 mm²
Depth of tension reinforcement; d_v = d_y1 = 397 mm
k_shear = min(1 + (200 mm / d_v)^0.5, 2) = 1.710

Width of the cross section in tensile area; b_w = b = 250 mm

Longitudinal reinforcement ratio; ρ_l = min(A_sl / (b_w × d_v), 0.02) = 0.00633
v_min = 0.035 N^0.5/mm × k_shear^3/2 × f_ck^1/2 = 0.43 N/mm²

Design shear resistance – exp. 6.2 a & b;                 
V_Rd,c = max(C_Rd,c × k_shear × (100 N²/mm⁴ × ρ_l × f_ck)^1/3, v_min) × b_w × d_v
V_Rd,c = 54.3 kN
V_Ed / V_Rd,c = 0.15 (This is okay)

On-site Pitching Check

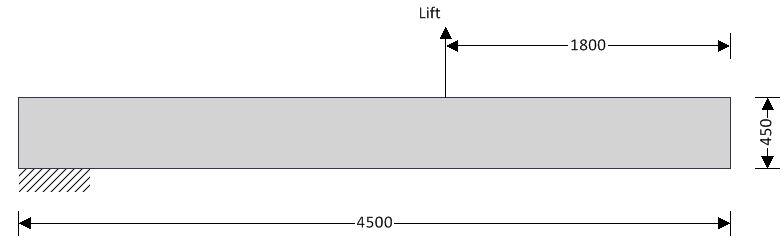
Precast element details
Total length of column; L_element = 4500 mm
Distance to the pitching point; L_pitch = 1800 mm
Distance from pitching point to end of column;L_end = 2700 mm
Lifting load coefficient; f_pitching = 1.25
Permanent load factor; g_G = 1.35
Self weight of precast element; w_{self_precast} = b × h × ρ_conc × g_acc = 2.8 kN/m

Lifting check (positive moment)
Design bending moment (at 3750 mm);
M = g_G × f_pitching × w_{self_precast} × L_element² / (2 × L_end) × (0.25 × L_element²/L_end – L_pitch) = 1.3 kNm

Effective depth of tension reinforcement; d = 397 mm
Redistribution ratio; d = 1.000
K = M / (b × d² × f_ck) = 0.001

Area of tension reinforcement required; A_s,pos = M / (f_yd × z) = 8 mm²
Tension reinforcement provided; 2H20 mm (A_s,prov = 628 mm²)
Minimum area of reinforcement – exp.9.1N; A_s,min = max(0.26 × f_ctm/f_yk, 0.0013) × b × d = 149 mm²
Maximum area of reinforcement – cl.9.2.1(3); A_s,max = 0.04 × b × h = 4500 mm²
Required area of reinforcement; A_s,req = 149 mm²
A_s,req / A_s,prov = 0.24 (Okay)

Lifting check (negative moment)
Design bending moment; M = g_G × f_pitching × w_{self_precast} × L_pitch ² / 2 = 7.5 kNm
Effective depth of tension reinforcement; d = 397 mm
Redistribution ratio; d = 1.000

K = M / (b × d² × f_ck) = 0.006

Area of tension reinforcement required; A_s,neg = M / (f_yd × z) = 46 mm²

Tension reinforcement provided; 2H20 mm (A_s,prov = 628 mm²)
Minimum area of reinforcement – exp.9.1N; A_s,min = max(0.26 × f_ctm/f_yk, 0.0013) × b × d = 149 mm²
Maximum area of reinforcement – cl.9.2.1(3); A_s,max = 0.04 × b × h = 4500 mm²
Required area of reinforcement; A_s,req = 149 mm²
A_s,req / A_s,prov = 0.24 (Okay)

Lifting check (Shear)
Design shear force at critical shear plane;             
V_Ed = g_G × f_pitching × w_{self_precast} × max(L_pitch, abs(L_element – 0.5 × L_element² / L_end), abs(L_end – (L_element – 0.5 × L_element² / L_end))) = 9.1 kN

C_Rd,c = 0.18/γ_C = 0.12
Tension reinforcement; A_sl = N_y × π × ϕ² / 4 = 628 mm²
Depth of tension reinforcement; d_v = d_y1 = 397 mm
k_shear = min(1 + (200 mm / d_v)^0.5, 2) = 1.710

Width of the cross section in tensile area; b_w = b = 250 mm

Longitudinal reinforcement ratio; ρ_l = min(A_sl / (b_w × d_v), 0.02) = 0.00633
v_min = 0.035 N^0.5/mm × k_shear^3/2 × f_ck^1/2 = 0.43 N/mm²

Design shear resistance – exp. 6.2 a & b;                 
V_Rd,c = max(C_Rd,c × k_shear × (100 N²/mm⁴ × ρ_l × f_ck)^1/3, v_min) × b_w × d_v
V_Rd,c = 54.3 kN
V_Ed / V_Rd,c = 0.17 (Okay)

Connection

The connection of the column can be designed and checked depending on the method adopted.