The stress in the soil mass is affected by the previous loading history. When a new foundation is constructed, the new load can either increase or decrease the existing stresses in the soil. The response of the soil mass to the new load depends on the previous stress history. Therefore, it is important to understand the stress imprint of the soil mass before designing a foundation.
The term “stress imprint” refers to the state of stresses that are locked into the soil structure. These stresses are locked in because the soil particles have rearranged and formed bonds. The bonds prevent the stresses from being released, even when the load is removed. The stress imprint can be either positive or negative.
A positive stress imprint is created when the soil is loaded to a higher stress than it is currently experiencing (normally consolidated soil). A negative stress imprint is created when the soil is unloaded to a lower stress than it is currently experiencing (overconsolidated soil).
The stress imprint can affect the behaviour of the soil in a number of ways. For example, a positive stress imprint can make the soil more resistant to shearing, while a negative stress imprint can make the soil more susceptible to settlement.
The stress imprint can be difficult to measure, but there are a number of techniques that can be used. One common technique is to use a pressuremeter. A pressuremeter is a device that is inserted into the soil and used to measure the stresses in the soil.
In-Situ Stresses in Soil
In situ, the vertical stresses act on a horizontal plane at some depth z. These can be computed in any general case as the sum of contributions from n strata of unit weight γi and thickness zi as;
po = ∑γizi —— (1)
In the context of the formation of soil deposits, the area of the land where soil accumulates is typically extensive, and the depth of the deposit keeps increasing until either the accumulation process or the internal weathering process halts. This transition leads to a gradual downward compression of the soil at any specific depth.
Likewise, the vertical stress also increases due to this compression, and in almost all instances, the unit weight of the soil is a function of depth. Given the substantial lateral extent of the deposit, there is limited justification for notable lateral compression to take place.
Consequently, it is reasonable to anticipate that the vertical locked-in effective stresses (p’o) would surpass the effective lateral stresses (σ’h) at the same location. This relationship between horizontal and vertical stresses can be defined as the ratio of the two.
K = σh/po ——– (2)
which is valid for any depth z at any time.
K0 Conditions
Over geological time the stresses in a soil mass at a particular level stabilize into a steady state and strains become zero. When this occurs the vertical and lateral stresses become principal stresses acting on principal planes. This effective stress state is termed the at-rest or K0 condition with K0 defined as;
K0 = σ’h/p’o ——– (3)
Therefore, Ko conditions refer to the state of stresses in a soil mass when there is no lateral strain. This means that the soil is not allowed to deform horizontally. Ko conditions are typically found in undisturbed soil, where the soil has not been subjected to any significant lateral stresses.
Figure 2 shows the range of K0 and the relationship between po and σh in any homogeneous soil. The figure also shows the qualitative curves for preconsolidation in the upper zone of some soil from shrinkage/chemical effects. The figure clearly illustrates the anisotropic (σv ≠ σh) stress state in a soil mass.
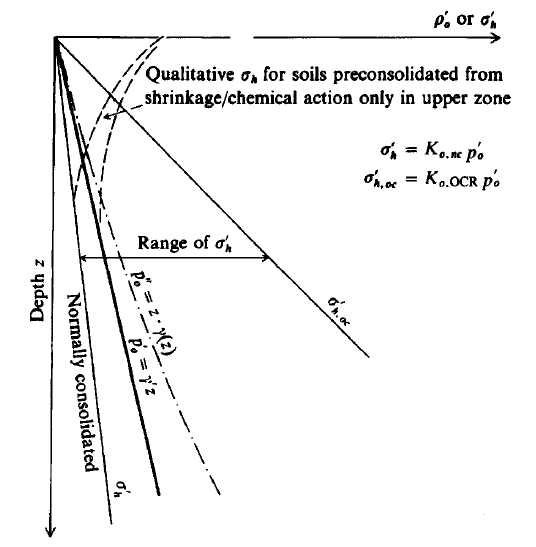
In the figure above, although the linear vertical (also called geostatic) pressure profile is commonly used, the p’0 effective pressure profile is more realistic of real soils since γ usually increases with depth. The lateral pressure profile range is for the geostatic pressure profile and would be curved similarly to the p’o curve for real soils.
K₀ conditions are critical for:
- Retaining wall design.
- Excavation support.
- Earthquake-induced lateral pressures.
- Soil-structure interaction.
Because of the sampling limitations, it is an extremely difficult task to measure K0 either in the laboratory or in situ. Some field methods are available, but note that they are very costly for the slight improvement—in most cases—over using one of the simple estimates following. In these equations use the effective angle of internal friction ‘ and not the total stress value.
Jaky (1948) presented a derived equation for K0 that is applicable to both soil and agricultural grains (such as corn, wheat, oats, etc.) as;
K0 = [(1 – sinφ’)/(1 + sinφ’)] × ( 1 + 2/3sinφ’) ——– (4)
which has been simplified—and erroneously called “Jaky’s equation”— to the following:
K0 = 1 – sinφ’ ——— (5)
This equation is very widely used and has proved reasonably reliable in comparing initial to back-computed K0 values in a number of cases and for normally consolidated materials. Kezdi (1972) suggests that for sloping ground Jaky’s equation can be used as follows:
K0 = (1 – sinφ’)/(1 + sinβ) ——– (6)
where β is the angle with the horizontal (with sign) so that K0 is either increased or reduced as site conditions dictate. This reference also gives a partial derivation of the Jaky equation for any interested user.
Brooker and Ireland (1965) (for normally consolidated clay) suggest;
K0 = 0.95 – sinφ’ ——– (7)
Alpan (1967) (for normally consolidated clay) suggests;
K0 = 0.19 + 0.233 log10 Ip ——– (8)
An equation similar to Eq. (8) is given by Holtz and Kovacs (1981) as;
K0 = 0.44 + 0.0042Ip ——– (9)
where Ip is the plasticity index of the soil in percent.
We can readily derive a value for K0 in terms of Poisson’s ratio based on the definition of K0 being an effective stress state at zero strain. From Hooke’s law, the lateral strain in terms of the effective horizontal (x, z) and vertical (y) stresses is;
εx = 0 = 1/Es(σx – μσy – μσz) = εz ——– (10)
For a cohesionless, soil μ is often assumed as 0.3 to 0.4, which gives K0 = 0.43 to 0.67, with a value of 0.5 often used. It is extremely difficult to obtain a reliable estimate of K0 in a normally consolidated soil, and even more so in overconsolidated soils (OCR > 1). A number of empirical equations based on various correlations have been given in the literature. Several of the more promising ones are:
Alpan (1967) and others have suggested that the overconsolidated consolidation ratio K0,OCR is related to the normally consolidated value K0,nc in the following form;
K0,OCR = K0,nc × OCRn (2-23) ——– (11)
where n = f(test, soil, locale) with a value range from about 0.25 to 1.25. For overconsolidated sand, n can be estimated from Figure 3.
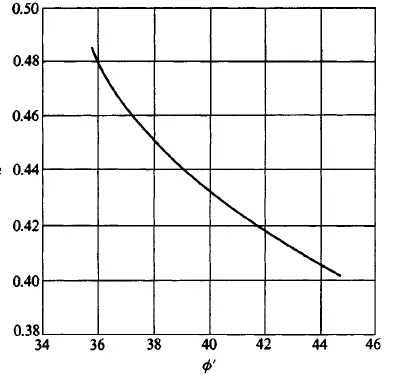
For cohesive soil, Wroth and Houlsby (1985) suggest n as follows:
n = 0.42 (low plasticity — IP < 40%)
n = 0.32 (high plasticity — IP > 40%)
However, n ≈ 0.95 to 0.98 was obtained from in situ tests on several clays in eastern Canada. Mayne and Kulhawy (1982) suggest that a mean value of n = 0.5 is applicable for both sands and clays and that n = sinφ’ is also a good representation for sand. Their suggestions are based on a semi-statistical analysis of a very large number of soils reported in the
literature.
The exponent n for clays was also given by Alpan (1967) in graph format and uses the plasticity index IP (in percent). The author modified the equation shown on that graph to obtain;
n = 0.54 × 10(-IP/281) ——– (12)
And, as previously suggested (for sands), we can use;
n = sinφ’ ——— (13)
Conclusion
Geostatic conditions refer to the stress state within a soil mass due to the weight of the overlying soil. These stresses are primarily vertical and compressive, but they also induce horizontal stresses due to the frictional resistance of the soil particles. The magnitude of these stresses depends on the depth of the soil layer, the unit weight of the soil, and the geometry of the soil mass.
The K0 condition, also known as the at-rest earth pressure, represents a specific stress state within a soil mass where there is no lateral strain. This condition occurs when the soil is horizontally constrained, such as by a retaining wall or a layer of bedrock. In K0 conditions, the horizontal effective stress (σ’h) is typically about 0.5 to 0.7 times the vertical effective stress (σ’v). The factors affecting K0 values are the overconsolidation ratio, type of soil, confining pressure, stress history, and effective stress state.










