Design of Pile Foundation System for Bridge Piers

Piles are the most preferred type of foundation for supporting the piers of overhead bridges. They offer greater resistance to vertical and horizontal actions from the bridge deck than shallow foundations. Furthermore, they extend the foundation of piers beyond scouring zones so that there will be no loss of bearing capacity. In this article, we are going to show how to design the foundation of a bridge pier using piles.

We have previously talked about the design the piers and pier cap of an overhead bridge. If you missed the post, read it below.

Structural Design of Pier and Pier Caps of Highway Bridges

Let us go ahead and design the foundation of the bridge pier using the soil investigation report shown below.

Step 1: Determine the load from the superstructure

The loading on the pier cap at ultimate limit state and serviceability limit state are shown below;

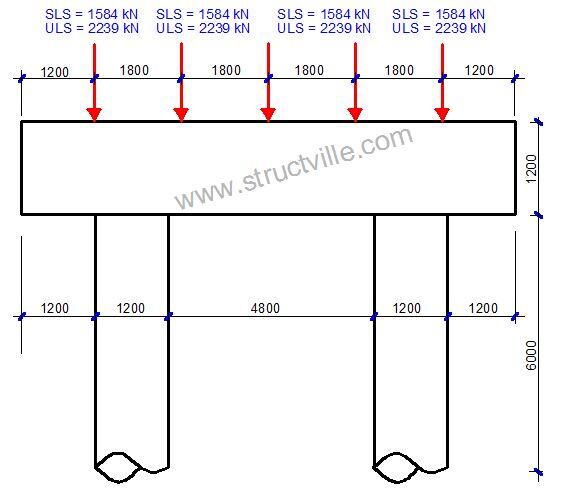
When analysed on Staad Pro, the following support reactions were obtained;

ULS
Vertical support reaction on each pier = 6001.483 kN
Horizontal reaction = 368.443 kN
Bending Moment = 702.032 kNm

SLS
Vertical support reaction on each pier = 4259.247 kN
Horizontal reaction = 260.901 kN
Bending Moment = 497.125 kNm

Step 2: Determination of the number of piles required and the layout

We normally use the service loads to determine the number of piles required for the structure, and use ultimate loads (factored loads) for the structural design.

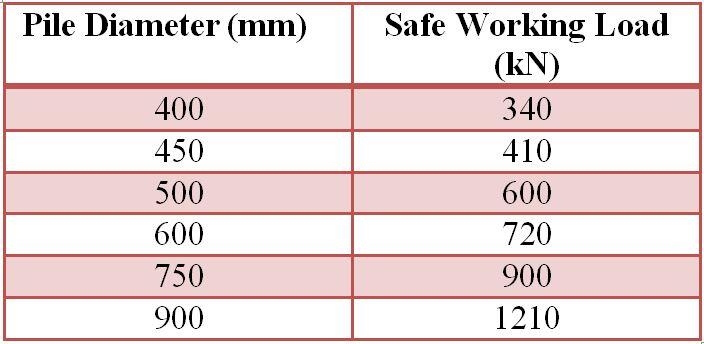
Using 900 diameter piles, Number of piles required per pier = 4259.247/1210 = 3.52
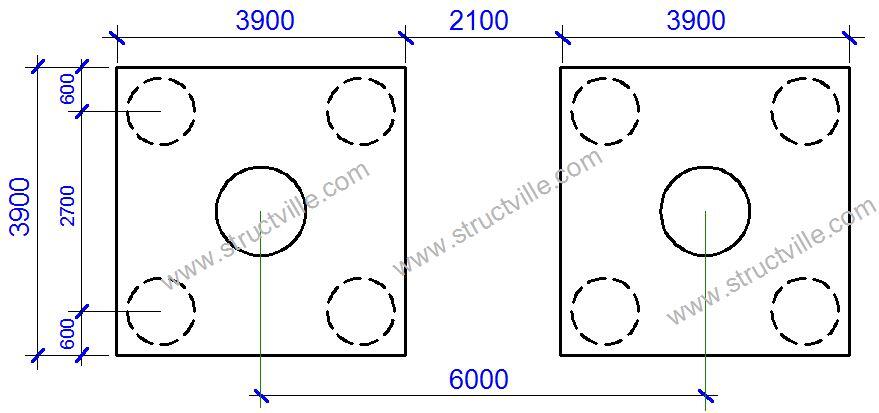
Therefore, provide 4 Piles per pier leg. The layout of the pile cap is shown below. However, attempts were made to combine the two piers under one pile cap, but no economical solution was reached due to the wide spacing of the piers (6 m).

Step 3: Provide longitudinal reinforcement for the piles

The reinforcements required for the piles is usually based on the minimum required for the selected pile diameter

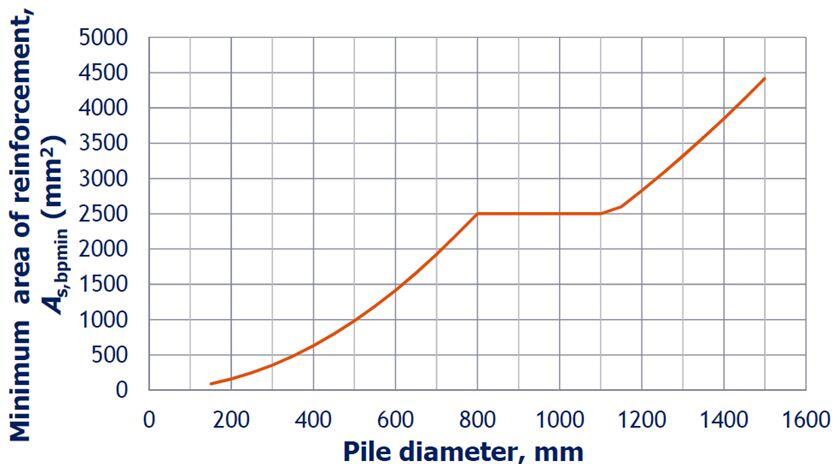
For a pile diameter of 900 mm, the minimum area of steel required is 2500 mm²
Therefore provide 9H20 mm (A_sprov = 2826 mm²)
Provide helical links of H10@250 pitch

Read also…
Reinforcement design of piles

Step 4: Analyse and design the pile cap

The required thickness of the pile cap is usually estimated from the diameter of the piles.

h = 2 x diameter of piles + 100 = 2(900) + 100 = 1900 mm deep pile cap

Different approaches can be used for analysing the pile cap such as bending theory, strut and tie method, or finite element analysis. Let us obtain the internal forces in the pile cap from finite element analysis using Staad Pro.

When analysed at ULS, the maximum moment in the pile cap is shown below;

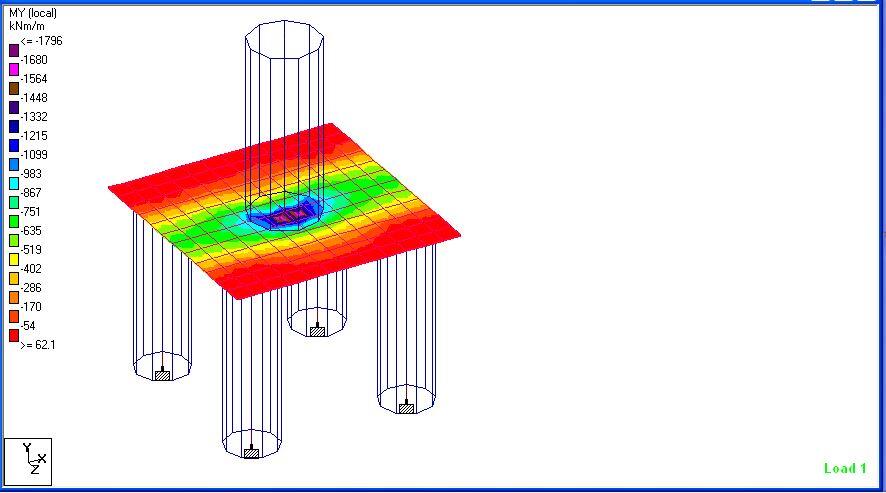
M_Ed = 1796 KN.m/m

Effective depth d = 1900 – 100  = 1800 mm

k = M_Ed/(f_ckbd²) = (1796 × 10⁶)/(40× 1000 × 1800²) = 0.0138

Since k < 0.167, no compression reinforcement required
z = d[0.5+ √(0.25 – 0.882k)]
z = d[0.5+ √(0.25 – 0.882(0.0138))] = 0.95d

A_s1 = M_Ed/(0.87_yk z) = (1796 × 10⁶)/(0.87 × 500 × 0.95 × 1800) = 2414 mm²/m
Provide 20H25mm BOT (AS_prov = 8380 mm²)

If we are to use simplified strut and tie method;

F_t = (N_Ed x l)/8d = (6001.483 x 2.7)/(8 x 1.8) = 1125.28 kN
A_st = F_t/0.87f_yk = (1125.28 x 10³)/(0.87 x 500) = 2587 mm²/m

You can compare the two results above.

To calculate the minimum area of steel required;

A_Smin = 0.26 (f_ctm/f_yk)bd
f_ctm = 0.3f_ck^2/3 = 0.3 x 40^(2/3) = 3.51 N/mm²
A_Smin = 0.26 x (3.51/500) x 1000 x 1800 = 3285 mm²/m

Check if  A_Smin < 0.13bd/100 = 2340 mm²/m

Provide H32 @ 225 c/c (As_prov = 3573 mm²)

Read also…
Structural aspects of pile foundation design

Step 5: Check for punching shear around the pier perimeter

V_Ed = 6001.483 kN

Column perimeter u = πd = π x 1200 = 3769.9 mm

v = V/ud
v = (6001.483 × 1000)/(3769.9 × 1800) = 0.8844 N/mm²
V_Rd,max = 0.2(1 –  f_ck/250)f_cd
V_Rd,max = 0.2 (1 – 40/250) x 40/1.5 = 4.48 N/mm²

0.8844 N/mm² > 4.48 N/mm² This is okay

This shows that the punching shear around column perimeter is ok.

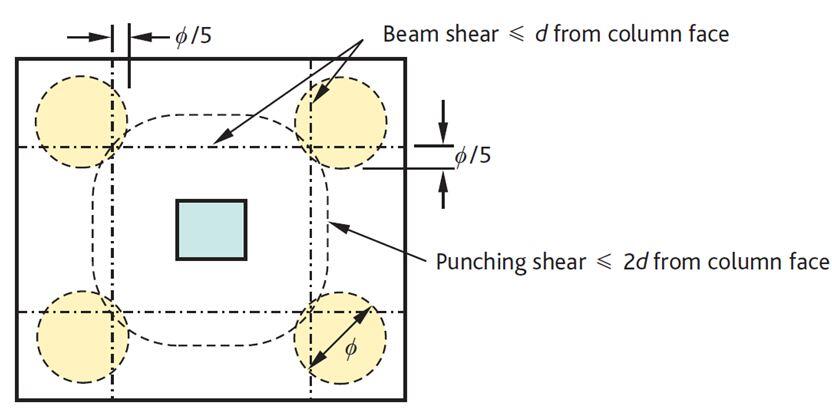
Step 6: Check for critical punching shear

Consider the critical section for shear to be located at 20% of the pile diameter inside the pile cap.

Distance of this section from the column face;
a_v = 0.5(Spacing between piles – width of column) – 0.3(pile diameter)
a_v = 0.5(2700 – 1200) – 0.3(900) = 480 mm

Length of corresponding perimeter for punching shear
u = 4(2160) = 8640 mm

Perimeter of pile cap = 4(3900) = 15600 mm

The contribution of the column load to the shear force may be reduced by applying a factor β = a_v/2d, since a_v < 2d where 0.5d ≤ a_v ≤ 2d

But a little consideration will show that a_v(480 mm) < 0.5d(900 mm), therefore, take a_v as 0.5d (900)
Therefore β = 900/2(1800) = 0.25

v = βV/bd
V = 6001.483/4 = 1500.37 kN

v = (0.25 x 1500.37 x 10³)/(1000 x 1800) = 0.208 N/mm²

V_Rd,c = [C_Rd,c.k.(100ρ₁ f_ck)^(1/3)]

Where;
C_Rd,c = 0.18/γ_c = 0.18/1.5 = 0.12
k = 1 + √(200/d) = 1 + √(200/1800) = 1.33 > 2.0, therefore, k = 1.33
ρ₁ = As/bd = 3573/(1000 × 1800) = 0.001985 < 0.02

V_Rd,c = [0.12 × 1.33(100 × 0.001985 × 40)^(1/3)]=  0.318 N/mm²

Since V_Rd,c (0.318 N/mm²) > V_Ed (0.208 N/mm²), No shear reinforcement is required Okay.

Step 7: Check for Anchorage Length

Let us calculate the design tension anchorage length of H32mm bar (f_yk = 500 N/mm², concrete cover = 100 mm, Concrete cylinder strength f_ck = 40 N/mm²) for a bent bar assuming good bond conditions.

l_bd = α₁ α₂ α₃ α₄ α₅ l_b,req ≥ l_b,min
l_b,rqd = (ϕ/4) σ_sd/f_bd
f_bd =2.25η₁ η₂ f_ctd
η₁ = 1.0 ‘Good’ bond conditions
η₂ = 1.0 bar size ≤ 32

f_ctd = (α_ct f_{ctk 0.05})/γ_c

where;
f_{ctk 0.05} = characteristic tensile strength of concrete at 28 days = 2.5 N/mm² (Table 3.1 EC2)
γ_c = partial (safety) factor for concrete = 1.5
α_ct = coefficient taking account of long-term effects on the tensile strength, this is an NDP with a recommended value of 1.

f_ctd = (1.0 × 2.5)/1.5 = 1.667 N/mm²
f_bd = 2.25 × 1.0 × 1.0 × 1.667= 3.75 N/mm²

l_b,rqd = (ϕ/4) σ_sd/f_bd
σ_sd = 0.87 × 500 = 435 N/mm²

l_b,rqd = (ϕ × 435 )/(4 × 3.75) = 29ϕ

Therefore;

l_bd = α₁ α₂ α₃ α₄ α₅(29ϕ) (see Table 8.2 EC2)

For a bent bar
α₁ = 1.0 (C_d = 75 mm is ≤ 3ϕ = 3 × 32 = 96 mm)
α₂ = 1.0 – 0.15 (C_d – 3ϕ)/ ϕ = 0.901 < 1.0
α₃ = 1.0 conservative value with k = 0
α₄ = 1.0 N/A
α₅ = 1.0 conservative value
l_bd = 0.9 × (29ϕ) = 26.1ϕ = 26.1 × 32 = 835 mm

With the effective depth of 1800 mm, the pile dimension will satisfy the anchorage requirements.