Point of Contraflexure in Structures

A point of contraflexure in a structure is the point where the bending moment changes signs from positive to negative (and vice versa). In other words, it is a point where the nature of the bending moment transitions from sagging to hogging. The value of the bending moment at any point of contraflexure is zero.

For a section under a sagging moment, the bottom fibre of the member is under tension, therefore, reinforcements should be provided at the bottom of the section. For a section under a hogging moment, the top fibre is in tension, and reinforcement should be provided at the top. Therefore, the point of contraflexure provides good information on how reinforcements should be arranged in reinforced concrete structures.

There is no predetermined formula for determining the exact location where the point of contraflexure will occur in a structure. The location of the point of contraflexure on a structure depends on the type of load, loading arrangement, location of supports, and types of members. The easiest way to determine the point of contraflexure in any structure is to determine the equation for the bending moment, and equate it to zero. When the x-term (distance) in the equation is solved, the point of contraflexure is readily obtained.

[themoneytizer id=”98693-1″]

Contraflexure in beams

In simply supported beams, there is no point of contraflexure since the entire beam is expected to be sagging when subjected to any lateral load. However, when an overhang is introduced to a simply supported beam, a point of contraflexure will be developed as the bending moment transitions from hogging at the cantilever area, to sagging in the span area. Once again, the loading configuration and loading locations affect how the point of contraflexure will behave.

Let us consider the simply supported beam with overhang loaded as shown below;

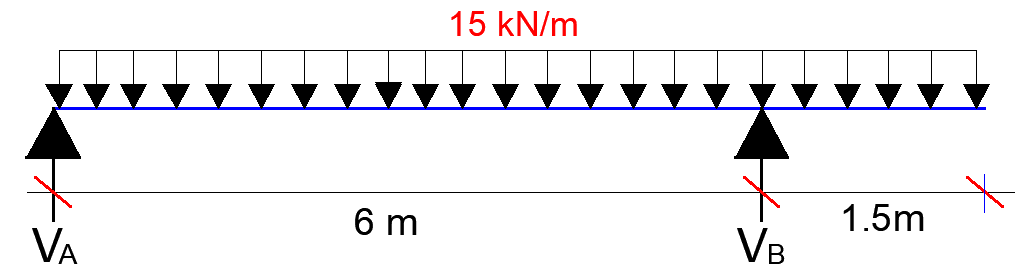
∑M_B = 0
6V_A – (15 × 6²)/2 + (15 × 1.5²)/2 = 0
V_A = 42.1875 kN

∑M_A = 0
6V_B – (15 × 7.5²)/2 = 0
V_B = 70.3125 kN

If we cut a section x-x along the span, the bending moment equation along the span is given by;

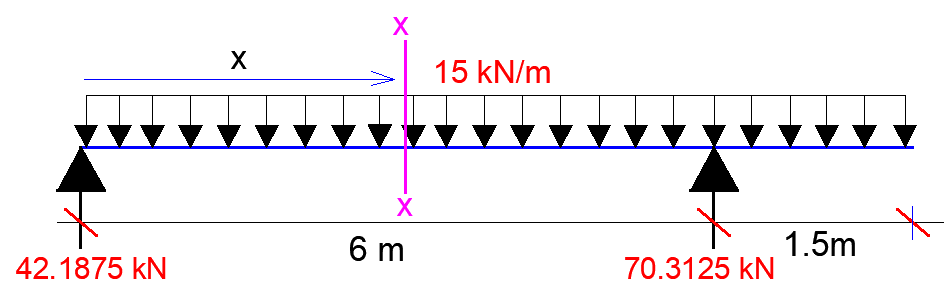
M_x = 42.1875x – 15x²/2 = 42.1875x – 7.5x²

We can obtain the point of contraflexure by equating the above equation to zero;

M_x = 42.1875x – 7.5x² = 0

Solving quadratically;
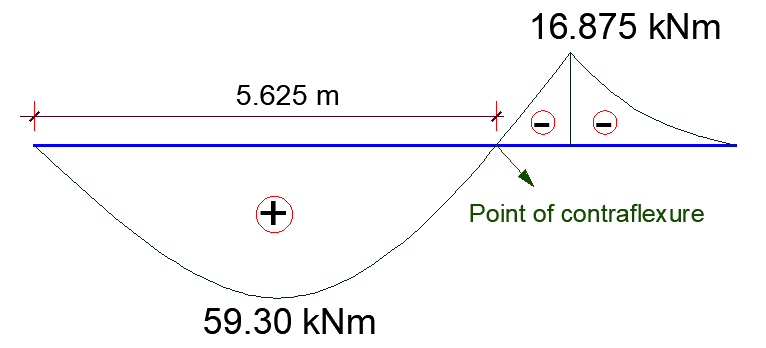
x = 5.625 m

Therefore, the point of contraflexure occurs at 5.625m from support A.

The maximum bending moment can be obtained by differentiating the bending moment equation (to obtain the equation for shear), and equating it to zero;

N/B: The maximum bending moment occurs at the point of zero shear.

∂Mx/∂x = 42.1875 – 15x = 0

Therefore; x = 2.8125 m
M_max = 42.1875(2.8125) – 7.5(2.8125)² = 59.3 kNm

Bending moment at support B;
M_B = 42.1875(6) – 7.5(6)² = -16.875 kNm

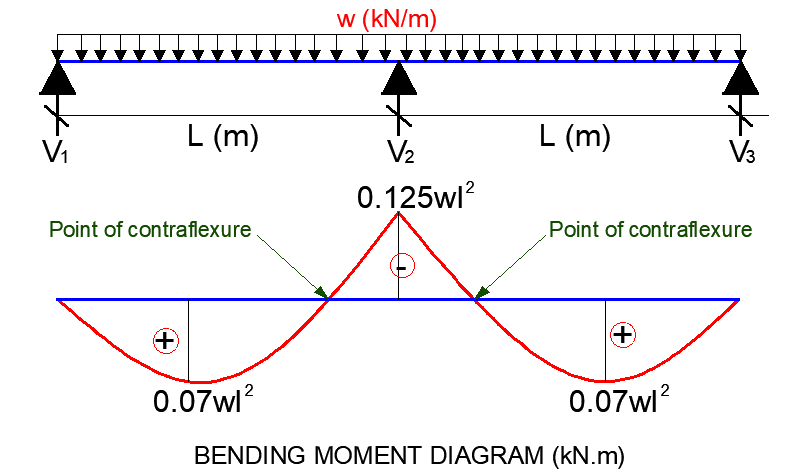
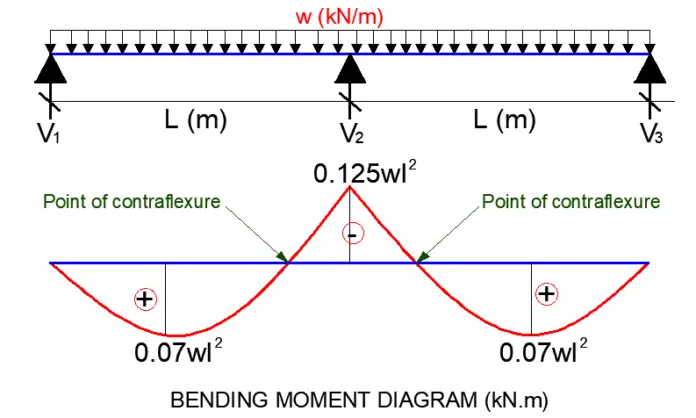
For continuous beams that are supported on pinned supports, it is expected that the hogging moments will occur at the intermediate supports, while the sagging moments will occur at the spans. Therefore, the points of contraflexure occur very close to the intermediate supports.

When a beam is fixed at one end, it is also expected that a point of contraflexure occurs close to the fixed support, as the bending moment transitions from hogging at the fixed support, to sagging in the span.

Contraflexure in frames

The point of contraflexure in frames is more complex than in beams. When the column of a frame is supported on a fixed support, a point of contraflexure is expected on the column. However, if the column is supported on a pinned support, there may be no point of contraflexure unless there is a lateral load on the column.

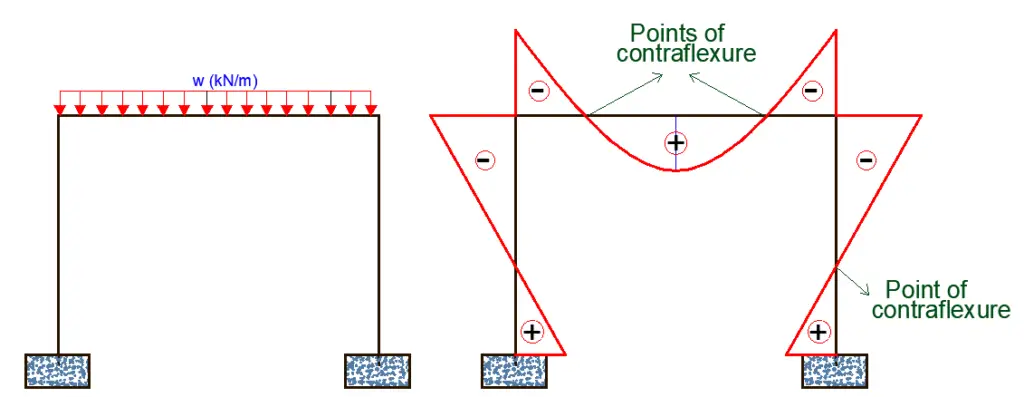
On the beams of a frame, points of contraflexure are also expected because of the inherent hogging moment that exists at the beam-column junctions of rigid frames. When the bending moment transitions from hogging at the beam-column junction to sagging at the beam spans, a point of contraflexure develops.

When carrying out approximate analysis of framed structures, the point of contraflexure for columns is usually assumed to occur at the mid-point, as a known point of zero bending moment.

Significance of the point of contraflexure

Points of contraflexure are very significant in the design of steel structures and reinforced concrete structures.

Reinforced Concrete Structures

In reinforced concrete structures, the points of contraflexure provide information on where the top reinforcements should be curtailed. For instance, it is reasonable to stop the top reinforcement at the support of beams at the point of contraflexure. In the detailing guidelines of beams, this is taken as 0.25L, while in the detailing of slabs, this is taken as 0.3L, where L is the length of the span.

Furthermore, since the bending moment at the point of contraflexure is zero, it could serve as a very good point where tension bars could be lapped without any serious consequences. This however should be used with caution since the actual loading in real-life structures can vary considerably. It is advisable to follow the detailing guidelines in the code of practice.

Steel Structures

The point of contraflexure also plays an important role in the design of steel structures. For instance, in the design of portal frames, the point of contraflexure can provide the needed information for the length of the haunches, which provides increased stiffness at the column-rafter junction. It may also be desirable to locate splices and joints at the point where the bending moment is zero, so as to have more economical joints.

The point of contraflexure and the shape of the moment diagram plays an important role in the design of steel structures for lateral torsional buckling.