How to Load Columns in RC Building Design

When carrying out the manual design of reinforced concrete structures, column loads are usually assessed by considering the support reactions from beams they are supporting, or by the tributary area method. The latter is more popular due to its simplicity and speed, but usually fails to capture all the loads that are imposed on the columns (such as wall loads), while the former is more complex and time-consuming, it usually very representative of all the possible loads that are imposed on the column.

Steps on how to load a column from beam support reaction

The following steps can be adopted when using beam support reactions to obtain the axial load on columns.

(1) Load the floor slab adequately, and factor the loads at ultimate limit state, using the appropriate load combination.

(2) Load all the beams that are connected to the column.

(3) Transfer the loads from slab to the beam using the appropriate relationship. Based on yield lines, the loads are usually triangular or trapezoidal, but this is cumbersome to analyse manually. An equivalent UDL (reasonably accurate) can be used to transfer slab loads to beams by employing the formulas below.

One way slabs
Long span   q = nl_x/2
Short slab q = nl_x/5

Two way slabs
Long span    q = nl_x/2(1 – 1/3k²)
Short span     q = nl_x/3

Where;
q =  Load transferred from slab to the beam
n = load at ultimate limit state
1.4g_k + 1.6q_k (BS 8110)
1.35g_k + 1.5q_k (Eurocode 2)
k = L_y/L_x
L_y = Length of long span of slab
L_x = Length of short span of the slab

(4) Analyse the floor beams completely using any suitable method of your choice, while also considering any additional load that may be on the beam such as wall load and finishes.

(5) Obtain the support reactions of the beam, which represents the load that is transferred from the floor to the column.

Design Example

In this post, the floor plan shown below is for a shopping complex, and it desired to obtain the column axial loads at ultimate limit state.

Design Data
Size of all columns = 230 x 230mm
Size of all beams = 450 x 230mm
Thickness of slab = 200mm
Unit weight of concrete = 25 kN/m³
Unit weight of sandcrete block = 3.47 kN/m²
f_ck = 25 N/mm²
f_yk = 500 N/mm²

Load combination = 1.35g_k + 1.5q_k
Design variable load (q_k) = 4 kN/m²

k = L_y/L_x = 6/5 = 1.2 (in all cases)
Only external beams are carrying block work load.

Load Analysis

Roof beam
Permanent load on roof beams g_k = 6 kN/m
Variable load on roof beam  q_k = 1.5 kN/m
(These values are assumed)
At ultimate limit state, n = 1.35(6) + 1.5(1.5) = 10.35 kN/m

Slab Load Analysis
Concrete own weight = 25 kN/m³  × 0.2m  = 5.0  kN/m²
Screeding and Finishes (say)    = 1.35  kN/m²
Partition allowance   = 1.5  kN/m²
Total (g_k)    =  7.85 kN/m²
Variable action (q_k)    = 4 kN/m²

n = 1.35gk + 1.5qk = 1.35(7.85) + 1.5(4) = 16.6 KN/m²

Wall load on beam
Unit weight of sandcrete block = 3.47 kN/m²
Height of wall = 3.5m
Wall load on beam =  3.47 kN/m²  × 3.5m  = 12.145  kN/m

Load on Beams
External Longitudinal beams (Axis 1:A-D and Axis 3:A-D)
Self weight of beam (factored) = 1.35 × 0.23m × 0.25m × 25 = 1.94 kN/m
Load from slab = nl_x/2(1 – 1/3k²) = [(16.6 × 5)/2] × (1 – 1/(3 ×1.2²)) = 31.893 kN/m
Load from block work = 12.145  kN/m
Total load = 45.978 kN/m

External Transverse beams (Axis A:1-3 and Axis D:1-3)
Self weight of beam (factored) = 1.35 × 0.23m × 0.25m × 25 = 1.94 kN/m
Load from slab = nl_x/3 = (16.6 × 5)/3 = 27.667 kN/m
Load from block work = 12.145  kN/m
Total load = 41.752 kN/m

Internal Longitudinal Beam (Axis 2:A-D)
Self weight of beam (factored) = 1.35 × 0.23m × 0.25m × 25 = 1.94 kN/m
Load from slab = nl_x/2(1 – 1/3k²) = [(16.6 × 5)/2] × (1 – 1/(3 ×1.2²)) = 2 × 31.893 kN/m = 63.786 kN/m (we multiplied by two because this beam is receiving slab load from two directions.)
Load from block work = 0 (there are no block works inside the building)
Total load = 65.726 kN/m

Internal Transverse beams (Axis B:1-3 and Axis C:1-3)
Self weight of beam (factored) = 1.35 × 0.23m × 0.25m × 25 = 1.94 kN/m
Load from slab = nlx/3 = (16.6 × 5)/3 = 2 × 27.667 kN/m = 55.334 kN/m (slab load is coming from two directions)
Load from block work = 0
Total load = 57.274 kN/m

Self weight of Columns
Self weight of column (factored) = 1.35 × 0.23m × 0.23m × 3.75m × 25 kN/m³ = 6.695 kN

Structural Analysis
A little consideration will show that the support reactions for the floor beams (equal spans) can be obtained by considering the shear force coefficients given below;

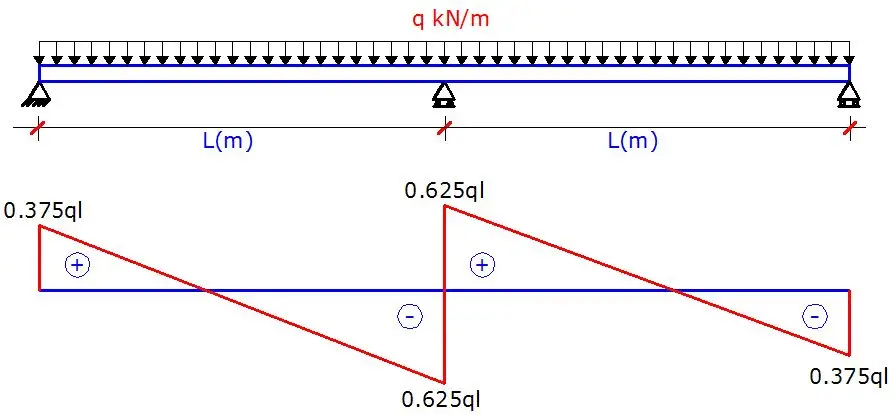
Fig 4: Shear force coefficient (3 span beam)

Load Analysis of Column A1
1st Floor
Load from longitudinal roof beam (1:A-D) = 0.4 × 10.35 kN/m × 6m = 24.84 kN
Load from transverse roof beam (A:1-3) = 0.375 × 10.35 kN/m × 5m = 19.41 kN
Self weight of column = 6.695 kN
Total = 50.945 kN

Ground Floor
Load from above = 50.945 KN
Load from longitudinal floor beam (1:A-D) = 0.4 × 45.978 kN/m × 6m = 110.347 kN
Load from transverse floor beam (A:1-3) = 0.375 × 41.752 kN/m × 5m = 78.285 kN
Self weight of column = 6.695 kN
Total = 246.272 kN

Load Analysis of Column A2
1st Floor
Load from longitudinal roof beam (2:A-D) = 0.4 × 10.35 kN/m × 6m = 24.84 kN
Load from transverse roof beam (A:1-3) = 2(0.625 × 10.35 kN/m × 5m) = 64.687 kN
Self weight of column = 6.695 kN
Total = 96.222 kN

Ground Floor
Load from above = 96.222 KN
Load from longitudinal floor beam (2:A-D) = 0.4 × 65.726 kN/m × 6m = 157.742 kN
Load from transverse floor beam (A:1-3) = 2(0.375 × 41.752 kN/m × 5m) = 156.57 kN
Self weight of column = 6.695 kN
Total = 417.229 kN

Load Analysis of Column B1
1st Floor
Load from longitudinal roof beam (1:A-D) = (0.5 × 10.35 kN/m × 6m) + (0.6 × 10.35 kN/m × 6m) = 68.31 kN
Load from transverse roof beam (B:1-3) = 0.375 × 10.35 kN/m × 5m = 19.41 kN
Self weight of column = 6.695 kN
Total = 94.415 kN

Ground Floor
Load from above = 94.415 KN
Load from longitudinal floor beam (1:A-D) = (0.5 × 45.978 kN/m × 6m) + (0.6 × 45.978 kN/m × 6m)   = 303.455 kN
Load from transverse floor beam (B:1-3) = 0.375 × 57.274 kN/m × 5m = 107.388 kN
Self weight of column = 6.695 kN
Total = 511.953 kN

Load Analysis of Column B2
1st Floor
Load from longitudinal roof beam (2:A-D) = (0.5 × 10.35 kN/m × 6m) + (0.6 × 10.35 kN/m × 6m)= 68.31 kN
Load from transverse roof beam (A:1-3) = 2(0.625 × 10.35 kN/m × 5m) = 64.687 kN
Self weight of column = 6.695 kN
Total = 139.692 kN

Ground Floor
Load from above = 139.692 kN
Load from longitudinal floor beam (2:A-D) = (0.5 × 65.726 kN/m × 6m) + (0.6 × 65.726 kN/m × 6m)  = 433.7916 kN
Load from transverse floor beam (A:1-3) = 2(0.625 × 57.274 kN/m × 5m) = 357.9625 kN
Self weight of column = 6.695 kN
Total = 938.141 kN

As you can see, that was very straightforward with the use of shear force coefficients, given the fact that the beams were of equal span. When the beams are not equal, you have to carry out the analysis, and transfer the shear forces accurately. Now, let us compare load analysis of column B2, by the tributary area method.

Thank you for visiting, join the Structville Interaction on Facebook by visiting;
www.facebook.com/structville