In cohesionless soils, it is challenging to collect undisturbed samples, so we usually rely on the outcomes of in-situ testing (SPT or CPT tests) to determine the total settlement. Moreover, as the allowable soil pressure in these soils is determined more by considerations of settlement than bearing capacity failure, it is desirable to predict them accurately.
The average value of N to be used in the assessment of settlements and bearing capacity is determined by taking the SPT corrected values at foundation level N1, depth 1.5B (N2), and depth 2B (N3).
N = (3N1 + 2N2 + N3)/6 ——— (1)

The total settlement of a foundation can be divided into the following three components:
- The immediate settlement ∆ which takes place due to elastic deformation of soil without change in water content.
- The consolidation settlement ∆H which takes place in clayey soil mainly due to the expulsion of the pore water in the soil.
- Secondary (creep) settlement ∆S which takes place over long periods due to the viscous resistance of soil under constant compression.
The immediate settlement is usually considered for footings on sand (cohesionless soils).
Correlation from Terzaghi and Peck
From Terzaghi and Peck’s (1967) correlation of settlement with SPT values, Teng (1969) proposed the following expression for the load for a given settlement of a footing of breadth B in a sand deposit with an SPT value of N:
For ∆ = 25 mm; p = 34.6(N – 3)[(B + 0.3)/2B]2 (in kN/m2) ——— (2)
for ∆ = 1 mm; p = 1.385(N – 3)[(B + 0.3)/2B]2 (in kN/m2) ——— (3)
Hence the settlement in mm for a load q in kN/m2 is as follows:
∆ = (0.722q/(N – 3)) × [(B + 0.3)/2B]2 (in mm) ——— (4)
As it was found that Eq. (4) gives high values of settlements, Meyerhof proposed the following:
Actual settlement = settlement by Eq.(4)/1.5 ——— (5)
Meyerhof’s Formula Based on SPT Values for Cohesionless Soils
Meyerhof noted that Terzaghi and Peck’s correction overestimates the actual settlement considerably. He proposed the following formula based on SPT tests for settlement in mm for q in kN/m2 and B in meters;
∆ = 1.6q/N for B < 1.25 m
∆ = 2.84q/N × [B/(B + 0.3)]2 for B > 1.25 m
∆ = 2.84q/N for large rafts
From test results, we know that in cohesionless soil, for the same intensity of load, the settlement of a footing increases with its width according to the following formula. (The settlement beyond B = 4 m can be taken as more or less constant.)
s = s1[2B/(B + 0.3)]2
where B is the breadth in meters and s1 is the settlement of a 0.3 m square plate.
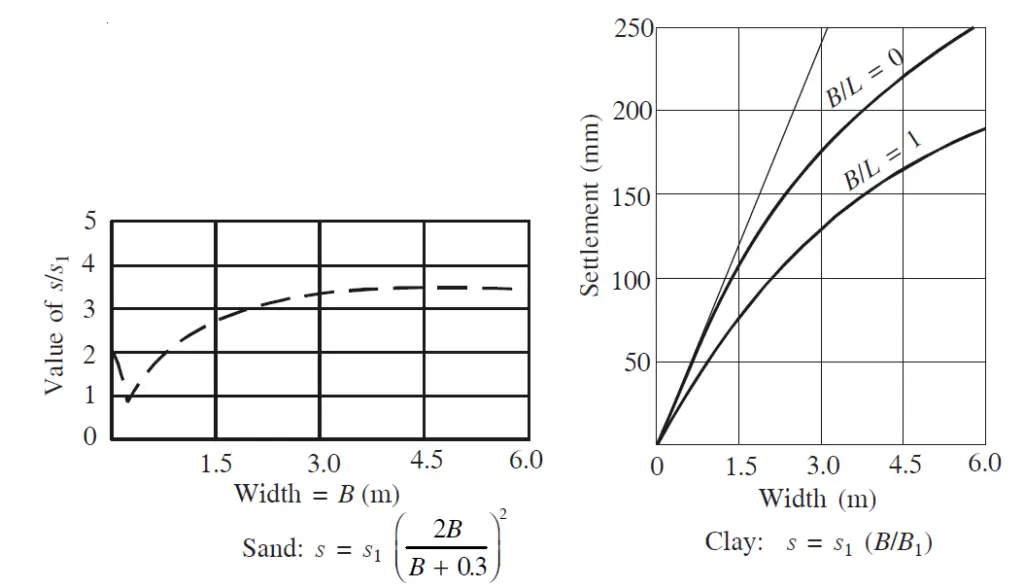
Another important empirical relation that Terzaghi established from his observation is that in both strip footing and also in pad footings of equal size and equally loaded the differential settlement that can be expected in all types of soil is about 50 percent of the maximum expected settlement of these footings.
In actual practice, the sizes of the footings can also be different. Hence in real-field situations, we may assume that the maximum expected differential settlement will be roughly 75% of the expected maximum settlement. Accordingly, if we assume an allowable differential settlement of 18 mm (3/4 inch) the maximum settlement we can allow in the footing will be 25 mm (1 inch).
In 1969, Teng proposed the following important relation between the settlement of a footing in sand and its SPT value N. [See Eq. (4)]
∆ = (0.722q/(N – 3)) × [(B + 0.3)/2B]2 (in mm)
where;
s = settlement in mm
q = intensity of load in kN/m2
B = breadth of footing in metres.
From the above, the net load required for 1 mm settlement will be as follows:
∆ = 1.385(N – 3)[(B + 0.3)/2B]2 (in kN/m2 per mm settlement)
where;
q1 = bearing pressure for 1 mm settlement in kN/m2
N = corrected SPT value
B = width of the footing in metres.
For 25 mm settlement, we get the following equation as the net allowable bearing pressure in kN/m2.
qnet = q25 = 34.6(N – 3)[(B + 0.3)/2B]2 = 8.6(N – 3)[(B + 0.3)/B]2 (in kN/m2)
Taking B = 4 m,
qnet = 10(N – 3) (approx.)
To this, we can add the effect of depth. Peck, Hanson and Thornburn (1974) used this relation to plot the graph for safe bearing capacity in sands for N values. The value of [(B + 0.3)/2B]2 decreases rapidly with B as shown in Fig. 3, so that the empirical value of qa for cohesionless soils with a variation of B can be expressed in kN/m2 as follows:
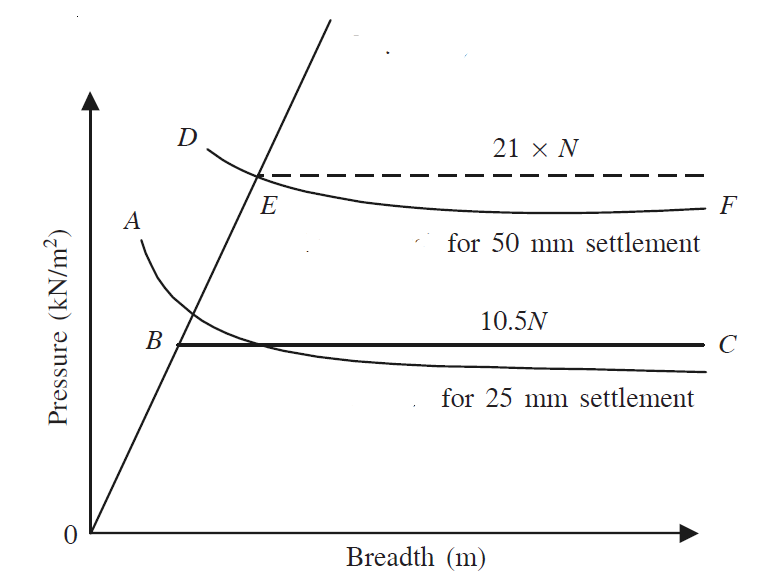
Therefore;
qa = 10.5NB (for B < 1 m for 25 mm settlement)
qa = 10.5N (for B > 1 m for 25 mm settlement)
qa = 0.42N (kN/m2) (approx.) for 1 mm settlement for B > 1 m.
An average value of N for a depth B below the footing is taken as the N value for the calculation of bearing capacity.
References
Terzaghi, K. and Peck, R.B. (1967): Soil Mechanics in Engineering Practice, John Wiley & Sons, New York, 1967
Teng, W.C. (1969): Foundation Design, Prentice-Hall of India, New Delhi
Peck, R.B., Hanson, W.E., and Thornburn, T.H., (1974): Foundation Engineering, John Wiley & Sons
Varghese P.C. (2012): Foundation Engineering. PHI Learning Private Limited, New Delhi










