Design of Cantilever Retaining Wall Supporting Lateritic Earth Fill

By

-

July 28, 2022

Table of Contents

Cohesive soil profiles due to their nature are partially self supporting up to an extent called the critical depth (the critical depth is given by 2Z_o, kindly see figure above). As a result, such soils would not exert much pressure on a retaining wall as a granular material would (especially considering active earth pressure). Tropical laterites (especially those found in Nigeria) usually possess angle of internal friction and some cohesion. Their usage for construction purposes is also widespread.

The walls retaining such soils are subjected to active and passive pressure. In this example, we are going to consider active pressure only (all passive pressure neglected), but note that passive pressure could be more critical and hence govern the design (I recommend you read standard geotechnical engineering textbooks for more knowledge on this subject).

Worked Example

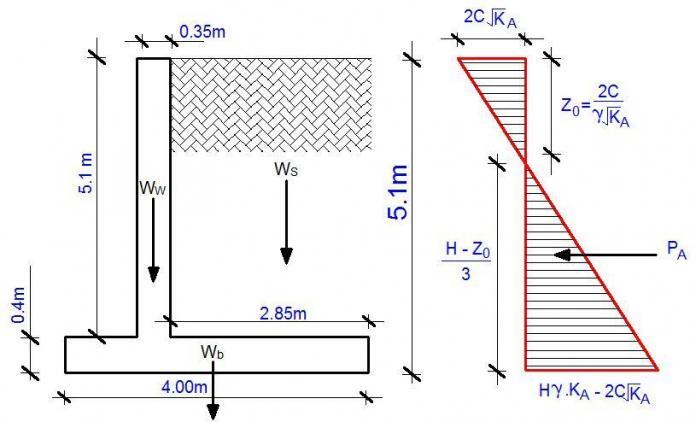
The cantilever retaining wall shown below is backfilled with tropical lateritic earthfill, having a unit weight, ρ, of 18 kN/m³, a cohesion C of 8 kN/m³ and an internal angle of friction, φ, of 26°. The allowable bearing pressure of the soil is 150 kNm/², the coefficient of friction is 0.5, and the unit weight of reinforced concrete is 24 kN/m³. Water level is at a great depth and adequate drainage is provided at the back of the wall.

We are to;
1. Determine the factors of safety against sliding and overturning for the active pressure.
2. Calculate ground bearing pressures.
3. Design the wall and base reinforcement assuming f_cu = 30 N/mm², f_y = 460 N/mm² and the cover to reinforcement in the wall and base are, respectively, 40 mm and 50 mm.

Geotechnical Design

Wall Pressure Calculations

Retaining wall with lateritic earth fill

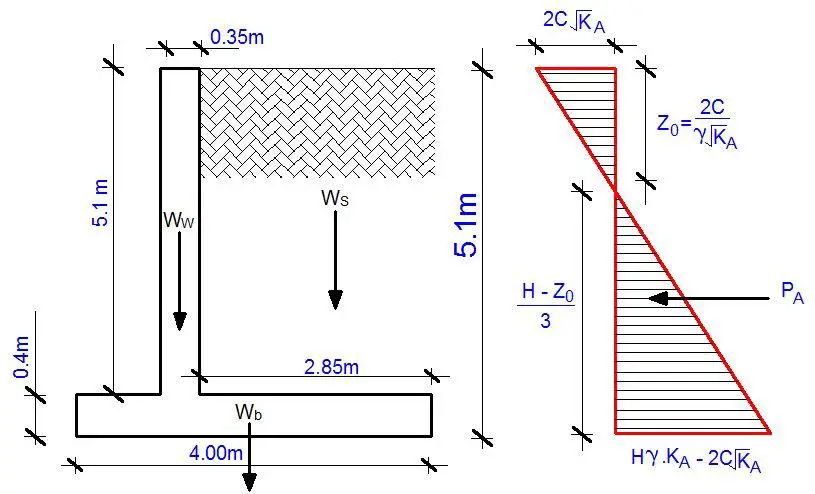
Coefficient of active pressure K_A
Using Rankine’s theory
K_A = (1 – sinφ) / (1 + sinφ);
K_A = (1 – sin 26°) / (1 + sin 26°) = 0.39046;

Pressure at the top of wall = 2C√K_A = 2 × 8 × √0.39046 = 9.998 kN/m²
Z₀ = 2 C/γ√K_A = (2 × 8)/(18 × √0.39046) = 1.423m

Pressure at the bottom of retaining wall = H.γ.K_A – 2C√K_A = (5.5 × 18 × 0.39046) – (2 × 8 × √0.39046) = 32.408 kN/m²

Resistance to Sliding

Consider the forces acting on a 1 m length of wall. Horizontal force on wall due to backfill, P_A, is;
P_A = 0.5 × 32.408 × 4.077 = 66.063 kN/m

Weight of wall (W_w) = 0.35 × 5.1 × 24 = 42.84 kN/m
Weight of base (W_b) = 0.4 × 4 × 24 = 38.4 kN/m
Weight of soil (W_s) = 2.85 × 5.1 × 18 = 261.63 kN/m
Total vertical force (W_t) = 324.87 kN/m

Friction force, F_F, is
F_F = μWt = 0.5 × 324.87 = 171.435 kN/m

Neglecting all passive pressure force (F_P) = 0.
Hence factor of safety against sliding is;
F.O.S = F_F/P_A = 171.435/66.063 = 2.595
The factor of safety 2.595 > 1.5. Therefore the wall is very safe from sliding.

Resistance to Overturning

Taking moments about the toe, sum of overturning moments (M_O) is;
M_O = (66.063 kN/m) × (4.077/3) = 89.779 kN.m

Sum of Restoring Moment M_R;
M_R = (W_w × 0.975m) + (W_b × 2m) + (W_s × 2.575m)
M_R = (42.84 × 0.975m) + (38.4 × 2m) + (261.63 × 2.575m) = 792.266 kNm

F.O.S = M_R / M_O = 792.266/89.779 = 8.824
The factor of safety 8.824 > 2.0. Therefore the wall is very safe from overturning.

Bearing Capacity Check

Bending moment about the centre line of the base;
M = [66.064 × (4.077/3)] + (W_w × 1.025m) – (W_s × 1m)
M = [66.064 × (4.077/3)] + (42.84 × 1.025m) – (261.63 × 0.575m) = -16.745 kNm

Total vertical load = 324.87 kN

The eccentricity (e) = M/N = (16.745/324.87) = 0.0515m

Let us check D/6 = 4/6 = 0.666
Since e < D/6, there is no tension in the base

The maximum pressure in the base;
q_max = P/B (1 + 6e/B) = 324.87/4 [1 + (6 × 0.0515)/(4)] = 87.491 KN/m²
87.491 KN/m² < 175 KN/m²
Therefore, the bearing capacity check is satisfied.

Structural Design

Design of the Wall

Conservatively taking the moment at the base of the wall due to the active force;
M = [66.064 × (4.077/3)] = 89.781 kN.m
At ultimate limit state M = 1.4 × 89.781 = 125.693 kN.m

Thickness of wall = 350mm

Effective depth = 350 – 40 – (8) = 302mm (assuming Y16mm bars will be employed for the construction)

k = M/(F_cubd²) = (125.693 × 10⁶) / (30 × 1000 × 302²) = 0.0459
k < 0.156, no compression steel needed
la = 0.5 + (0.25 – k/0.9)^0.5 = 0.5 + (0.25 – 0.0459/0.9)^0.5 = 0.946
A_Sreq = M/(0.95F_y.la.d ) = (125.693 × 10⁶) / (0.95 × 460 × 0.946 × 302) = 1006 mm²/m
A_Smin = (0.13bh)/100 = (0.13 × 1000 × 350) / 100 = 455 mm²
Provide Y16 @ 150mm c/c (A_sprov = 1340 mm²/m)

Check for shear
Design shear force on wall at ultimate limit state V = (1.4 × 66.064) = 92.4896 kN/m
Shear stress v = V/bd = (92.4896 × 1000) / (1000 × 302) = 0.3062 N/mm²
V_c = 0.632 (100A_s/bd)^1/3 (400/d)^1/4
Vc = 0.632 × [(100 × 1340)/(1000 × 302)]^1/3 × (400/302)^1/4
Vc = 0.632 × 0.7627 × 1.0727 = 0.517 N/mm²
For F_cu = 30N/mm², Vc = 0.517 × (30/25)^1/3 = 0.5494 N/mm²
Since v < Vc, no shear reinforcement required.

Design of the Base

The pressure distribution diagram on the base at serviceability limit state is as shown below;
q_max = P/B (1 + 6e/B) = 324.87/4 [1 + (6 × 0.0515)/(4)] = 87.491 kN/m²
q_min = P/B (1 – 6e/B) = 324.87/4 [1 – (6 × 0.0515)/(4)] = 74.927 kN/m²

At ultimate limit state;
q_max = 1.4 × 87.491 = 122.487 KN/m²
q_min = 1.4 × 74.927 = 104.898 KN/m²
q_C = 104.898 + [2.85 (122.487 – 104.898)]/4 = 117.430 kN/m²
q_B = 104.898 + [3.2 (122.487 – 104.898)]/4 = 118.968 kN/m²

On investigating the maximum design moment about point C;

Back fill = 1.4 (18 × 5.1 × 2.85 × 2.85/2) = -521.952 kNm
Heel Slab = 1.4 (24 × 0.4 × 2.85 × 2.85/2) = -54.583 kNm
Earth Pressure = (104.898 × 2.85 × 2.85/2) + [(117.430 – 104.898) × 0.5 × 2.85 × 2.85/3] = 426.017 + 16.965 = 442.982 KNm
Net moment = -521.952 – 54.583 + 442.982 = -133.553 kNm

On investigating the maximum design moment about point B;

Back fill = (conservatively neglected)
Heel Slab = 1.4 (24 × 0.4 × 0.8 × 0.8/2) = – 4.3008 kNm
Earth Pressure = (118.968 × 0.8 × 0.8/2) + [(122.487 – 118.968) × 0.5 × 0.8 × (2 × 0.8/3)] = 37.9776 + 0.751 = 38.727 kNm
Net moment = -4.3008 + 38.727 = 34.426 kNm

Design of the toe
M_B = 133.553 kN.m

Thickness of base = 400 mm

Effective depth = 400 – 50 – (8) = 342 mm (assuming Y16mm bars will be employed for the construction)

k = M/(F_cubd²) = (133.553 × 10⁶) / (30 × 1000 × 342²) = 0.0385
k < 0.156, no compression steel needed
la = 0.5 + (0.25 – k/0.9)^0.5 = 0.5 + (0.25 – 0.0385/0.9)^0.5 = 0.95
A_Sreq = M/(0.95F_y.la.d ) = (133.553 × 10⁶) / (0.95 × 460 × 0.95 × 342) = 941 mm²/m
A_Smin = (0.13bh)/100 = (0.13 × 1000 × 400) / 100 = 520 mm²
Provide Y16 @ 175 mm c/c Top (A_sprov = 1148 mm²/m)

Design of the heel
M_C = 34.426 KNm

Thickness of base = 400 mm
Effective depth = 400 – 50 – (6) = 344 mm (assuming Y12mm bars will be employed for the construction)

k = M/(F_cubd²) = (34.426 × 10⁶) / (30 × 1000 × 344²) = 0.00981
k < 0.156, no compression steel needed
la = 0.5 + (0.25 – k/0.9)^0.5 = 0.5 + (0.25 – 0.00981/0.9)^0.5 = 0.95
A_Sreq = M/(0.95F_y.la.d ) = (34.426 × 10⁶) / (0.95 × 460 × 0.95 × 344) = 242 mm²/m
A_Smin = (0.13bh)/100 = (0.13 × 1000 × 400) / 100 = 520 mm²
Provide Y12 @ 175mm c/c (A_sprov = 646 mm²/m)

Check for shear at the base
The maximum shear force at ‘d’ from the face of the wall is investigated at the either side;

Maximum shear force at point B
Earth fill = 1.4 × 18 × 5.1 × 2.85 = -366.282 kN/m
Wall base = 1.4 × 24 × 0.4 × 2.85 = -38.304 kN/m
Base Earth Pressure = 0.5 (104.898 + 117.430) × 2.85 = 316.817 kN/m
Net shear force = -366.282 – 38.304 + 316.817 = -87.769 kN/m

A little investigation will show that this is the maximum shear force at any section on the base.

Taking the maximum shear stress at the base v = (87.769 × 1000) / (1000 × 342) = 0.2566 N/mm²

V_c = 0.632 (100As/bd)^1/3 (400/d)^1/4
Vc = 0.632 × [(100 × 1148) / (1000 × 342)]^1/3 × (400/342)^1/4
Vc = 0.632 × 0.694 × 1.0399 = 0.456 N/mm²
For F_cu = 30N/mm², Vc = 0.456 × (30/25)^1/3 = 0.484 N/mm²
Since v < Vc, no shear reinforcement required.

DETAILING
I will need my readers to do the detailing sketches. I will accept both manual (hand) and CAD details. But your manual sketches must be very neat and well scaled. You should show the plans and at least one section. If your detailing is good enough, I will publish it on this post with your Facebook, LinkedIn, or G+ URL attached.

So, I will keep updating the post with as many good pictures as I receive. Good knowledge for all to flourish @ Structville

Send your sketches and URL profile to info@structville.com

Thank you for visiting Structville…

Our Facebook page is at www.facebook.com/structville

Analysis of Arch-Frame Structure with Tie Element: A solved Example

By

Ubani Obinna Uzodimma

-

February 16, 2020

An arch is supported on frame with different levels of supports as shown above. The frame is supported on a hinge at support A and a roller at support C. A tie beam is used to connect node B and support C. Plot the bending moment, shear force, and axial force diagram die to the externally applied load.

Solution

Support Reactions

∑M_C = 0
30Ay – 10Ax – (10 × 30²)/2 = 0
30Ay – 10Ax = 4500 ————- (1)

∑F_X = 0
Ax + 25 = 0
Ax = -25 kN (pointing in the reverse of assumed direction)

Plugging the value of Ax into equation (1);
30Ay – 10(-25) = 4500
30Ay = 4250
Ay = 141.667 kN

∑M_A = 0
30Cy – (25 × 10) – (10 × 30²)/2 = 0
30Cy = 4750
Cy = 158.333 kN

∑M_D^R = 0

15Cy – (H × 5) – (10 × 15²)/2 = 0
15(158.333) – 5H – (10 × 15²)/2 = 0
– 5H + 1250 = 0
H = 250 kN

Geometric Properties of the Arch Section

The ordinate of the arch at any given horizontal length section is given by;

y = [4y_c (Lx – x²)] / L²
Where y_c is the height of the crown of the arch
y = [(4 × 5) × (30x – x²)]/30² = (2/3)x – (x²/45)

dy/dx = y’ = 2/3 – 2x/45

At x = 0; y = 0
y’ = 2/3 – 0/8 = 0.667
sin⁡θ = y’/√(1 + y’²) = 1/√(1 + 0.667²) = 0.5546
cos⁡θ = 1/√(1 + y’²) = 1/√(1 + 0.667²) = 0.8319

At x = 7.5m;
y = (2/3)x – (x²/45) = (0.667 × 7.5) – (7.5²/45) = 3.75m
y’ = 2/3 – 2(7.5)/45 = 0.333
sin⁡θ = y’/√(1 + y’²) = 0.333/√(1 + 0.333²) = 0.43159
cos⁡θ = 1/√(1 + y’²) = 1/√(1 + 0.333²) = 0.9487

At x = 15 m;
y = (2/3)x – (x²/45) = (0.667 × 15) – (15²/45) = 5.00m
y’ = 2/3 – 2(15)/45 = 0
sin⁡θ = y’/√(1 + y’²) = 0/√(1 + 0²) = 0
cos⁡θ = 1/√(1 + y’²) = 1/√(1 + 0²) = 1.0

At x = 22.5m;
y = (2/3)x – (x²/45) = (0.667 × 22.5) – (22.5²/45) = 3.75m
y’ = 2/3 – 2(22.5)/45 = -0.333
sin⁡θ = y’/√(1 + y’²) = -0.333/√(1 + 0.333²) = -0.43159
cos⁡θ = 1/√(1 + y’²) = 1/√(1 + 0.333²) = 0.9487

At x = 30m; y = 0
y’ = 2/3 – 2(30)/45 = -0.667
sin⁡θ = y’/√(1 + y’²) = -0.667/√(1 + 0.667²) = -0.5546
cos⁡θ = 1/√(1 + y’²) = 1/√(1 + 0.667²) = 0.8319

Internal Stresses in the Arch Structure
Bending Moment
M_A = 0
M_B^B= (25 × 10) = 250 kN.m
M_B^UP= (25 × 10) = 250 kN.m
M₁ = (141.667 × 7.5) + (25 × 13.75) – (25 × 3.75) – (10 × 7.5²)/2 – (250 × 3.75) = 93.7525 kN.m
M_D = (141.667 × 15) + (25 × 15) – (25 × 5) – (10 × 15²)/2 – (250 × 5) = 0

Coming from the right
M₂ = (158.333 × 3.75) – (250 × 5) – (10 × 12²)/2 = -31.252 kN.m
M_C = 0

Shear force

Section A – B (Column)
Q_A– Ax = 0
Q_A– 25 = 0
Q_A– Q_B^B = 25 kN

Q_i = ∑V cos⁡θ – ∑H sin⁡θ (for arch section)

Note that the horizontal forces of 25 kN will eliminate each other;

Q_B^UP = (141.667 × 0.8319) – (250 × 0.5546) = -20.797 kN
Q₁^R = Q₁^L = [141.667 – (10 × 7.5)] × 0.9487 – (250 × 0.43159) = -44.651 kN
Q_D = [141.667 – (10 × 15)] × 1.0 – (250 × 0) = -8.333 kN
Q₂^R = Q₂^L = [141.667 – (10 × 22.5)] × 0.9487 – (250 × –0.43159) = 28.839 kN
Q_C = [141.667 – (10 × 30)] × 0.8319 – (250 × -0.5546) = 6.932 kN

Axial force
Member AB = 141.667 kN (compression)
Member BC = 250 kN (Tension)

For the arch section;
N_i = -∑V sin⁡θ – ∑H cos⁡θ
N_B^UP = -(141.667 × 0.5546) – (250 × 0.8319) = -286.543 KN (Compression)
N₁^L = -[141.667 – (10 × 7.5)] × 0.43159 – (250 × 0.9487) = -265.848 KN
N_D = -[141.667 – (10 × 15)] × 0 – (250 × 1) = -250 KN (Compression)
N₂^L = N₃^R = -[141.667 – (10 × 22.5)] × -0.43159 – (250 × 0.9487) = -273.141 KN
N_C = -[141.667 – (10 × 30)] × -0.5546 – (250 × 0.8319) = -295.786 KN

Internal Stresses Diagram

Thank you for visiting Structville.

Connect with our facebook page at www.facebook.com/structville

What is wrong with this section structural detailing?

By

Ubani Obinna Uzodimma

-

February 16, 2020

A section of a beam profile is shown above. BASED ON THE GIVEN DATA ONLY AND WITHOUT MAKING ANY ASSUMPTIONS, identify the technical error(s) in the section detailing using BS 8110-1:1997 recommendations? Read the hints below carefully!

Data
Figured dimensions are in mm
Concrete cover at the sides and the soffit = 40 mm
Concrete cover at the top = 30 mm
Strength of reinforcement = 460 N/mm²
Strength of concrete = 35 N/mm²
Section is at mid-span (sagging moment)
Area of tension reinforcement required = 2960 mm²

Hints:
(1) This post is for educational purposes, hence, your reply is better dropped here on Structville as a comment so that every person accessing the post from different platforms can see the reply.

(2) Please, do not guess. If you identify the error(s), kindly drop your comment, otherwise, keep checking back for other people’s replies. Do not post your guesses.

(3) If you are not familiar with BS 8110-1:1997, but you identify any error based on the code that you are familiar with, kindly state the code, and the error you discovered. Try to be technical in your explanations, or quote the requirement as given in the code.

(4) The diagram is not to scale, so use the figured dimensions only. Also, do not call on any data or information that is not provided.

(5) Let your explanations be offered with love.

We believe that knowledge is power.
Kindly tag all structural engineers you know and/or forward this post to them.

Our facebook page is at www.facebook.com/structville

Analysis and Design of Curved Circular Beams in a Reservoir

By

Ubani Obinna Uzodimma

-

October 27, 2020

Beams that are curved in plan are often found in buildings, circular reservoirs, bridges, and other structures with curves. Curved beams always develop torsion (twisting) in addition to bending moment and shear forces because the center of gravity of loads acting normal to the plane of the structure lies outside the lines joining its supports. Therefore to maintain equilibrium in the structure, the supports of a curved beam must be fixed or continuous.

In this post, we are going to show in the most simplified manner, how to analyse continuous circular (ring) beams.

circular beam in a reservoir — Circular beam supporting an overhead water tank

For ring beams;
Maximum Negative Moment at any support = K₁wr²
Maximum Positive Moment at any span = K₂wr²
Maximum Torsional Moment = K₃wr²
Total load on each column (support reaction) R = wr(2θ)

Shear force at any support = R/2 = wrθ

The coefficients are given in the table below;

Coefficients%2Bfor%2Bcurved%2Bbeams — **Source:** Table 21.1, Hassoun and Al-Manaseer (2008)

Solved Example
A cylindrical reservoir with a diameter of 6m is supported by a ring beam, which is supported on 8 equidistant columns. It is desired to analyse and design the ring beam to support the load from the superstructure.

The plan view of the structural disposition of the reservoir is shown below;

Load Analysis

(a) Geometry of sections
Dimension of beams = 450mm x 300mm
Dimension of column = ϕ300mm circular columns
Thickness of reservoir walls = 250mm
Thickness of reservoir slab = 250mm

(b) Density of materials
Density of stored material = 10 kN/m³
Density of concrete = 25 kN/m³

(c) Dead Loads
Weight of the walls = (25 kN/m³ × 0.25m × 4.75m × 18.849m) = 559.579 kN
Weight of bottom slab = (25 kN/m³ × 0.25m × 28.274m²) = 176.7125 kN
Weight of water stored = (10 kN/m³ × 4.5m × 23.758m²) = 1069.11 KN
Total = 1805.4015 kN

Let us transfer this load to the the ring beam based on the perimeter.

Perimeter of ring beam = πd = π × 6 = 18.849m

w = 1805.4015 kN / Perimeter of ring beam = 1805.4015 kN / 18.849m = 95.782 kN/m

Self weight of the beam = 25 kN/m³ × 0.3m × 0.45m = 3.375 kN/m

Total dead load on beam = 95.782 kN/m + 3.375 kN/m = 99.157 kN/m

Factoring the load on the beams at ultimate limit state = 1.35 × 99.157 kN/m = 133.862 kN/m

From the table above;
Number of supports (n) = 8
θ = π/n = 45°
K₁ = 0.052
K₂ = 0.026
K₃ = 0.0040
Radius (r) = 3m

Maximum Negative Moment at the supports = K₁wr²= -0.052 × 133.862 × 3² = -62.647 KN.m

Maximum Positive Moment at the spans = K₂wr²= 0.026 × 133.862 × 3² = 31.323 KN.m

Maximum Torsional Moment = K₃wr²= 0.0040 × 133.862 × 3² = 4.819 KN.m

Shear force at the supports = R/2 = wrθ = 133.862 × 3 × (π/8) = 157.7 KN

Structural Design
Design strength of concrete f_ck= 35 N/mm²
Yield strength of reinforcement f_yk= 500 N/mm²
Nominal cover to reinforcement = 30 mm

Span
M_Ed = 31.323 kN.m

Effective depth (d) = h – C_nom – ϕ/2 – ϕlinks
Assuming ϕ12 mm bars will be employed for the main bars, and ϕ8mm bars for the stirrups (links)
d = 450 – 30 – 6 – 8 = 406 mm

k = M_Ed/(f_ckbd²) = (31.323 × 10⁶)/(35 × 300 × 406²) = 0.0181
Since k < 0.167, no compression reinforcement required
z = d[0.5+ √(0.25 – 0.882K) ] = z = d[0.5+ √(0.25 – 0.882(0.0181))] = 0.95d

A_s1 = M_Ed/(0.87_yk z) = (31.323 × 10⁶)/(0.87 × 500 × 0.95 × 406) = 186.69 mm²
Provide 3H12 mm BOT (AS_prov = 339 mm²)

Supports
M_Ed = 62.647 KN.m

Effective depth (d) = h – C_nom – ϕ/2 – ϕlinks
Assuming ϕ16 mm bars will be employed for the main bars, and ϕ8mm bars for the stirrups (links)
d = 450 – 30 – 8 – 8 = 404 mm

k = M_Ed/(f_ckbd²) = (62.647 × 10⁶)/(35 × 300 × 404²) = 0.0365
Since k < 0.167, no compression reinforcement required
z = d[0.5+ √(0.25 – 0.882K) ] = z = d[0.5+ √(0.25 – 0.882(0.0365))] = 0.95d

A_s1 = M_Ed/(0.87f_yk z) = (62.647 × 10⁶)/(0.87 × 500 × 0.95 × 404) = 375.23 mm²
Provide 2H16 mm TOP (AS_prov = 402 mm²)

Interaction of shear and torsion
According to clause 6.3.2(2) of Eurocode 2, the effects of torsion and shear for both hollow and solid members may be superimposed, assuming the same value for the strut inclination θ. The limits for θ given in 6.2.3 (2) of EC2 are also fully applicable for the case of combined shear and torsion.

According to clause 6.3.2(4) of EC2, the maximum resistance of a member subjected to torsion and shear is limited by the capacity of the concrete struts. In order not to exceed this resistance the following condition should be satisfied:

T_Ed /T_Rd,max + V_Ed /V_Rd,max ≤ 1 ———- Equation (6.29 of EC2)

V_Ed = 157.7 KN
T_Ed = 4.819 kN.m
T_Rd,max = design torsional resistance moment
V_Rd,max = maximum shear resistance of the cross-section

Geometrical Properties for analysis of torsion
Area (A) = 300mm × 450mm = 135000 mm²
Perimeter (U) = 2(300) + 2(450) = 1500mm
Equivalent thickness = t_ef,i = A/U = 135000/1500 = 90mm

The equivalent thin wall section for the rectangular section is given below;

A_k= the area enclosed by the centre-lines of the connecting walls, including inner hollow areas = (450 – 90) × (300 – 90) = 75600 mm²
U_k= is the perimeter of the area A_k = 2(450 – 90) + 2(300 – 90) = 1140 mm

T_Rd,max = 2 v α_cwf_cdA_kt_ef,i sinθ cosθ

Assuming θ = 21.8° (cot θ = 2.5)
v = 0.6(1 – f_ck/250) = 0.6(1 – 35/250) = 0.516
f_cd = (α_cc × f_ck)/γ_c = (1 × 35)/1.5 = 23.33 N/mm²
T_Rd,max = 2 × 0.516 × 1.0 × 23.33 × 75600 × 90 × cos 21.8° × sin 21.8° × 10^-6 = 56.485 KNm

V_Rd,c = [C_Rd,c.k.(100ρ₁ f_ck)^(1/3) + k₁.σ_cp]b_w.d

Where;
C_Rd,c = 0.18/γ_c = 0.18/1.5 = 0.12
k = 1 + √(200/d) = 1 + √(200/404) = 1.704 > 2.0, therefore, k = 1.702
ρ₁ = As/bd = 402/(300 × 404) = 0.003317 < 0.02; K₁ = 0.15

V_Rd,c = [0.12 × 1.704(100 × 0.003317 × 35 )^(1/3)] 300 × 404 = 65469.358 N = 65.469 KN

Since V_Rd,c (65.469 KN) < V_Ed (157.7 KN), shear reinforcement is required.

The compression capacity of the compression strut (V_Rd,max) assuming θ = 21.8° (cot θ = 2.5)

V_Rd,max = (b_w.z.v₁.f_cd)/(cot⁡θ + tanθ)
V₁ = 0.6(1 – f_ck/250) = 0.6(1 – 35/250) = 0.516
f_cd = (α_cc ) f_ck)/γ_c = (1 × 35)/1.5 = 23.33 N/mm²
Let z = 0.9d

V_Rd,max = [(300 × 0.9 × 404 × 0.516 × 23.333)/(2.5 + 0.4)] × 10^-3 = 452.863 KN

Since V_Rd,c < V_Ed < V_Rd,max
Hence, A_sw/S = V_Ed/(0.87F_ykzcot θ) = 157700/(0.87 × 500 × 0.9 × 404 × 2.5 ) = 0.3988

Minimum shear reinforcement;
A_sw/S = ρ_w,min × b_w × sinα (α = 90° for vertical links)
ρ_w,min = (0.08 × √(f_ck))/f_yk = (0.08 × √35)/500 = 0.0009465
A_sw/S (min) = 0.0009465 × 300 × 1 = 0.2839
Since 0.2839 < 0.3988, adopt 0.3988

Maximum spacing of shear links = 0.75d = 0.75 × 404 = 303mm
Provide H8mm @ 250mm c/c (A_sw/S = 0.402) Ok

Note that this link must be properly closed with adequate anchorage length, because it will assist in resisting torsion.

Design Considerations for Torsion
T_Ed /T_Rd,max + V_Ed /V_Rd,max ≤ 1

(4.891/56.485) + (157.7/453.863) = 0.434 < 1.0 Hence it is ok

However, note that the actual shear force at the point where torsion is maximum is actually less than the shear force at the support. The relationship above is an error but on the safe side.

The maximum torsion occurs at an angle of 9.5° from the support (see Table above). Therefore, the actual shear force at that section ( V_Ed) = Shear force at support – wrα

V_Ed = 157.7 – (133.862 × 3 × (9.5/180) × π) = 91.114 KN

Therefore for educational purposes, this is the shear force that should be used to check the shear-torsion interaction. A little consideration will show that V_Rd,max is constant all through the section, but V_Rd,c might vary depending on the longitudinal reinforcement provided at the section.

Rechecking the interaction above;

(4.891/56.485) + (91.114/453.863) = 0.287< 1.0 Hence it is ok

Area of transverse reinforcement to resist torsion
A_sw/s = T_Ed/2A_k f_yw,d cotθ
A_sw/s = (4.819 × 10⁶) / (2 × 135000 × 0.87 × 500 × 2.5) = 0.0164 < A_sw/S (min)
Therefore, links provided for shear will be adequate for resisting torsion.

Area of longitudinal reinforcement to resist torsion
A_s1 = T_EdU_k cot θ / 2A_k f_yd
A_s1 = (4.819 × 10⁶ × 1140 × 2.5) / (2 × 75600 × 0.87 × 500) = 208 mm²

According to clause 6.3.2(4), in compressive chords, the longitudinal reinforcement may be reduced in proportion to the available compressive force. In tensile chords the longitudinal reinforcement for torsion should be added to the other reinforcement. The longitudinal reinforcement should generally be distributed over the length of side, but for smaller sections it may be concentrated at the ends of this length.

However, for the avoidance of doubt since no definition was given for what could be regarded as a ‘smaller section’, Provide 1H12mm bar at the middle of the section at both faces. The tensile and longitudinal reinforcement provided at the top and bottom of the section should be able to take care of the rest.

Further information
Nominal shear reinforcement is required in rectangular sections when;

T_Ed /T_Rd,c + V_Ed /V_Rd,c ≤ 1 ————– Equation (6.31 of EC2)

Where;
T_Rd,c is the value of the torsion cracking moment:
V_Rd,c is as defined above.

T_Rd,c = f_ctd⋅t⋅2A_k
τ = f_ctd = f_ctk /γ_c = 2.2/1.5 = 1.466 MPa (f_ctk deducted from Table [3.1 – EC2]).

It results therefore:
T_Rd,c = f_ctd⋅t⋅2A_k = 1.466 × 90 × 2 × 75600 × 10^-6 = 19.949 kNm

From above calculations;
V_Rd,c = [0.12 × 1.704(100 × 0.003317 × 35 )^(1/3)] 300 × 404 = 65469.358 N = 65.469 KN

(4.819/19.949) + 91.114/65.469) = 1.633 > 1.0 (Shear force at point of maximum torsion was used)

Therefore obviously this showed that shear reinforcement calculations were required.

References
Hassoun M.N., Al-Manaseer A. (2008): Structural Concrete Theory and Design (4th Edition). John Wile and Son Inc., New Jersey

Preparation of Bar Bending Schedule For Floor Slabs

By

Ubani Obinna Uzodimma

-

November 7, 2020

Bar bending schedule is an important structural working document that shows the disposition, bending shape, total length, and quantity of all the reinforcements that have been provided in a structural drawing. It is often provided in a separate sheet (usually A4 paper) from the structural drawing. The bar marks from structural detailing drawing are directly transferred to the bar bending schedule. We normally quantify reinforcements based on their total mass in tonnes or kilograms. For smaller projects, you can quantify based on the number of lengths needed.

Bar bending schedule is prepared for floor slabs to show the quantity, size, and shape of rebars needed during the construction. This document is very important for pre-contract and post-contract operations. The information needed for the preparation of bar bending schedule for floor slab is picked from the reinforcement detailing drawings. One important parameter in the preparation of bar bending schedule is the quantity of steel required (in kilograms or tonnes). This is based on the unit mass and size of the rebars.

Unit mass of rebars
The unit mass of the reinforcements are derived from the density of steel. The density of steel normally used for this purpose is 7850 kg/m³.

For example, let us consider 12mm bar;
The area is given by (πd²)/4 = (π × 12²)/4 = 113.097mm² = 0.0001131m²
Considering a unit length of the bar, we can verify that the volume of a metre length of the bar is 0.0001131m³;

Density = Mass/Volume = 7850 kg/m³ = Mass/0.0001131
Therefore, the unit mass of 12mm bar = 7850 × 0.0001131 = 0.888 kg/m

Therefore for any diameter of bar;
Basic weight = 0.00785 kg/mm² per metre
Weight per metre = 0.006165 ϕ² kg
Weight per mm² at spacing s(mm) = 6.165ϕ²/s kg

Where;
ϕ = diameter of bar in millimetres

The unit weight of different types of reinforcement sizes is given in the Table below;

Diameter of bar (mm)	Weight per metre (kg)	Length per tonne (m)
6	0.222	4505
8	0.395	2532
10	0.616	1623
12	0.888	1126
16	1.579	633
20	2.466	406
25	3.854	259
32	6.313	158
40	9.864	101

Basic Shapes for Bar Bending Schedule

There are some basic shape codes in the code of practice (BS 8666:2005). But these days, it is common to sketch the bending shape on the BBS document to avoid the confusion and extra effort that comes with extracting the shape from a standard document.

To obtain the length of reinforcement bars in a structural drawing, use the following relation;

Length of bar = Effective Length + Width of Support – Concrete cover (s) – Tolerances

The typical values of tolerances (deductions) are given in the table below;

Example on the Preparation of the Bar Bending Schedule of a Slab

To illustrate how this is done, consider the general arrangement of the first floor of a building as shown below;

Bar Bending Schedule Calculations

Cutting Length of reinforcement = A + B + C – r – 2d (Table 2.19, Reynolds, Steedman, and Threlfall, 2008)

Where;
r = radius of bend (r = 24 mm for high yield 12 mm bars; and 20 mm for Y10mm bars)
d = diameter of bar

Bar Mark 01:
A = 4000 + 230 – 35 = 4195 mm
B = 150 – 2(25) – 10 = 90 mm (including 10 mm tolerance)
C = 230 + 800 – 35 = 995 mm (from detailing considerations 0.2L)
r = 24 (for 12 mm bars)

L = A + B + C – r – 2d = 4195 + 90 + 995 – 24 – 2(12) = 5235 mm

Bar Mark 02:
L = 2230 mm

Bar Mark 03:
A = 3600 + 230 – 35 = 3795 mm
B = 150 – 2(25) – 12 – 10 = 78 mm (including 10 mm tolerance)
C = 230 + 720 – 35 = 915 mm (from detailing considerations 0.2L)
r = 24 (for 12 mm bars)

L = A + B + C – r – 2d = 3795 + 78 + 915 – 24 – 2(12) = 4740 mm

Bar Mark 04:
A = 1080 + 1200 + 230 – 25 = 2485 mm
B = 150 – 2(25) – 10 = 90 mm (including 10 mm tolerance)
C = 1200 + 230 – 25 = 1405 mm (from detailing considerations 0.2L)
r = 24 (for 12 mm bars)

L = A + B + C – r – 2d = 2485 + 1405 + 90 – 24 – 2(12) = 3932 mm

Bar Mark 05:
A = 6000 + 230 – 35 = 6195 mm
B = 150 – 2(25) – 12 – 10 = 78 mm (including 10 mm tolerance)
C = 1200 + 230 – 35 = 1395 mm (from detailing considerations 0.2L)
r = 20 (for 10 mm bars)

L = A + B + C – r – 2d = 6195 + 1395 + 78 – 20 – 2(10) = 7628 mm

Bar Mark 06:
L = 4630 mm

Bar Mark 07:

L = 3830 mm

Bar Mark 08:
A = 1200 + 230 – 35 – 25 – (15) = 1355 mm (including 15 mm tolerance)
B = 150 – 2(25) – 10 = 90 mm (including 10 mm tolerance)
r = 24 (for 12 mm bars)

L = 2(A) + 2(B) + C + D – 3r – 6d = 2(1355) + 2(90) + 2(125) – 3(24) – 6(12) = 2996 mm

Bar Mark 09:
L = 2030 mm

Bar Mark 10:
L = 1830 mm

The final table for the bar bending schedule can be prepared as shown below. However, it is important to include all details in the schedule to avoid confusion.

I hope you find this post helpful… Help tell others about Structville, and keep on visiting us.

Our Facebook fan page is at;
www.facebook.com/structville

How to Carry Out Concrete Mix Design

By

Ubani Obinna Uzodimma

-

May 25, 2021

Concrete mix design is the process of specifying and proportioning the quantity of concrete ingredients (cement, sand, gravel, and water) required to produce concrete with a specified fresh and hardened properties. Nowadays, engineers should have a deeper understanding of concrete mixes, than just specifying say 1:2:4 concrete mix ratio for their construction works.

Under normal and well-controlled conditions, 1:2:4 mix ratio should yield concrete with 28 days compressive strength greater than 20 N/mm². However, there are variations in results when batching by weight and when batching by volume. This situation demands that to produce concrete of a specified compressive strength, you have to accurately carry out concrete mix design, which incorporates the tendency of failure during tests.

A little consideration from concrete mix design results will show that the mix ratio for batching by weight, and for batching by volume are not basically the same for obtaining a specified grade of concrete.

Ingredients for concrete mix design — Figure 1: Basic ingredients for concrete production.

The compressive strength of concrete is a very variable quantity. Therefore, when carrying out a concrete mix design, it is important to target a higher average strength so that every part of the structure will meet the specified strength. Statistical standard deviation which is a measure of scatter or dispersion of strength about the mean is normally used to take care of this.

The target strength of concrete (f_m) during mix design is given by;

f_m = f_min + KSD ————– (1)

Where;

f_m is the mean compressive strength
f_min is the minimum compressive strength of the concrete. In the Eurocodes, this is called the characteristic strength of the concrete (f_ck), while in the US, it is called the design strength (f_c‘).
K is the probability factor which is usually taken as 1.64 or 2.33 to express the probability of 1 in 20 and 1 in 100 respectively, for the strength to fall below the minimum strength.
SD is the standard deviation which is best obtained by considering the previous test results obtained using the same materials, the same procedure, and under the same supervision.

The term KSD is normally referred to as the margin.

The probability of strength values in the range f_ck ± KSD and below f_ck – KSD (risk) for normal distribution is shown in Table 1.0 below;

Table 1: The probability of strength values in the range f_ck ± KSD and below f_ck – KSD (risk) for normal distribution (Neville and Brooks, 2010)

Probability factor (k)	Probability of strength values in the range f_ck ± KSD (%)	Probability of strength values below f_ck – KSD (%)
1.00	68.2	15.9 (1 in 6)
1.64	90.0	5.0 (1 in 20)
1.96	95.0	2.5 (1 in 40)
2.33	98.0	1.0 (1 in 100)
3.00	99.7	0.15 (1 in 700)

In the Eurocodes and in many other codes, the range of the risk of 1 in 20 is recommended for concrete tests. This means that in 20 concrete cubes, there is a probability of only one cube not meeting the required strength. When statistical data is not available for obtaining the standard deviation, the values in table 2 according to ACI code could be used.

Table 2: Required average compressive strength when data is not available to establish a standard deviation

Specified Compressive strength f’_c(MPa)	Required Average Compressive Strength f’_cr (MPa)
Less than 21	f’_c+ 7.0
21 to 35	f’_c+ 8.5
Over 35	1.10f’_c + 5

The process of carrying out concrete mix design are as follows;

Test the materials to be used for the concrete mix design. For the aggregates, it is important to obtain the oven-dry relative density, fineness modulus, absorption, and bulk density.
Establish the target strength of the concrete at 28 days by considering the characteristic strength and the margin which is based on the standard deviation.
Establish the required water-cement cement ratio for the target strength using relevant tables
Calculate the water requirement for the desired slump using relevant tables
Use the calculated water content to calculate the cement content using the water-cement ratio relationship
Calculate the mass of coarse aggregates using the bulk volume of coarse aggregate per unit volume of concrete
Calculate the mass of fine aggregates
Summarise your results

Worked Example

Let us consider the trial mix design for a concrete of minimum specified strength of 25 N/mm², to be employed in the construction of the floor beams and slab of a building.

Materials Analysis
Coarse aggregate: Crushed granite of nominal maximum size of 20mm
Oven dry relative density = 2.68
Fineness modulus = 2.60
Absorption = 0.4% (saturated surface dry)
Bulk density = 1650 kg/m³

Specific gravity of cement = 3.15

Fine aggregate: Sharp sand from river
Relative density = 2.64
Absorption = 0.60 %
Bulk density = 1600 kg/m³

The target strength can be obtained from the relation below;
f_m = f_ck + KSD
f_m = 25 + 8.5 = 33.5 N/mm²

Water-Cement Ratio

The relationship between the water to cement ratio for non-air-entrained concrete (normal concrete) and the 28 days compressive strength is given in Table 3.

Table 3: Relationship between compressive strength and water to cement ratio

Compressive strength at 28 days (MPa)	Water to cement ratio by mass
45	0.38
40	0.42
35	0.47
30	0.54
25	0.61
20	0.69
15	0.79

Therefore, Water – Cement ratio for non-air entrained 33.4 N/mm² concrete = 0.491 (interpolating from Table 3)

Cement and Water Content
Water content is normally estimated from workability requirements, which is guided by the slump. The range of slump required for different types of construction is given in Table 4;

Table 4: Different slumps for different types of construction works

Concrete Construction	Maximum slump (mm)	Minimum slump (mm)
Reinforced foundation walls and footings	75	25
Plain footings, caissons, and substructure walls	75	25
Beams and reinforced walls	100	25
Columns in buildings	100	25
Pavements and slabs	75	25
Mass cocrete	75	25

For maximum size of aggregate of 19mm, and a slump of 75mm, the Table 5 gives a water demand of 205 kg/m³

Table 5: Approximate mixing water and target air content requirements for different slumps and nominal maximum sizes of aggregate

Slump	Water content (kg/m³) for 9.5 mm aggregate size	Water content (kg/m³) for 12.5 mm aggregate size	Water content (kg/m³) for 19 mm aggregate size	Water content (kg/m³) for 25 mm aggregate size	Water content (kg/m³) for 37.5 mm aggregate size	Water content (kg/m³) for 50 mm aggregate size	Water content (kg/m³) for 75 mm aggregate size	Water content (kg/m³) for 150 mm aggregate size
25 – 50	207	199	190	179	166	154	130	113
75 – 100	228	216	205	193	181	169	145	124
150 -175	243	228	216	202	190	178	160	–
Approximate amount of entrapped air (%)	3	2.5	2	1.5	1	0.5	0.3	0.2

Therefore cement content;
205/C= 0.491; Therefore the cement content (C) = 205 / 0.491 = 417.515 kg/m³

Mass of Coarse Aggregates

For 19mm aggregate with a fineness modulus of 2.60, the bulk volume of dry rodded coarse aggregate per m³ of concrete is 0.64 (see Table 6).

Table 6: Bulk volume of coarse aggregate per unit volume of concrete

Nominal maximum size of aggregate (mm)	Bulk volume (2.40 fineness modulus)	Bulk volume (2.60 fineness modulus)	Bulk volume (2.80 fineness modulus)	Bulk volume (3.0 fineness modulus)
9.5	0.50	0.48	0.46	0.44
12.5	0.59	0.57	0.55	0.53
19	0.66	0.64	0.62	0.60
25	0.71	0.69	0.67	0.65
37.5	0.75	0.73	0.71	0.69
50	0.78	0.76	0.74	0.72
75	0.82	0.80	0.78	0.76
150	0.87	0.85	0.83	0.81

Therefore, mass of coarse aggregate (M_c) per m³ of concrete = 0.64 × 1650 = 1056 kg/m³
Approximate air content = 2%

Mass of fine aggregates
The mass of coarse aggregate can be estimated using the relationship below;

Mass of fine aggregate M_f = γ_f [1000 – (W – C/γ + Mc/γ_c + 10A)] ————- (2)

Where;
γ_f = Specific gravity of fine aggregate (saturated surface dry)
W = Mixing water requirement
C = Cement Content
γ = Specific gravity of cement (take value as 3.15 unless otherwise specified)
Mc = Coarse Aggregate content
γ_c = Specific gravity of coarse aggregate (saturated surface dry)
A = Air content (%)

Therefore:
M_f = 2.64 [1000 – (205 + (417.515/3.15) + (1056/2.68) + (10 × 2))] = 655.843 kg/m³

Final Volume computations
Water = 205 / (1 × 1000) = 0.205 m³
Cement = 417.515 / (3.15 × 1000) = 0.1325 m³
Air = 2/100 = 0.02
Coarse aggregate = 1056 / (2.68 × 1000) = 0.394 m³
Fine aggregate = 655.843 / (2.64 × 1000) = 0.248 m³

SUMMARY OF TRIAL MIX DESIGN
By weight
Water = 205 kg/m³
Cement = 417.515 kg/m³
Coarse Aggregate = 1056 kg/m³
Fine Aggregate = 655.843 kg/m³
Yield of concrete = 2334.36 kg/m³
Mix ratio by weight (Cement : Fine Aggregate : Coarse Aggregate) = (1:1.57:2.53)

By volume
Water = 0.205 m³
Cement = 0.1325 m³
Coarse Aggregate = 0.394 m³
Fine Aggregate = 0.248 m³

Mix ratio by volume (Cement : Fine Aggregate : Coarse Aggregate) = (1:1.87:2.97)

MIX DESIGN WITHOUT CONSIDERING TEST MARGIN
However, carrying out mix design for 25 N/mm² grade of concrete without considering the margin, we can obtain the following result using the steps described above;

Water-cement ratio
Water – Cement ratio for non-air entrained 25 N/mm² concrete = 0.61 (see Table 3 above)

Water and Cement Demand
For maximum size of aggregate of 19mm, and a slump of 75mm, gives a water demand of 205 kg/m³.
Therefore the cement content C = 205/0.61= 336.06 kg/m³

Mass of Coarse Aggregate
For 19mm aggregate with fineness modulus of 2.60, the bulk volume of dry rodded coarse aggregate per m³ of concrete is 0.64. Therefore;
Weight per m³ = 0.64 × 1650 = 1056 kg/m³

Approximate air content = 2%

Mass of Fine Aggregate
Mass of fine aggregate M_f = γ_f [1000 – (W – C/γ + Mc/γ_c + 10A)]
M_f = 2.64 [1000- (205 + (336.06/3.15) + (1056/2.68) + 10(2))] = 724.11 kg/m³

Volume computations
Water = 205 / (1 × 1000) = 0.205 m³
Cement = 336.06 / (3.15 × 1000) = 0.1066 m³
Air = 2/100 = 0.02%
Coarse aggregate = 1056 / (2.68 × 1000) = 0.394 m³
Fine aggregate = 724.11 / (2.64 × 1000) = 0.274 m³

Summary of trial mix design without considering the margin
By weight
Water = 205 kg/m³
Cement = 336.06 kg/m³
Coarse Aggregate = 1056 kg/m³
Fine Aggregate = 724.11 kg/m³
Yield of concrete = 2321.17 kg/m³
Mix ratio by weight (Cement:Fine Aggregate:Coarse Aggregate) = (1: 2.15: 3.142)

By volume
Water = 0.205 m³
Cement = 0.1066 m³
Coarse Aggregate = 0.394 m³
Fine Aggregate = 0.274 m³
Mix ratio by volume (Cement:Fine Aggregate:Coarse Aggregate) = (1:2.57:3.696)

Thank you for visiting Structville…….
We love you, and you can like our facebook fan page on;
www.facebook.com/structville

Design of Biaxial Reinforced Concrete Columns

By

Ubani Obinna Uzodimma

-

November 24, 2020

A biaxial column is a column that is subjected to compressive axial force and bending moment in the two planes. They are usually found at the corners of a building or at locations where the beam spans and/or loading are not equal. In the design of biaxial reinforced concrete columns, a non-linear analysis method is required, which should take into account second-order, imperfection, and biaxial bending effects.

Biaxial Reinforced Concrete Columns — The columns circled in red are biaxially loaded

EN 1992-1-:2004 (Eurocode 2) did not give an express method of designing biaxial columns other than working from the first principles. This may not be very easy to achieve without the use of charts or computer programs. To develop such a program, one can divide the compression zone into strips that are parallel with the neutral axis of the section, and calculate the stress in each strip using the parabolic-rectangular diagram. The force and moment at each strip in the x and y-axis can be summed up in the ultimate limit state to find the moment and axial force developed by the concrete in compression.

There are however simplified methods of dealing with biaxial bending in reinforced concrete structures. An example is the approach given in clause 5.8.9(4) of EN 1992-1-1 for the design of biaxially bent sections in slender columns. This is based on the observation that the form of the M_x – M_y interaction diagram can conveniently be represented by a super-ellipse. A super-ellipse has an equation of the form;

x^a + y^a = k —— (1)

If a = 2, this equation becomes a circle, while if a = 1 it describes a straight line. At loads approaching the squash load, the M_x – M_y interaction diagram approaches a circle, while in the region of the balance point it is close to a straight line. Clause 5.8.9(4) adopts the equation below as a means of describing the complete interaction surface;

(M_E,dz/M_R,dz )^a + (M_Ed,y/M_Rd,y )^a ≤ 1.0 —— (2)

The proximity to the squash load can be defined using the N/N_uz ratio parameter, and EN 1992-1-1 assumes the relationship between this parameter and the exponent ‘a‘ given in the Table below. Intermediate values may be interpolated.

N_Ed/N_Rd	0.1	0.7	1.0
a	1.0	1.5	2.0

In the Table above, N_Rd is the squash load of the column, and may be calculated from

N_Rd = A_cf_cd + A_sf_yd —— (3)

The difficulty with the approach from the practical point of view is that it cannot be used as a direct design method since N_Rd can only be established once the reinforcement area has been found. It, therefore, has to be used iteratively. An initial estimate is made of N/N_uz, the section is designed, a corrected value of N/N_uz can then be estimated, and the process repeated until a correct solution is obtained.

A much simpler, but considerably more approximate method to the design of biaxial columns has been adopted in BS 8110. The design is carried out for an increased uniaxial moment, which takes account of the biaxial effects. The required uniaxial moment is obtained from whichever is appropriate of the two relationships set out below:

if M_x/h’ > M_y/b’ then M’_x = M_x + βh’M_y/b’ —— (4)
if M_x/h’ < M_y/b’ then M’_y = M_y + βb’M_x /h’ —— (5)

In the above relationships, M_x and M_y are the design moments about the x and y axes, respectively, while M’_x and M’_y are the effective uniaxial moments for which the section is actually designed. b’ and h’ are the effective depths of the column section (see image below). The factor β is defined in BS 8110 as a function of N/bhf_cu. In terms of f_ck, it can be obtained from the relationship;

β = 1 – N/bhf_ck (0.3 < β < 1.0) —— (6)

BIAXIALLY%2BBENT%2BCOLUMN%2B%2528BS%2B8110%2529

This approach has the great advantage of being very simple. It is, however, an approximate approach.

Example on the Design of Biaxial Reinforced Concrete Columns to BS 8110 and Eurocode 2

A reinforced concrete column fixed at both ends is subjected to the loading condition shown below. We are required to obtain the appropriate longitudinal reinforcement for the column using BS 8110-1:1997 and Eurocode 2.

The column is carrying longitudinal and transverse beams of depth 600mm and width 300mm. It is also supported by beams of the same dimension. The centre to centre height of the column is 3500mm. The plan view of the arrangement of the beams and column is as shown below.

DESIGN ACCORDING TO BS 8110-1:1997
N = 716.88 kN;
TOP: M_x-x = 175.87 kNm; M_y-y = 35.52 kNm
BOTTOM: M_x-x= -85.832 kNm; M_y-y = -25.269 kNm

Concrete grade f_cu = 30 N/mm²
Yield Strength of reinforcement f_y = 460 N/mm²
Concrete cover = 40mm
L_o = 3.5m, Effective length L_e = 0.75 × (3500 – 600) = 2175 mm;
Size of column = 400 x 300mm;
Slenderness = 2175/300 = 7.25 < 15. Thus column is short.

Effective depth about x-x axis
h’ = (400 – 40 – 12.5 – 10) = 337.5 mm

Effective depth about y-y axis
b’ = (300 – 40 – 12.5 – 10) = 237.5 mm

M_x/h’ = 521.109 kN; M_y/ b’ = 149.558 kN

Axial-load ratio
N_ratio = (N × 1000) / (F_cu × b × h) = (716.88 × 1000) / (30 × 400 × 300) = 0.1991

From Table 3.22 of BS 8110-1:1997, for N_ratio = 0.1991
Therefore, β = 1 – 1.1644(0.1991) = 0.7681

As M_x/h’ exceeds M_y/b’
M_x‘ = M_x + βh’/b’M_y
M_x‘ = 175.87 + [0.7681 × (0.3375)/(0.2375 ) × 35.52] = 214.64 kNm

Minimum Eccentricity in Columns
According to clause 3.8.2.4 of BS 8110-1:1997, at no section in a column should the design moment be taken as less than that produced by considering the design ultimate axial load as acting at a minimum eccentricity, e_min equal to 0.05 times the overall dimension of the column in the plane of bending considered but not more than 20 mm.

Where biaxial bending is considered, it is only necessary to ensure that the eccentricity exceeds the minimum about one axis at a time.

In the x-x direction = e_min = 0.05 × 400 = 20mm, therefore adopt 20mm, M_x = 716.88 × 0.02 = 14.3376 kNm < 214.64 kNm

In the y-y direction = e_min = 0.05 × 300 = 15mm, therefore adopt 15mm, M_y = 716.88 × 0.015 = 10.7532 kNm < 214.64 kNm

Section design ratios for chart entry
Axial load ratio N_ratio = (N × 1000)/(F_cu × b × h) = (716.88 × 1000)/(30 × 400 × 300) = 0.1991

M_ratio = M/(F_cu × b × h²) = (214.64 × 10⁶) / (30 × 300 × 400²) = 0.149

With d’/h = 337.5/400 = 0.84375

From chart, (ρ × F_y)/(F_cu) = 0.286 Therefore, ρ = (0.286 × 30) / 460 = 0.01865
A_SCreq = 0.01865 × 400 × 300 = 2238.26 mm²

Provide 6Y25mm (A_sprov = 2946 mm²)
Maximum area of reinforcement = 0.06bh = 0.06 × 400 × 300 = 7200 mm²

DESIGN ACCORDING TO EUROCODE 2
Clause 5.8.9(2) of EN 1992-1-1:2004 permits us to perform separate designs in each principal direction, disregarding biaxial bending as a first step. Imperfections need to be taken into account only in the direction where they will have the most unfavourable effect. However, in this example, we have carried out imperfection analysis in both directions.

N_Ed = 716.88 KN

Elastic Moments
Y – direction: M₀₁ = 175.87 kNm; M₀₂ = -85.832 kNm
Z – direction: M₀₁ = 35.52 kNm; M₀₂ = -25.269 kNm

Clear column height (L) = 3500 – 600 = 2900 mm

Calculation of the effective height of the column (L_o)
Let us first of all calculate the relative stiffnesses of the members in the planes of bending.

In the y-direction;
Second moment of area of beam 1 (I₁) = bh³/12 = 0.3 × 0.6³/12 = 0.0054 m⁴
Stiffness of beam 1 (since E is constant) = 4I₁/L = (4 × 0.0054) / 6 = 0.0036

Second moment of area of beam (I₂) = bh³/12 = 0.3 × 0.6³/12 = 0.0054 m⁴
Stiffness of beam 2 (since E is constant) = 4I₂/L = (4 × 0.0054) / 3.5 = 0.00617

Second moment of area of column (I_c) = bh³/12 = 0.0016 m⁴
Stiffness of column = 4I_c/L = (4 × 0.0016) / 3.5 = 0.001828

For compression members in regular braced frames, the slenderness criterion should be checked with an effective length l₀ determined in the following way:

L_o = 0.5L √[(1 + k₁)/(0.45 + k₁)) × (1 + k₂)/(0.45 + k₂))]

Where;
k₁, k₂ are the relative flexibilities of rotational restraints at ends 1 and 2 respectively
L is the clear height of the column between the end restraints

k = 0 is the theoretical limit for rigid rotational restraint, and k = ∞ represents the limit for no restraint at all. Since fully rigid restraint is rare in practise, a minimum value of 0.1 is recommended for k₁ and k₂.

In the above equations, k₁ and k₂ are the relative flexibilities of rotational restraint at nodes 1 and 2 respectively. If the stiffness of adjacent columns does not vary significantly (say, the difference not exceeding 15% of the higher value), the relative flexibility may be taken as the stiffness of the column under consideration divided by the sum of the stiffness of the beams (or, for an end column, the stiffness of the beam) attached to the column in the appropriate plane of bending.

Remember that we will have to reduce the stiffness of the beams by half to account for cracking;

k₁ = k₂ = 0.001828 / (0.0018 + 0.003085) = 0.3743

L_o = 0.5 × 2900√[((1 + 0.3743)/(0.45 + 0.3743)) × (1 + 0.3743)/(0.45 + 0.3743)] = 2647.77 mm

Compare with BS 8110’s 0.75L = 0.75 × 2900 = 2175 mm

In the z-direction;
Second moment of area of beam 3 (I₃) = bh³/12 = 0.3 × 0.6³/12 = 0.0054 m⁴
Stiffness of beam 3 (since E is constant) = 4I₁/L = (4 × 0.0054) / 3.5 = 0.00617

Second moment of area of column (I_c) = bh³/12 = 0.0009 m⁴
Stiffness of column = 4I_c/L = (4 × 0.0009) / 3.5 = 0.00102857

k₁ = k₂ = 0.00102857/(0.003085) = 0.3334

l_o = 0.5 × 2900 √[(1 + 0.3334) / (0.45 + 0.3334) × (1 + 0.3334) / (0.45 + 0.3334)] = 2675.293 mm

Radius of gyration

i_x = h/√12 = 400/√12 = 115.47
i_z = b/√12 = 300/√12 = 86.602

Slenderness in the x-direction (λ_x) = 2647.77/115.47 = 22.930
Slenderness in the z-direction (λz) = 2675.293/86.602 = 30.892

Critical Slenderness for the y-direction
λ_lim = (20.A.B.C)/√n
A = 0.7
B = 1.1
C = 1.7 – M₀₁/M₀₂ = 1.7 – [(-85.832)/175.87] = 2.188
n = N_Ed / (A_c f_cd)
N_Ed = 716.88 × 10³ N
A_c= 400 × 300 = 120000 mm²
f_cd = (α_cc f_ck)/1.5 = (0.85 × 30)/1.5 = 17 N/mm²
n = (716.88 × 10³) / (120000 × 17) = 0.3514
λ_lim = (20 × 0.7 × 1.1 × 2.188 )/√0.3514 = 56.842

22.930 < 56.842, second order effects need not to be considered in the y-direction

Critical Slenderness for the z-direction
A = 0.7
B = 1.1
C = 1.7 – M₀₁/M₀₂ = 1.7 – [(-25.269)/35.52] = 2.411
n = N_Ed / (A_c f_cd)
N_Ed = 716.88 × 10³ N
Ac = 400 × 300 = 120000 mm²
fcd = (α_cc f_ck)/1.5 = (0.85 × 30)/1.5 = 17 N/mm²
n = (716.88 × 10³) / (120000 × 17) = 0.3514

λ_lim = (20 × 0.7 × 1.1 × 2.411 )/√0.3514 = 62.634

30.892 < 62.634, second-order effects need not be considered in the z-direction

Design Moments (y-direction)

Y – direction: M₀₁ = 175.87 kNm; M₀₂ = -85.832 kNm

e₁ is the geometric imperfection = (θ_i l₀/2) = (1/200) × (2647.77/2) = 6.619 mm

Minimum eccentricity e₀ = h/30 = 400/30 = 13.333 mm. Since this is less than 20mm, take minimum eccentricity = 20mm (clause 6.1(4) EC2).

Minimum design moment = e₀N_Ed = 20 × 10^-3 × 716.88 = 14.3376 kNm

First order end moment M₀₂ = M_Top + e_iN_Ed
e_iN_Ed = 6.619 × 10^-3 × 716.88 = 4.745 KNm
M₀₂ = M_Top + e_iN_Ed = 175.87 + 4.754 = 180.624 KNm

Longitudinal Steel Area
d₂ = C_nom + ϕ/2 + ϕ_links = 40 + 12.5 + 10 = 62.5 mm

d₂/h = 62.5/400 = 0.156
Let us read from chart; d₂/h = 0.15;

M_Ed/(f_ck bh²) = (180.624 × 10⁶)/(30 × 300 × 400² ) = 0.125
N_Ed/(f_ck bh) = (716.88 × 10³) / (30 × 300 × 400) = 0.199

From the chart, (A_s F_yk)/(bhf_ck) = 0.23

Area of longitudinal steel required A_s,req = (0.23 × 30 × 400 × 300)/460 = 1800 mm²

A_s,min = 0.10 N_Ed/f_yd = (0.1 × 716.88)/400 = 0.179 mm² < 0.002 × 400 × 300 = 240 mm²
A_s,max = 0.04bh = 4800 mm²
Provide 4Y25mm (Asprov = 1964 mm²)

Design Moments (z-direction)z – direction: M₀₁ = 35.52 kNm; M₀₂ = -25.269 kNm

e₁ is the geometric imperfection = (θ_i l₀/2) = (1/200) × (2675.293/2) = 6.688 mm

Minimum eccentricity e₀ = h/30 = 400/30 = 13.333 mm. Since this is less than 20mm, take minimum eccentricity = 20mm (clause 6.1(4) EC2)

Minimum design moment = e₀N_Ed = 20 × 10^-3 × 716.88 = 14.3376 kNm

First order end moment M₀₂ = M_Top + e_iN_Ed
e_iN_Ed = 6.688 × 10^-3 × 716.88 = 4.794 KNm
M₀₂ = M_Top + e_iN_Ed = 35.52 + 4.794 = 40.314 KNm

Longitudinal Steel Area
d₂ = C_nom + ϕ/2 + ϕ_links = 40 + 12.5 + 10 = 62.5 mm
d₂/h = 62.5/400 = 0.156

Reading from chart No 1; d₂/h = 0.156;
M_Ed/(f_ck bh²) = (40.314 × 10⁶)/(30 × 300 × 400²) = 0.0279
N_Ed/(f_ck bh) = (716.88 × 10³) / (30 × 300 × 400) = 0.199

From the chart, (A_s F_yk)/(bhf_ck) = 0.00 (Nominal reinforcement required)

Biaxial Effects

Check if λ_y / λ_z ≤ 2.0 and λ_z/λ_y ≤ 2.0

17.203/18.159 = 0.9473 < 2.0, and 18.159/17.203 = 1.0556 < 2.0

Furthermore, let us also check;
(e_y/h_eq) / (e_z/b_eq) ≤ 0.2 or (e_z / b_eq) / (e_y / h_eq) ≤ 0.2

The definition of eccentricity is given in Figure 5.8 of EC2

e_y = M_Ed,y/N_Ed = (180.624 × 10⁶) / (716.88 × 10³) = 251.958 mm
e_z = M_Ed,z/N_Ed = (40.314 × 10⁶) / (716.88 × 10³) = 56.235 mm

h_eq = i_z.√12 = 300 mm
b_eq = i_y.√12 = 400 mm

(e_y/h_eq) ÷ (e_z/b_eq) = 251.958/300 ÷ 56.235/400 = 5.9739 > 0.2

Therefore we have to check for biaxial bending interaction;

(M_E,dz/M_R,dz )^a + (M_Ed,y/M_Rd,y )^a ≤ 1.0

(A_s F_yk)/(bhf_ck) = (1964 × 460) / (30 × 300 × 400) = 0.251

Therefore from the chart; M_Rd/(f_ckbh²) = 0.13

M_Rd = (0.13 × 30 × 300 × 400²) × 10^-6 = 187.2 KNm

N_Rd = A_cf_cd + A_sf_yd
N_Rd = [(300 × 400 × 17) + (1964 × 400)] × 10^-3 = 2825.6 kN
N_Ed/N_Rd = 716.88 / 2825.6 = 0.2537

To evaluate the value of a, let us look at the table below as given in Clause 5.8.9(4) of EC2

By linear interpolation, a = 1.0 + [(0.2537 – 0.1 )/(0.7 – 0.1)] × (1.5 – 1.0) = 1.128

(M_E,dz/M_R,dz )^a + (M_Ed,y/M_Rd,y )^a ≤ 1.0

(40.314/187.2)^1.128 + (180.624/187.2)^1.128 = 0.1769 + 0.9606 = 1.1375 > 1.0.
This is not ok, and this shows that 4Y25 is inadequate for the biaxial action on the column.

Let us increase the area of steel to 6Y25mm (A_sprov = 2946 mm²)

Let us check again;
(A_s F_yk)/(bhf_ck) = (2964 × 460) / (30 × 300 × 400) = 0.3787
Therefore from the chart; M_Rd/(f_ckbh²) = 0.175
M_Rd = (0.175 × 30 × 300 × 400²) × 10^-6 = 252 kNm

N_Rd = A_cf_cd + A_sf_yd
N_Rd = [(300 × 400 × 17) + (2964 × 400)] × 10^-3 = 3225.6 kN

N_Ed/N_Rd = 716.88 / 3225.6 = 0.222

By linear interpolation, a = 1.0 + [(0.222 – 0.1 )/(0.7 – 0.1)] × (1.5 – 1.0) = 1.102

(M_E,dz/M_R,dz )^a + (M_Ed,y/M_Rd,y )^a ≤ 1.0

(40.314/252)^1.102 + (180.624/252)^1.102 = 0.132 + 0.6928 = 0.825 > 1.0.

This shows that 6Y25mm is adequate for the column, and shows some agreement with result from BS 8110-1:1997.

Thank you for visiting Structville

Visit our facebook fan page;
www.facebook.com/structville

How to Estimate the Cost of Tiling a 3 Bedrooms Flat

By

Ubani Obinna Uzodimma

-

January 6, 2022

Using tiles to cover the surfaces of floors, walls, countertops, etc can be a very attractive option for finishes in a building. Tiles can provide hard, durable, and aesthetically pleasing surfaces in a building provided that the tiling job is properly done. There are some basic principles that must be followed in order to achieve quality, beautiful and durable tiling.

For a homeowner and/or contractor, cost is a major factor that influences the decision and quality of tiling to be done. The basic factor that can influence the final cost of tiling a house are;

Cost of the tiles
Cost of screeding
Cost of adhesives
Cost of grouting cement
Cost of tiling accessories such as edge trimmers
Cost of labour
Size of area to be tiled

In this article, we are going to show how to estimate the cost of tiling a house in Nigeria using a three bedrooms apartment as an example. The floor plan of the three bedrooms apartment is shown in Figure 1. It is desirous to tile all the floors of the building according to the following specifications;

(1) All bedrooms, kitchen, and rear balcony/sit-out: 40cm × 40cm made in Nigeria ceramic tiles

(2) The sitting room, dining, and front balcony/sit-out: (30cm × 60cm) imported Virony glazed tiles;

(3) All the toilets and bathrooms: (30cm × 30cm) made in Nigeria ceramic tiles.

We are required to estimate the total cost of tiling the entire floor of the building, considering materials and labour.

FLOOR%2BPLAN — **Figure 1:** Floor plan of a three bedrooms apartment

Material Prices (informative)

It is very important for you to make an adequate market survey, in order to know the exact prices of materials in your area. This is the only chance you have of making a reasonably accurate estimate. The prices stated below are a bit representative, but merely informative. Note that tiles with designs may be more expensive than plain tiles or tiles with a single colour.

(40cm × 40cm) Ceramics Tiles = ₦3,360 per carton (12 pieces per carton – 1.92 square metre)

(30cm × 60cm) Porcelain Glazed Tiles = ₦5,760 per carton (8 pieces per carton – 1.44 square metre)

(30cm × 30cm) Ceramic Tiles = ₦2,700 per carton (17 pieces per carton – 1.53 square metre)

1 tonne of sand = ₦4,000

1 bag of cement = ₦4,000
5 kg of white cement = ₦2,500
Water seal = ₦700 per kg
Tile gum (20kg) = ₦1,450

BILL NO 1: TILES AND TILING ACCESSORIES
(a) Tiling of the bedrooms, kitchen, backyard sit-out, and store with (40cm × 40cm) Time Ceramics Tiles

We have to calculate the floor areas where we are going to apply the (40cm × 40cm) tiles;

Bedroom 1 = (3.6m × 3.45m) = 12.42 m²
Bedroom 2 = (3.6m × 3.6m) = 12.96 m²
Bedroom 3 = (3.15m × 3.17m) = 9.9855 m²
Kitchen = [(3.35m × 2.35m) + (1.37m × 1.075m)] = 9.34525 m²
Store = (2.025m × 1.775m) = 3.59 m²
Kitchen Sit-out = (1.37m × 2.075m) = 2.84275 m²
Total Area = 51.148 m²
Area of a piece of tile = (0.4m × 0.4m) = 0.16 m²

The number of pieces of tiles required to complete the floor areas = 51.148/0.16 = 319.675 pcs

Therefore, the number of cartons required = 319.675/12 = 26.639 cartons.

We will therefore provide 30 cartons of (40cm × 40cm) ceramic tiles. Extra tiles will account for damages, and for skirting of the foot of the walls.

Therefore the cost of the (40cm x 40cm) tiles = 30 × ₦3,360 = ₦100,800

(b) Tiling of the sitting room, dining, and entrance porch with (60cm x 30cm) tiles
The floor areas where we are going to apply the (60cm × 30cm) tiles;

Sitting room = (5.65m × 4.625m) = 26.13125 m²
Dining = (2.35m × 3.35m) = 7.8725 m²
Entrance Porch = (3.78m × 1.475m) = 5.5755 m²
Total Area = 39.579 m²
Area of a piece of tile = (0.6m × 0.3m) = 0.18 m²

The number of pieces of tiles required to complete the floor areas = 39.579/0.18 = 219.883 pcs;

Therefore, the number of cartons required = 219.883/8 = 27.485 cartons

We will therefore also provide 30 cartons of (60cm × 30cm) ceramic tiles.

Therefore the cost of the (60cm x 30cm) tiles = 30 × ₦5,760 = ₦172,800

(c) Tiling of the bathroom and toilet floors with (30cm x 30cm) tiles
On calculating the floor areas where we going to apply the (30cm × 30cm) tiles;

Bathroom and Toilet 1 and 2 = 2(2.0m × 1.1m) = 4.4 m²
Bathroom and toilet 3 = (2.0m × 0.985m) = 1.97 m²
Visitor’s toilet = (2.0m × 0.875m) = 1.75 m²
Total Area = 8.12 m²
Area of a piece of tile = (0.3m × 0.3m) = 0.09 m²

The number of pieces of tiles required to complete the floor areas = 8.12/0.09 = 90.222 pcs

Therefore, the number of cartons required = 90.222/17 = 5.307 cartons

We will therefore provide 7 cartons of (30cm × 30cm) ceramic tiles

Therefore the cost of the (30cm x 30cm) tiles = 7 × ₦2,700 = ₦18,900

(d) Loading, transportation, and offloading at the site (say) = ₦20,000

Therefore, sub-total 1 = ₦100,800 + ₦172,800 + ₦18,900 + ₦20,000 = ₦312,500

BILL NO 2: CEMENT AND SAND
We are going to make 25mm thick screeding to receive the tiles.

From above, you can verify that the total floor area of the building = 51.148 m²+ 39.579 m²+ 8.12 m²= 98.847 m²

Volume of mortar required = 98.847 × 0.025 = 2.471 m³
Using a mix ratio of 1:5

Cement required = 6 bags/m³
Sand required = 1800 kg/m³

Cement required = 14.826 bags (provide 15 bags)
Sand required = 4.447 tonnes (provide 5 tonnes)

Alternative calculation by site experience
From experience, 2 bags of cement is sufficient to complete the entire tiling process of (3.6m × 3.6m) room

Therefore;
2 bags of cement = 12.96 m²
x bags of cement = 98.847 m²

On solving;
x = 15.254 bags of cement; say 16 bags of cement

From experience, about 20 – 22 head pans of sharp sand is sufficient to complete the entire screeding process of (3.6m × 3.6m) room;

22 head pans = 22 × 0.0175 m³= 0.385 m³

Therefore;
0.385 m³ of sand = 12.96 m²
x m³ of sand = 98.847 m²

On solving;
x = 2.936 m³ sand = 4.844 tonnes of sand

Therefore, provide;

5 tonnes of sharp sand = ₦20,000
The cost of cement = 16 × ₦4,000 = ₦64,600
Water seal = 16 packs = 16 × ₦700 = ₦11,200
Tile gum = 17 bags × ₦1450 = ₦24,650
Other tiling accessories (allow) = ₦20,000
Transportation (say) = ₦5,000

Sub total 2 = ₦145,450

BILL NO 3: LABOUR
Cost of tiling 1m²of floor = ₦500

Therefore;
1 m² = ₦350
98.847 m² = x

On solving;
x = ₦49,423 (rounding up to the nearest 100)

Therefore, cost of labour = ₦50,000

GRAND TOTAL = ₦ 312,500 + ₦145,450 + ₦50,000 = ₦507,950

Therefore the cost of tiling the floor of the building = ₦507,950 + VAT + Engineer’s/Architect’s Profits

Thank you for reading

Like our facebook page;
www.facebook.com/structville

Free Vibration of Trusses: A solved Example

By

Ubani Obinna Uzodimma

-

November 2, 2022

Dynamics of structures is a special branch of structural analysis, which deals with the behaviour of structures subjected to dynamic loads (loads that vary with time). Such loads develop dynamic reactions, internal forces, and displacements in the structure. These values all change with time, and maximum values often exceed static load reaction values. Dynamic analysis of any structure often begins with free vibration analysis.

A structure undergoes free vibration when it is brought out of static equilibrium and can then oscillate without any external dynamic excitation. Free vibration of structures occurs with some frequencies which depend only on the parameters of the structures such as boundary conditions, distribution of masses, stiffnesses within the members etc, and not on the reason for the vibration.

At each natural frequency of free vibration, the structure vibrates in simple harmonic motion where the displaced shape (mode shape) of the structure is constant but the amplitude of the displacement varies in a sinusoidal manner with time. The number of natural frequencies in a structure coincides with the number of degrees of freedom in the structure. These frequencies are inherent to the given structure and are often referred to as eigenfrequencies. Each mode shape of vibration shows the form of an elastic curve which corresponds to a specific frequency.

Read also…
Deflection of trusses

Worked Example

A truss is loaded as shown below with a lumped mass of 5000 kg. We are to obtain the eigenfrequencies and mode shapes by assuming linear behaviour, neglecting damping, and assuming that the stiffness and inertial effects are time-independent.

E = 205 kN/mm²
Cross-sectional area = 0.00548 m² (UB 254 x 146 x 43)

A little consideration will show that the structure has two degrees of freedom which are given by the vertical and horizontal translation at node C. The lumped mass at the node will definitely participate in those movements. The displacements are given by Y₁ and Y₂ below.

Geometrical Properties
θ = tan^-1(3/4) = 36.869°
cos θ = 0.8
sin θ = 0.6
L_AC = √(3² + 4²) = 5m

γ = tan^-1(4/4) = 45°
cos γ = 0.7071
sin γ = 0.7071
L_BC = √(3² + 3²) = 4.243m

ANALYSIS OF STATE 1; Y₁ = 1.0

∑F_y = 0
-0.6F_AC – 0.7071F_CB = 1.0 ———– (1)

∑F_x = 0
-0.8F_AC + 0.7071F_CB = 0 ———– (2)

Solving (1) and (2) simultaneously
F_AC = -0.7143
F_CB = -0.8081

ANALYSIS OF STATE 2; Y₂ = 1.0

∑F_y = 0
-0.6F_AC – 0.7071F_CB = 0 ———– (3)

∑F_x = 0
-0.8F_AC + 0.7071F_CB = -1.0 ———– (4)

Solving (3) and (4) simultaneously
F_AC = 0.7143
F_CB = -0.6061

The frequency equation of a 2 degree of freedom system in terms of displacement is given by;

frequency%2Bequation%2Bin%2Bterms%2Bof%2Bdisplacement

Where;
M is the lumped mass
A is the amplitudes (Note that the system does not allow us to find the amplitudes but we can find the ratio of the amplitudes)
ω is the angular velocity
δ_ijis the axial displacement given by;

For the system above, we can easily compute this;

δ₁₁ = 1/EA[(-0.7143 × -0.7143 × 5) + (-0.8081 × -0.8081 × 4.243)] = 5.3219/EA
δ₂₂ = 1/EA[(0.7143 × 0.7143 × 5) + (-0.6061 × -0.6061 × 4.243)] = 4.1098/EA
δ₂₁ = δ₁₂ = 1/EA[(-0.7143 × 0.7143 × 5) + (-0.6011 × -0.8081 × 4.243)] = -0.4729/EA

To simplify our calculations, let δ₀ = 1/EA
Also let λ = 1/Mδ₀ω²
Therefore;

(5.3219 – λ)A₁ – 0.4729A₂ = 0
0.4729A₁ + (4.1098 – λ)A₂ = 0

On expanding;
λ² – 9.4317λ + 21.6484 = 0

On solving the quadratic equation;
λ₁ = 5.4845
λ₂ = 3.9472

You can verify that ω² = EA/λM

Therefore;
ω₁² = (0.1823 × 205 × 10⁶ × 0.00548)/5000 = 40.959
ω₂² = (0.2533 × 205 × 10⁶ × 0.00548)/5000 = 56.911

Hence;
ω₁= 6.399 rad/s
ω₂= 7.544 rad/s

To obtain the mode shapes;

For the first mode of vibration; Let A₁ = 1.0
(5.3219 – λ)A₁ – 0.4729A₂ = 0
(5.3219 – 5.4845) – 0.4729 A₂ = 0
Therefore, A₂ = -0.1626/0.4729 = -0.344
Φ₁ = [1.000 -0.344]^T

For the second mode of vibration; Let A₁ = 1.0
(5.3219 – λ)A₁ – 0.4729A₂ = 0
(5.3219 – 3.9472) – 0.4729 A₂ = 0
Therefore, A₂ = 1.3737/0.4729 = 2.9069
Φ₂ = [1.000 2.907]^T

The modal matrix is then defined as;

Free Vibration of Trusses: A solved Example 90

Remember Structville….
We have an interesting Facebook interactive page
Visit us at www.facebook.com/structville

Understanding Sign Conventions in Structural Analysis

By

Ubani Obinna Uzodimma

-

December 17, 2022

Table of Contents

Understanding sign conventions is one of the most important aspects of structural analysis. As a matter of fact, it is always a pausing point for all civil engineering students being introduced to structural analysis for the first time. If you do not understand sign conventions properly, it will be difficult to make significant progress in mastering structural analysis calculations.

The three most prominent internal forces in structural analysis calculations are the bending moment, shear force, and axial force. It is very common for people to define and state their sign convention before proceeding with any structural analysis problem. This is mainly due to variations in the selection of positive and negative coordinates.

For instance, most Indian and American textbooks will adopt the conventional cartesian coordinates system, and plot all positive bending moment upwards, and negative moments downwards, while most British and Scandinavian textbooks will plot positive moment downwards, and negative moments upwards.

However, it is important to note that what matters most in sign conventions is consistency. You must be consistent with whatever sign convention you choose to adopt, otherwise, errors will come in. If properly done, the values will remain the same, but the signs will differ.

Is there any standard approach?

I will prefer to answer yes because it is more appropriate to plot the bending moment diagram in the tension zone/fibre/face of a structural member. This is especially important in reinforced concrete structures where there is a need to provide tension reinforcement.

For instance, if you consider a continuous beam subjected to uniformly distributed load with the bending moment diagram plotted in the tension zone, you can easily point out and provide bottom reinforcements at the spans, and top reinforcements at the supports.

See an example below;

BENDING%2BMOMENT%2BPLOT — Consistency of bending moment diagram with the arrangement of reinforcements

From the figure above, you can see the consistency of the bending moment diagram with the typical arrangement of the reinforcement. This is because the bending moment diagrams were plotted in the tension zone, and of course, it means that the positive moment was plotted downwards. However, if the cartesian coordinates system was strictly followed, we would have been reversing the placement of the reinforcements with the bending moment diagram.

The same thing also applies to frames. You should plot your bending moment diagram in the tension zone of the members of the frame.

However, there are procedures that you must follow in your calculations in order to be consistent. By consistent, what I mean is that your positive bending moment will imply a sagging moment, while negative will mean a hogging moment. With this, you can plot your diagram directly as you have calculated, without having to interchange signs.

The summary of the procedures is given below.

Sign Convention for Beams

Bending moment

When you are coming from the left-hand side of the structure, all clockwise moments are positive and vice versa. When you are coming from the right-hand side of the structure, all anti-clockwise moments are positive and vice versa.

Shear force

When you are coming from the left, upward forces are positive, while downward forces are negative. When you are coming from the right, downward forces are positive, while upward forces are negative.

Axial force

Compressive axial forces are negative, while tensile axial forces are positive.

Understanding Sign Conventions in Structural Analysis 103

All you have to do is to look at the direction of the force. When coming from the left-hand side of beams, axial forces pointing towards the right means that the beam/section is in compression. When coming from the right, axial forces pointing towards the right means that the beam/section is in tension and vice versa

Sign Convention for Frames

For the sign of convention of frames, we are going to use the frame below as an example.

Bending moment

When coming from the left-hand side, all clockwise moments are positive, and anti-clockwise moments negative. All you have to do is to look at the point where you are taking your moment and observe the nature of rotation the force will produce. This is valid for both vertical and horizontal forces.

When coming from the right, all anti-clockwise moments are positive.

For frames, we plot positive moments inside, and negative moments outside the frame. See the example below.

Shear force

When coming from the left, upward vertical forces are positive and downward forces are negative. For horizontal forces on columns, forces pointing towards the right produce negative shear forces.

When coming from the right, downward vertical forces are positive, while upward vertical forces are negative. Horizontal forces on columns pointing towards the left will produce positive shear forces.

We plot positive shear forces outside the frame, and negative shear forces inside the frame.

Axial Force

When coming from the bottom of columns, upward vertical support reactions means that the column is in compression whether you are coming from the left or right.

When coming from the right-hand side of beams, forces pointing towards the right means that the beam is in compression and vice versa.

To me, you are free to select any location to plot your axial forces. Some people draw axial force diagrams to coincide with the centerline of the structure. In the classroom where I was trained, we draw negative axial forces outside the frame, and positive axial forces inside the frame. So it’s your choice to make.

Understanding Sign Conventions in Structural Analysis 107

I hope you find this article useful. If so, I will like you to share it.

Continue to visit Structville and tell your colleagues about us.

Our facebook page is at
www.facebook.com/structville

Worked Example

Geotechnical Design

Wall Pressure Calculations

Resistance to Sliding

Resistance to Overturning

Bearing Capacity Check

Structural Design

Design of the Wall

Design of the Base

Basic Shapes for Bar Bending Schedule

Example on the Preparation of the Bar Bending Schedule of a Slab

Worked Example

Example on the Design of Biaxial Reinforced Concrete Columns to BS 8110 and Eurocode 2

Material Prices (informative)

Worked Example

Is there any standard approach?

Sign Convention for Beams

Bending moment

Shear force

Axial force

Sign Convention for Frames

Bending moment

Shear force

Axial Force

EDITOR PICKS

POPULAR POSTS

POPULAR CATEGORY

ABOUT US

FOLLOW US