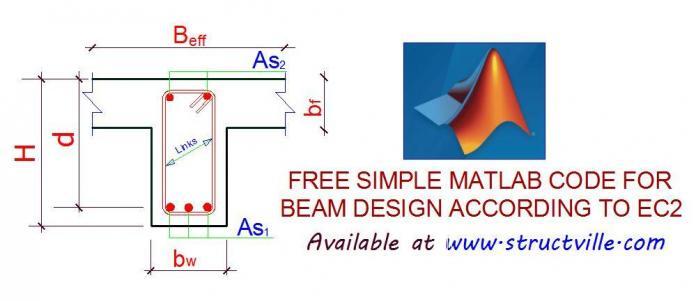
Free MATLAB Code for Flexural Design of R.C. Sections According to EC2

By

-

February 13, 2020

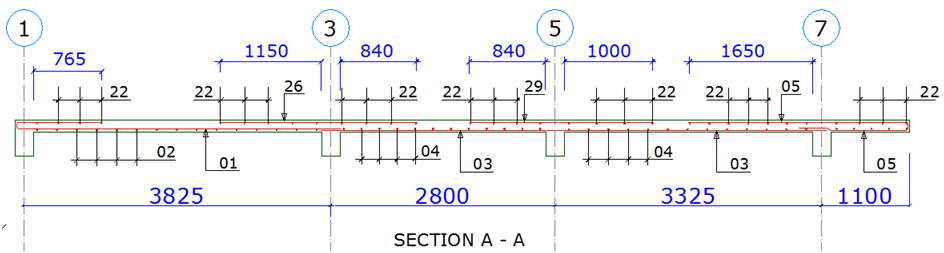
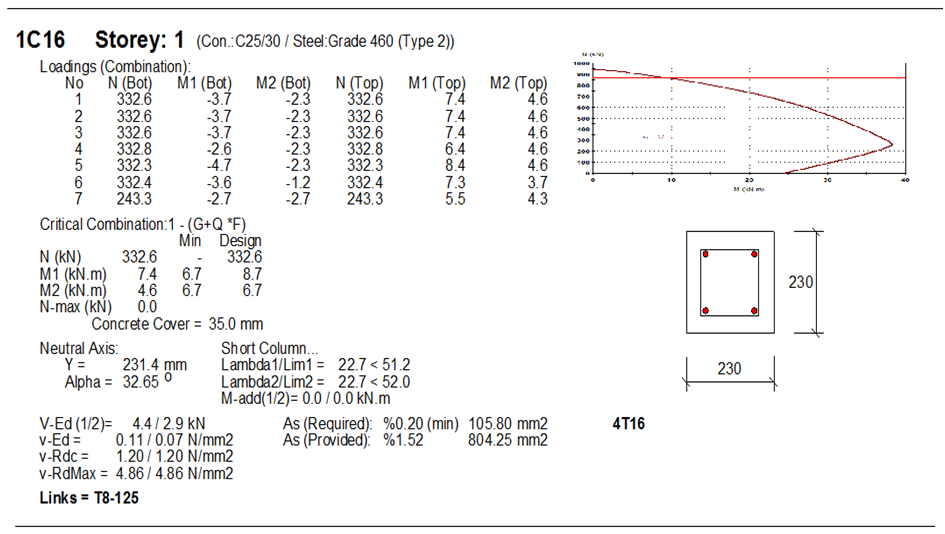
In this post, I am going to present an extremely simplified MATLAB code for carrying out flexural design of reinforced concrete beams (rectangular or flanged) according to Eurocode 2. Before you can use this code, you must carry out your analysis and obtain your design forces and moments. You can just copy the code and paste on your MATLAB script. There are no external functions to be called for the program.

% ANALYSIS AND DESIGN OF RECTANGULAR AND FLANGED BEAMS PER EUROCODE 2
% THIS PROGRAM WILL CALCULATE THE AREA OF REINFORCEMENT REQUIRED, AND ALSO DO THE DEFLECTION VERIFICATION USING THE DEEMED TO SATISFY RULES OF EC2

clc
disp(‘THIS PROFORMA WAS WRITTEN BY O.U.R UBANI’)
disp(‘DOWNLOADED FROM WWW.STRUCTVILLE.COM’)
disp(‘ANALYSIS AND DESIGN OF BEAMS PER EUROCODE 2’)

% INPUT MATERIAL PROPERTIES
Fck = input(‘Enter the grade of concrete (N/mm^2)Fck = ‘);
Fyk = input(‘Enter the yield strength of steel (N/mm^2)Fyk = ‘);

% INPUT DESIGN MOMENT
MEd = input(‘Enter the ultimate design moment (KNm) MEd = ‘);

% INPUT SECTION AND DESIGN PROPERTIES
h = input(‘Enter the depth of beam (mm)h = ‘);
b = input(‘Enter the effective flange width of the beam (mm)b = ‘);
bw = input(‘Enter the beam width (mm)bw = ‘);
Cc = input(‘Enter concrete cover (mm) = ‘);
dr = input(‘Enter the diameter of reinforcement (mm) = ‘);
dl = input(‘Enter the diameter of links = ‘);

% CALCULATION OF EFFECTIVE DEPTH
disp(‘Effective depth d (mm)’)
d = h-Cc-(dr/2)-dl % Effective depth
disp(‘Depth of reinforcement from the face of concrete’)
do = Cc+dl+(dr/2)

% ANALYSIS FOR INTERNAL STRESSES
ko = 0.167;
k = (MEd*10^6)/(Fck*b*d^2)
if k>ko
disp(‘Since k > ko, Compression reinforcement is required’)
Mcd = (Fck*b*d^2*(k-ko))*10^(-6)
As2 = (Mcd*10^6)/(0.87*Fyk*(d-do))
z = 0.5*d*(1+sqrt(1-3.53*ko))
As1 = ((ko*Fck*b*d^2)/(0.87*Fyk*z))+ As2
else
disp(‘Since k < ko, No Compression reinforcement is required’)
disp(‘Lever arm (la)’)
la = 0.5+sqrt(0.25-0.882*k)
if la>0.95
disp(‘Since la > 0.95,’)
la = 0.95
else
la = 0.5+sqrt(0.25-0.882*k)
end
As1 =(MEd*10^6)/(0.87*Fyk*la*d)
end

% MINIMUM AREA OF STEEL REQUIRED
fctm = 0.3*(Fck^(2/3)) %MEAN TENSILE STRENGTH OF CONCRETE (TABLE 3.1 EC2)
ASmin = 0.26*(fctm/Fyk)*bw*d
if ASmin < 0.0013*bw*d
ASmin = 0.0013*bw*d
end
if As1<ASmin
As1 = ASmin
else
disp(‘Since As1 > Asmin, provide As1 which is the area of steel required’)
end

Asprov1 = input(‘Enter area of tension steel provided (mm^2) = ‘);
Asprov2 = input(‘Enter area of compression steel provided if any (mm^2) = ‘);

% CHECK FOR DEFLECTION

disp(‘DO YOU WANT TO CHECK FOR DEFLECTION?’)

G = input(‘ENTER (1) FOR YES OR (0) FOR NO = ‘);

if G == 1;

disp(‘CHECK FOR DEFLECTION’)

disp(‘BASIC SPAN/EFFECTIVE DEPTH RATIO (K)’)

disp(‘CANTILEVER = 0.4’)

disp(‘SIMPLY SUPPORTED = 1.0’)

disp(‘SIMPLY SUPPORTED AND FIXED AT ONE END = 1.3’)

disp(‘FIXED AT BOTH ENDS = 1.5’)

K = input(‘Enter the selected value of k = ‘);

L = input(‘Enter the deflection critical length of the member (mm) = ‘);

disp(‘Fs is the stress in tensile reinforcement under service loading’)

Fs = (310*Fyk*As1)/(500*Asprov1)

disp(‘Bs = 310/Fs’)

Bs = 310/Fs

disp(‘P is the reinforcement ratio in the section (Asprov1)/(b*d)’)

P = (Asprov1)/(b*d)

disp(‘Po = sqrt(Fck)/1000’)

Po = sqrt(Fck)/1000

P1 = (Asprov2)/(b*d)

if

P <= Po

I_deflection = K*(11+(1.5*sqrt(Fck)*(Po/P)) + 3.2*sqrt(Fck)*((Po/P)-1)^1.5)

else

I_deflection = K*(11+(1.5*sqrt(Fck)*(Po/(P-P1))) + 3.2*sqrt(Fck)*((Po/P)-1)^1.5)

end

CV = input(‘Is the beam is flanged? (1) for YES and (0) for NO = ‘)

if CV == 1

disp(‘S is the ratio of beff/bw’)

S = b/bw

bn = (11-(b/bw))/10

if S >= 3.0;

K_deflection = Bs*0.8* I_deflection

else

K_deflection = Bs*bn* I_deflection

end

if L>7000

Limiting_deflection = (7000/L)*K_deflection

else

Limiting_deflection = K_deflection

end

else

Limiting_deflection = Bs*I_deflection

end

Actual_deflection = L/d

if

Limiting_deflection > Actual_deflection

disp(‘Deflection is satisfactory’)

else

disp(‘DEFLECTION IS NOT SATISFACTORY !!!!! Increase depth of beam, or increase area of steel, or both. Then rerun proforma’)

end

2.0 MATLAB CODE FOR SHEAR DESIGN ACCORDING TO EC2

% SHEAR DESIGN IN EUROCODE 2
clc
disp(‘SHEAR DESIGN ACCORDING TO EC2′)
disp(‘THIS PROFORMA WAS WRITTEN BY O.U.R. UBANI’)

% MATERIALS PROPERTIES
Fck = input(‘Enter the grade of concrete (N/mm^2) = ‘);
Fyk = input(‘Enter the yield strength of steel (N/mm^2) = ‘);

VEd = input(‘Enter the value of shear force at ULS (KN) = ‘);

% SECTION PROPERTIES
h = input(‘Enter the depth of beam (mm) = ‘);
bw = input(‘Enter the beam width (mm) = ‘);
Cc = input(‘Enter concrete cover (mm) = ‘);
dr = input(‘Enter the diameter of reinforcement (mm) = ‘);
dl = input(‘Enter the diameter of links = ‘)
d = h-Cc-(dr/2)-dl % Effective depth
do = Cc+dl+(dr/2)

% CALCULATION OF THE SHEAR CAPACITY OF THE SECTION WITH NO SHEAR REINFORCEMENT

Asprov1= input(‘Enter the area of steel provided in the shear zone (mm^2) = ‘) % The reinforcement must exceed the design anchorage length by at least the effective depth
Crd = 0.12
k1= 1+sqrt(200/d)
if k1>2
k1=2
end
disp(‘Reinforcement ratio’)
P1 = (Asprov1/(bw*d))
if P1>0.02
P1 = 0.02
end

% THIS SECTION IS TO BE CONSIDERED IF THERE IS AXIAL FORCE IN THE SECTION
disp(‘Axial force in the section’)
N = input(‘Enter the value of AXIAL FORCE IF ANY(+VE FOR COMP, AND -VE FOR TENSION)(kN) = ‘)
disp(‘Axial stress in the section (Ds)’)
Ds = (N*1000)/(bw*h)
if Ds > (0.2*0.85*Fck)/1.5
Ds = (0.2*0.85*Fck)/1.5
end
k2 = 0.15;
disp(‘Minimum shear stress in the section (N/mm^2)’)
Vmin = 0.035*k1^(1.5)*sqrt(Fck)
disp(‘Concrete resistance shear stress (VRd) (N/mm^2)’)
VRdQ = ((Crd*k1)*(100*P1*Fck)^(1/3)*(bw*d))/1000 % SHEAR FORCE CONTRIBUTION
VRdN = ((k2*Ds)*(bw*d))/1000 % AXIAL FORCE CONTRIBUTION
VRd = VRdQ + VRdN % TOTAL SHEAR RESISTANCE
if VRd < ((Vmin+(k2*Ds))*(b*d))/1000
VRd = ((Vmin+(k2*Ds))*(b*d))/1000
end
if VRd>VEd
disp(‘Since VRd > VEd’)
disp(‘NO SHEAR REINFORCEMENT REQUIRED, PROVIDE NOMINAL LINKS’)
else
if VRd<VEd
disp(‘Since VRd < VEd’)
disp(‘SHEAR REINFORCEMENT REQUIRED, CALCULATE COMPRESSION STRUT CAPACITY’)
disp(‘Assume strut angle (thetha) = 21.8 deg, cot(thetha)= 2.5’)
thetha = 21.8
V1 = 0.6*(1-(Fck/250))
disp(‘Design compressive strength of concrete (fcd) (N/mm^2)’)
fcd = 0.567*Fck
z = 0.9*d
disp(‘Maximum capacity of compression strut (KN)’)
VRDmax = ((b*z*V1*fcd)/(2.9))/1000
if VRDmax > VEd
disp(‘Since VRDmax > VEd’)
disp(‘OK! Calculate diameter and spacing of links’)
ASMINlinks_to_spacing = ((0.08*sqrt(Fck))/Fyk)*b
ASlinks_to_spacing = (VEd*1000)/(z*0.87*Fyk*2.5)
else
disp(‘Since VRDmax > VEd, it means we need a higher strut angle (beta)’)
disp(‘By calculating the strut angle’)
disp(‘Shear stress at the section (N/mm^2)’)
v = (VEd*1000)/(b*d)
beta = (0.5)*asind((v)/(0.153*Fck*(1-(Fck/250))))
if beta>45
disp(‘Since beta < 45 deg, SECTION INADEQUATE FOR SHEAR, INCREASE DEPTH !!!!!’)
else
disp(‘The ratio of Area of steel/spacing of links’)
ASlinks_to_spacing = (VEd*1000)/(z*0.87*Fyk*cotd(beta))
end
end
end
Area_of_legs = input(‘Enter the area of number of legs selected = ‘)
Spacing = input(‘Enter the spacing = ‘)
disp(‘CHECK’)
T = Area_of_legs/Spacing
if T > ASlinks_to_spacing
disp(‘Shear reinforcement is ok’)
else
disp(‘Increase area of steel, or reduce spacing’)
end
end

Like us on Facebook at www.facebook.com/structville

ALSO IN THIS BLOG
Analysis and Design of Continuous R.C. Raker Beam for Stadium using EC2
Two Approaches to the Calculation of Deflection in EC2; Choose a Faster Approach for Yourself

Two Approaches to the Calculation of Deflection in Eurocode 2

By

Ubani Obinna Uzodimma

-

October 20, 2020

The verification of deflection is an important serviceability check in reinforced concrete design. Most designs codes adopt the ‘deemed to satisfy’ rules which limit the deflection to an acceptable depth using Basic Span/Effective depth ratio. This is generally more frequently employed than carrying out the rigorous exact calculation of deflection which is however not
very reliable.

Eurocode 2 has its own set of deemed to satisfy rules, and there are two approaches to calculation of deflection which yields the same result. It is not like that they are two different formulars, but they are just one formular expressed in two different ways. This post shows the two approaches, so that you can select the one you deem fast enough for carrying out your manual calculations.

According to Clause 7.4.2 of EN 1992-1-1, we can verify deflections in the absence of exact calculations using deemed to satisfy basic span/effective depth (limiting deflection to depth/250);

Lateral Deflection of Multi-Storey Buildings Under the Action of Wind Load

(a) BY USING THE FIRST APPROACH
Actual L/d must be ≤ Limiting L/d × β_s

The limiting basic span/ effective depth ratio is given by;
L/d = K [11 + 1.5√(f_ck) ρ₀/ρ + 3.2√(f_ck ) [(ρ₀ / ρ) – 1]^(3⁄2) ] if ρ ≤ ρ₀ ———– (1)

L/d = K [11 + 1.5√(f_ck) ρ₀/(ρ – ρ’) + 1/12 √(f_ck) (ρ₀/ρ)^(1⁄2) ] if ρ > ρ₀ ———— (2)
Where;
L/d is the limiting span/depth ratio
K = Factor to take into account different structural systems
ρ₀ = reference reinforcement ratio = 10^-3√(f_ck)
ρ = Tension reinforcement ratio to resist moment due to design load
ρ’ = Compression reinforcement ratio

The value of K depends on the structural configuration of the member, and relates the basic span/depth ratio of reinforced concrete members. This is given in the Table below;

Table%2Bof%2Bbasic%2Bspan%2Bto%2Beffective%2Bdepth%2Bratio%2BEC2

β_s = (500 As_prov)/(F_yk As_req) ———- (3)

(b) BY USING THE SECOND APPROACH
L/d ≤ Basic ratio × α_s × β_s
Where the basic ratio = 20K

Modification factor α_s which depends on the concrete strength f_ck and reinforcement percentages, is given by:

For 100A_s/bd < 0.1f_ck^0.5;
α_s = 0.55 + 0.0075f_ck/(100A_s/bd) + 0.005f_ck^0.5[ f_ck^0.5/ (100A_s/bd) – 10]^1.5 —————- (4)

For 100A_s/bd ≥ 0.1f_ck^0.5;
α_s = 0.55 + 0.0075f_ck/[100(A_s – A_s’)/bd) + 0.013f_ck^0.25 (100A_s’/bd)]^0.5 (for doubly-reinforced sections) —————- (6)

α_s = 0.55 + 0.0075f_ck/(100A_s/bd) (for singly-reinforced sections) —————- (7)

Modification factor β_s = 310/σ_s —————- (8)
Where:
σ_s is the stress in the tension reinforcement under the characteristic loading. It will normally be conservative to assume;
β_s = (500/f_yk)(A_s,prov/A_s,req) for values of (A_s,prov/A_s,req)≤ 1.5 —————- (9)

Important hints on the calculation of deflection using both approaches;

(1) For flanged sections with b/b_w ≥ 3, the basic ratios for rectangular sections should be multiplied by 0.8. For values of b/b_w < 3, the basic ratios for rectangular sections should be multiplied by (11 – b/b_w)/10

(2) The ratio should be based on the shorter span for two-way spanning slabs, and the longer span for flat slabs.

(3) For beams and slabs, other than flat slabs, with spans exceeding 7 m, which support partitions liable to be damaged by excessive deflections, the basic ratio should be multiplied by 7/span. For flat slabs, where one or both spans exceeds 8.5 m, which support partitions liable to be damaged by excessive deflections, the basic ratio should be multiplied by 8.5/span.

SOLVED EXAMPLE

For the example above we check the deflection for span D-E.
f_ck = 35 N/mm²; f_yk = 460 N/mm²; Effective depth = 840mm; Effective width of flange (B_eff) = 1650mm; A_s,req = 1850 mm²; A_s,prov = 2101 mm²
BY APPROACH 1

ρ = A_s,prov /B_effd = 2101 / (1650 × 840) = 0.0015158;
ρ₀ = reference reinforcement ratio = 10^-3√(f_ck) = 10^-3√(35) = 0.005916
Since if ρ ≤ ρ₀;

L/d = K [11 + 1.5√(f_ck) ρ₀/ρ + 3.2√(f_ck) (ρ₀ / ρ – 1)^(3⁄2)
k = 1.3 (One end continuous)

L/d = 1.3 [11 + 1.5√(35) × (0.005916/0.001516) + 3.2√(35) × [(0.005916 / 0.001516) – 1]^(3⁄2)
L/d = 1.3[11 + 34.630 + 93.608] = 181.00

β_s = (500 As_prov)/(F_yk As_req) = (500 × 2101) / (460 × 1850 ) = 1.234

Check b/b_w = 1650/300 = 5.5
Since b/b_w ≥ 3, multiply L/d by 0.8
Since span is greater than 7m, also multiply by 7/span

Therefore limiting L/d = 1.234 × 0.8 × (7/8) × 181.04 = 156.382
Actual L/d = 8000/840 = 9.523

Since Actual L/d < Limiting L/d, deflection is satisfactory.

BY APPROACH 2

100A_s/bd = (100 × 2101) / (1650 × 840) = 0.1516
Check 0.1f_ck^0.5 = 0.1 × (35)^0.5 = 0.5916

Since For 100A_s/bd < 0.1f_ck^0.5

α_s = 0.55 + 0.0075f_ck/(100A_s/bd) + 0.005f_ck^0.5[ f_ck^0.5/ (100A_s/bd) – 10]^1.5
α_s = 0.55 + [(0.0075 × 35) /(0.1516)] + [0.005 × (35)^0.5 × [(35^0.5/0.1516) – 10]^1.5 = 0.55 + 1.7315 + 4.625 = 6.9065

Basic ratio = 20k = 20 × 1.3 = 26

β_s = (500/f_yk)(A_s,prov/A_s,req) = (500/460) × (2101/1850) = 1.234

Check b/b_w = 1650/300 = 5.5
Since b/b_w ≥ 3, multiply L/d by 0.8
Since span is greater than 7m, also multiply by 7/span

Therefore limiting L/d = 1.234 × 0.8 × (7/8) × 26 × 6.9065 = 155.111
Actual L/d = 8000/840 = 9.523

You can verify that the two methods can be used, with the second method being more approximate.

Like us on Facebook at www.facebook.com/structville

Shear Deformation of Beams Using Virtual Work Method

By

Ubani Obinna Uzodimma

-

May 2, 2022

The predominant cause of deformation in beams subjected to externally applied load is bending, and that is one of the most popular analytical methods for beams with small deflection. However, additional deformation is induced in beams due to shear forces in the form of mutual sliding of adjacent sections across each other. As a result of the non-uniform distribution of shear stresses, the sections previously plane now become curved due to shearing alone.

Beams that are analysed by considering elastic deformation due to bending are known as Euler-Bernoulli beams, while beams that are analysed considering bending and shear deformations are known as Timoshenko beams. Timoshenko beam theory is useful in the analysis of thick beams.

Difference between Euler beam and Timoshenko beam

In this article, we are going to present some solved examples on the shear deformation of one-span beams due to externally applied load. Using the simple virtual work method and employing Verecshagin’s combination rule, we are going to calculate the deflection at the critical points of some beams due to bending and due to shear forces. You will discover why shear deflection is neglected in some cases, but in sections that are significantly deeper, shear forces can be quite influential.

The displacement equation due to shear forces is given below;

Shear%2BDeformation%2BEquation%2BUsing%2BVirtual%2BWork%2BMethod

Where;
k = factor that accounts for non-uniform distribution of shearing stresses. For rectangular sections, k = 3/2, and for circular sections, k = 3/4
G = Shear modulus of the section
A = Area of the cross-section
Q = Shear force due to externally applied load
Q ̅ = Shear force due to a unit virtual load at the point where the deflection is sought

Similarly, the displacement equation due to bending moment is given below;

Beam%2BDeflection%2BEquation%2BUsing%2BVirtual%2BWork%2BMethod

Where;
E = Elastic modulus of the section
I = Moment of inertia of the cross-section
M = Bending moment due to externally applied load
M ̅ = Bending moment due to a unit virtual load at the point where the deflection is sought

Solved Examples
For all examples shown below, the section shown below will be used for all calculations.

Geometrical Properties
Area (A) = bh = 0.2m × 0.4m = 0.08 m²
Moment of inertia (I) = bh³/12 = (0.2 × 0.4³)/12 = 0.0010667 m⁴
E = 21.7 KN/mm² = 21.7 × 10⁶ KN/m²
G = E / 2(1 + ν) = (21.7 × 10⁶)/2(1 + 0.2) = 9.0416 × 10⁶
Flexural rigidity EI = (21.7 × 10⁶) × 0.0010667 = 23147.39 KN.m²
Shear stiffness GA = (9.0416 × 10⁶) × 0.08 = 723333.333 KN

Example 1: Shear deflection of a simply supported beam carrying a uniformly distributed load

The internal forces diagram due to externally applied load is shown below;

Beam%2BNumber%2B1%2BInternal%2BStresses%2Bdiagram%2B%2528UDL%2529

Removing the external load and placing a unit load at the mid-span, we can plot the internal stresses diagram as shown below;

Beam%2BNumber%2B1%2Band%2B2%2BVirtual%2BLoad

We can now obtain the deflection at the mid-span by diagram combination;

(a) Deflection due to bending;

Influence%2Bcoefficient%2BBending%2B%2528Beam%2BNumber%2B1%2529

EIδ_b1 = 2 [5/12 × 62.5 × 1.25 × 2.5] = 162.760
δ_b1 = 162.760/23147.39 = 0.0070314 m = 7.0314mm

(b) Deflection due to shear;

Influence%2Bcoefficient%2BShear%2BBeam%2BNumber%2B1

GAδ_s1 = 2 [3/2 × 1/2 × 50 × 0.5 × 2.5] = 93.75
δ_s1 = 93.75/723333.333 = 0.0001296 m = 0.1296 mm

Example 2: Shear deformation of a simply supported beam carrying a concentrated load at the mid-span.

The internal forces diagram due to externally applied load is shown below;

Beam%2BNumber%2B2%2BInternal%2BStresses%2BDiagram%2B%2528Point%2BLoad%2529

Placing a unit load at the mid-span and plotting the internal stresses diagram;

We can now obtain the deflection at the mid-span by diagram combination;

(a) Deflection due to bending;

Influence%2Bcoefficient%2BBending%2B%2528Beam%2BNumber%2B2%2529

EIδ_b2 = 2 [1/3 × 125 × 1.25 × 2.5] = 260.417
δ_b2 = 260.417/23147.39 = 0.01125 m = 11.25 mm

(b) Deflection due to shear;

Influence%2Bcoefficient%2BShear%2BBeam%2BNumber%2B2

GAδ_s2 = 2 [3/2 × 50 × 0.5 × 2.5] = 187.5
δ_s2 = 187.5/723333.333 = 0.0002592 m = 0.2592 mm

Example 3: Shear deformation of Cantilever beam carrying a uniformly distributed load

bending and shear force diagram of a cantilever

Placing a unit load at the free end and plotting the internal stresses diagram;

We can now obtain the deflection at the mid-span by diagram combination;

(a) Deflection due to bending;

Influence%2Bcoefficient%2BBending%2B%2528Beam%2BNumber%2B3%2529

EIδ_b3 = [1/4 × 250 × 5 × 5] = 1562.5
δ_b3 = 1562.5/23147.39 = 0.0675 m = 67.502 mm

(b) Deflection due to shear;

GAδ_s3= [3/2 × 1/2 × 100 × 5 × 1.0] = 375
δ_s3 = 375/723333.333 = 0.00051843 m = 0.5184 mm

As you can see in all the examples we considered, there was no case where the additional deflection due to shear was up to 1 mm, and for practical purposes, they are very negligible for normal one span beams. Watch out for future posts where we will present cases where shear deflection becomes significant.

Thank you for visiting www.structville.com. We hope you visit us again, and share this post with your friends.

Elastic Settlement of Shallow Foundations

By

Ubani Obinna Uzodimma

-

October 13, 2022

Shallow foundations on natural soils will undergo settlement when loaded. Foundation settlement is mainly made up of elastic (or immediate) settlement, S_e, consolidation settlement, S_c. Immediate settlement takes place as the load is applied, or within a period of about 7 days. It is used for all fine-grained soils including silts and clays with a degree of saturation less than or approximately less than 90%, and for all coarse-grained soils with a large coefficient of permeability, say above 10^-3 m/s. This article presents a solved example of the elastic settlement of shallow foundations.

It is important to point out that, theoretically at least, a foundation could be considered fully flexible or fully rigid. A uniformly loaded, perfectly flexible foundation resting on an elastic material such as saturated clay will have a sagging profile, as shown in the figure above, because of elastic settlement. However, if the foundation is rigid and is resting on an elastic material such as clay, it will undergo uniform settlement and the contact pressure will be redistributed. The settlement at the centre of a rigid foundation can be estimated as, S_e(rigid) ≈ 0.93S_e(flexible).

To assess the immediate settlement of a shallow foundation, it is imperative to obtain reliable values of elastic parameters of the soil. Values from the laboratory can contain errors of about 50%, and in-situ tests are often more preferred, with close attention being paid to the anisotropic behaviour of soils.

A range of values for the elastic properties of soils can be seen in Table 1;

Type of Soil	Modulus of Elasticity E_s(MN/m²)	Poisson’s Ratio
Loose sand	10 – 25	0.20 – 0.40
Medium dense sand	15 – 30	0.25 – 0.40
Dense sand	35 – 55	0.30 – 0.45
Silty sand	10 – 20	0.20 – 0.40
Sand and gravel	70 – 170	0.15 – 0.35
Soft clay	4 – 20
Medium clay	20 – 40	0.20 – 0.50
Stiff clay	40 – 100

Table 1: Elastic properties of soils

It is also necessary to obtain a reliable stress profile from the applied load. We normally have the problem of computing both correct numerical values and the effective depth H of the influence zone. Theory of elasticity equations are used for the stress computation, with the influence depth (H) below the loaded area taken as H = 0, to H = ∞.

However, note that the stratum depth actually causing settlement is not at H/B = ∞, but is at any of the following;

(a) Depth (z) = 5B; where B is the least total lateral dimension of the footing
(b) Depth to where a hard stratum is encountered. Take hard as that stratum where the modulus of elasticity is ten times the modulus of elasticity of the upper layer.

The equation for computing the elastic settlement of a shallow footing is given below;

Where;
q_o = net applied pressure on the foundation
μ_s = Poisson’s ratio of soil
E_S = Average modulus of elasticity of the soil under the foundation from z = 0 to about z = 4B or 5B

Due to the non-homogeneous nature of soil deposits, the magnitude of E_s may vary with depth. For that reason, Bowles (1987) recommended using a weighted average value of E_s as given in equation (2) below;

Weighted%2BAverage%2Bof%2BModulus%2Bof%2BElasticity

Where;
E_S(i) = Soil modulus of elasticity within a depth ∆z
z ̅ = H or 5B, whichever is smaller
B’ = B/2 for the centre of the foundation, B for the corner of the foundation
I_S = Shape factor according to Steinbrenner (1934)

Steinbrenner%2527s%2BInfluence%2Bfactor%2Bequation

Where;

Steinbrenner%2527s%2BInfluence%2Bfactor%2Bequation%2Bparameters

I_f= Depth factor which depends on (D_f/B, μ_s, L/B)

Charts for computing I_f are available in standard geotechnical engineering textbooks.
α = factor that depends on the location on the foundation where settlement is being calculated

For the calculation of settlement at the centre of the foundation;
α = 4; m’= L/B; n’ = H/0.5B
For the calculation of settlement at the corner of the foundation;
α = 1; m’= L/B; n’ = H/B

Worked Example

For the example given below, compute the settlement at the centre of the footing, assuming that a net pressure of 145 kN/m² is exerted by the foundation.

Given that B = 1.8m, L = 2.7m; z ̅ = (5 × 1.8) = 9.0 m = H (9.0 m)

E_s = [12000(5) + 7500(3) + 10200(1.2)] / 9 = 10526.667 KN/m²
At the centre of the foundation;
α = 4; m’= L/B =2.7/1.8 =1.5 ; n’ = H/0.5B=9/(0.5(1.8)) = 10

A₀ = 1.5 In ((1+ (1.5² + 1)^0.5) × (1.5² + 10²)) / 1.5 (1 + (1.5²+ 10² + 1)^0.5)
= 1.5 In(2.803 × 10.112) / (1.5 × 11.161) = 0.7896

A₁ = In ((1.5 + (1.5² + 1)) × (1 + 10²)) / (1.5 + (1.5² + 10² + 1)^0.5)
= In[(3.3027 × 10.049) / (1.5 + 10.161)] = 1.0459

A₂ = 1.5 / [10 (1.5² + 10² + 1)^0.5] = 1.5 / (10 × 10.161) = 0.0147

F₁ = 1/π (A₀ + A₁ ) = 1/π (0.7896 + 1.0459) = 0.5842
F₂ = (n’/2π) tan^-1⁡A₂ = 10/2π tan^-1⁡(0.0147) = 0.0233 (calculated in radians)

Therefore, the shape factor according to Steinbrenner;

I_S = F₁ + [(1 – 2μ_s)/(1 – μ_s)] × F₂ = 0.5842 + [(1 – (2 × 0.3) / (1 – 0.3)] × 0.0233 = 0.5975
From chart, let us obtain the foundation embedment factor (I_f);
D_f/B = 0.9/1.8 = 0.5
L/B = 2.7/1.8 = 1.5

From the chart, say I_f = 0.79
Inputting all the parameters into the elastic settlement equation given in (1)

S_e = q_o α × B’ × ((1- μ_s²)/E_s) × I_s × I_f
S_e = 145 × 4 × 0.9 × ((1 – 0.3²)/10526.667) × 0.5975 × 0.79 = 0.0213m = 21.3 mm

This gives the elastic settlement at the centre of the footing. A lot of modifications and other proposals have been made by scholars over years due to improved research, and we will keep posting them as time goes on.

Keep visiting www.structville.com and tell your folks about it.

Analysis of Three-Hinged Arch Structures

By

Ubani Obinna Uzodimma

-

July 7, 2024

Arches are important structural elements in engineering that provide economical solutions in buildings and bridges. Three-hinged arch structures are pinned at the supports (springings) and somewhere along the barrel, which is usually at the crown. The structural analysis and design of three-hinged arches involve the determination of the internal stresses (bending moment, shear force, axial force, and torsion in the structure due to externally applied load, and providing adequate sections to resist the applied load.

In horizontal beams supporting uniformly distributed load, the bending moment increases with the square of the span and hence they become uneconomical for long-span structures. In such situations, arches could be advantageously employed, since they would develop horizontal reactions, which in turn reduce the bending moment.

A three-hinged arch, which is usually made from steel or timber, is statically determinate. Unlike statically indeterminate arches, they are not affected by differential settlement or temperature changes. Three-hinged arch structures have three natural hinges as the name implies. The two supports are hinged, and another internal hinge is usually located at the crown.

A three-hinged arch has four unknown reactions, i.e., two vertical reactions and two horizontal reactions at the supports. For their determination, three equilibrium equations can be formulated considering the whole of the structure.

Since it is well known that the bending moment at any internal hinge is zero, the internal hinge in the barrel of the arch provides an additional equation for the equilibrium of any part of the system. This means that the sum of the moments of all external forces, which are located on the right (or on the left) part of the structure with respect to the internal hinge is zero. Therefore, a three-hinged arch is a geometrically unchangeable and statically determinate structure. The figure below shows a three-hinged Bolt-laminated Ekki Timber bridge at Finowfurt, Germany.

The peculiar feature of arched structures is that horizontal reactions are induced even when the structure is subjected to vertical load only. These horizontal reactions under vertical loading A_x = B_x = H are called the thrust of the structure. At any cross-section of the arch, bending moments, shear, and axial forces are developed. However, the bending moments and shear forces are smaller than corresponding internal forces in a simply supported beam covering the same span and subjected to the same load.

This fundamental property of the arch is thanks to the thrust developed. Thrusts in both supports are pointed towards each other and consequently reduce the bending moments that would arise in beams of the same span and load configuration. The two parts of an arch may be connected by a tie. In this case in order for the structure to remain statically determinate, one of the supports of the arch should be supported on a roller.

Solved Example on Analysis of a Three-hinged Arch

For the parabolic arch that is loaded as shown below, compute the support reactions and plot the internal stresses diagram for the identified sections. The arch is hinged at points A, B, and C.

SOLUTION
Geometrical properties of the arch
The ordinate (y) at any point along a parabolic arch is given by;

y = [4y_c (Lx – x²)] / L²
Where;
y_c = Height of the crown of the arch from the base
L = Length of arch
x = Horizontal ordinate of interest
Hence, y = [4 × 10 (45x – x²)] / 45²

The general equation of the arch now becomes;
y = (8/9)x – (8/405)x² —————– (1)

Differentiating equation (1) with respect to x
dy/dx = y’ = (8/9) – (16/405)x —————— (2)

From trigonometric relations, we can verify that;
Sin θ = y’/[1 + (y’)²]^0.5 —————- (3)
Cos θ = 1/[1+ (y’)²]^0.5 —————- (4)

From the above relations, we can carry out the calculations for obtaining the geometrical properties of the arch structure.

Let us consider point A (support A of the structure);

We can verify that at point A, x = 0, and y = 0;
From equation (2) above, y’ = 8/9;
Thus,
Sin θ = (8/9)/[1 + (8/9)²]^0.5 = 0.664
Cos θ = 1/[1 + (8/9)²]^0.5 = 0.747

Similarly, let us consider point 3 of the structure;

At point 3, x = 27.5m
From equation (1), we can obtain the value of y as; y = [(8/9) × 27.5] – [(8/405) × 27.5²] = 9.5061m;
The tangent at that point can be obtained from from equation (2); dy/dx = y’ = (8/9) – [(16/405) × 27.5] = – 0.1975
Thus,
Sin θ = (-0.1975)/[1 + (-0.1975)²^0.5 = -0.1937
Cos θ = 1/[1 + (-0.1975)²]^0.5 = 0.9813

For the entire section, it is more convenient to set out the geometrical properties in a tabular form. See the picture below;

Support Reactions

Let ∑M_B = 0; anticlockwise negative
(Ay × 45) – (12 × 22.5 × 33.75) – (25 × 10) – (15 × 6.913) = 0
Therefore, Ay = 210.36 kN

Let ∑M_A = 0; clockwise negative
(By × 45) – (25 × 35) + (15 × 6.913) – (12 × 22.5 × 11.25) = 0
Therefore, By = 84.64 kN

Let ∑M_C^L = 0; anticlockwise negative
(Ay × 22.5) – (Ax × 10) – (12 × 22.5 × 11.25) = 0
22.5Ay – 10Ax = 3037.5 ——— (a)

Substituting, Ay = 210.36 kN into equation (a)
Hence, Ax = 169.56 kN

Let ∑M_C^R = 0; clockwise negative
(By × 22.5) – (Bx × 10) – (25 × 12.5) – (15 × 3.087) = 0
22.5By – 10Bx = 358.8 ——— (b)

Substituting, By = 84.64 kN into equation (b)
Hence, Bx = 154.56 kN

Internal Stresses

Bending Moment
M_A = 0 (hinged support)
M₁ = (210.36 × 7.5) – (169.56 × 5.555) – (12 × 7.5 × 3.75) = 298.294 kN.m
M₂ = (210.36 × 15) – (169.56 × 8.889) – (12 × 15 × 7.5) = 298.181 kN.m
M_C = (210.36 × 22.5) – (169.56 × 10.000) – (12 × 22.5 × 11.25) = 0

Coming from the right hand side;

M_C = (84.64 × 22.5) – (154.56 × 10) – (25 × 12.5) – (15 × 3.087) = 0
M₃ = (84.64 × 17.5) – (154.56 × 9.506) – (25 × 7.5) – (15 × 2.593) = -214.442 kN.m
M₄ = (84.64 × 10) – (154.56 × 6.913) = -222.073 kN.m
M_B = 0 (hinged support)

Shear
Q = ∑V cosθ – ∑H sinθ

Q_A = (210.36 × 0.747) – (169.56 × 0.664) = 44.551 kN
Q₁ = [210.36 – (12 × 7.5)] 0.860 – (169.56 × 0.509) = 17.203 kN
Q₂ = [210.36 – (12 × 15)] 0.959 – (169.56 × 0.284) = -19.040 kN
Q_C^R = [210.36 – (12 × 22.5)] 1.000 – (169.56 × 0.000) = – 59.64 kN
Q₃ = [210.36 – (12 × 22.5)] 0.981 – (169.56 × – 0.193) = – 25.782 kN
Q₄^L = [210.36 – (12 × 22.5)] 0.897 – (169.56 × – 0.443) = – 21.618 kN
Q₄^R = {[210.36 – (12 × 22.5) – 25] × 0.897} – [(169.56 – 15) × (- 0.443)] = 7.452 kN
Q_B = (- 84.64 × 0.747) – [154.56 × (- 0.664)] = 39.402 kN

Axial
N = -∑V sinθ – ∑H cosθ

N_A = (-210.36 × 0.664) – (169.56 × 0.747) = – 266.340 kN
N₁ = – [210.36 – (12 × 7.5)] 0.509 – (169.56 × 0.860) = – 207.085 kN
N₂ = – [210.36 – (12 × 15)] 0.284 – (169.56 × 0.959) = -171.230 kN
N_C = – [210.36 – (12 × 22.5)] 0.000 – (169.56 × 1.000) = -169.560 kN
N₃ = -{[210.36 – (12 × 22.5)] × – 0.193} – (169.56 × 0.981) = -177.849 kN
N₄^L = -{[210.36 – (12 × 22.5)] × – 0.443} – (169.56 × 0.897) = – 178.516 kN
N₄^R = -{[210.36 – (12 × 22.5) – 25] × – 0.443} – [(169.56 – 15) × (0.897)] = – 176.136 kN
N_A = – (-84.64 × – 0.664) – (154.56 × 0.747) = – 171.657 kN

Internal Stresses Diagram (Not to scale)

Like us on www.facebook.com/structville

Thank you for visiting.

Deflection of Statically Indeterminate Frames

By

Ubani Obinna Uzodimma

-

May 23, 2022

The deflection of statically indeterminate frames can occur under the action of externally applied loads, temperature difference, or differential settlement of support. These deformations are often expressed in the form of deflections (translations) and rotations (slope). The knowledge about the deformation of structures is very important in that we normally verify the serviceability limit state of structures through them. By being able to limit the deflections in a building, we can make the appearance pleasant, and protect the supported partitions and finishes from cracking.

The definition of slope and deflection is represented in the picture below, showing a simply supported beam deflecting under the action of a concentrated load P.

One of the methods of computing the deflection of statically indeterminate frames is the force method (virtual work method). In this approach, the frame is analysed using the force method, and the bending moment diagram due to the externally applied load obtained. Furthermore, a unit virtual load is placed on the basic system of the structure at the point where the deflection is sought, and analysed to also obtain the bending moment diagram. Using Verecschagin’s rule, it is possible to combine the bending moment diagram from the externally applied load with the moment diagram due to the virtual load to obtain the deflection at that point.

To learn how to apply force method to the analysis of indeterminate frames, click HERE
To learn about Vereshchagin’s rule, click HERE

In this post, we are going to calculate the vertical deflection at point B of the frame loaded as shown below. A little consideration will show that the frame is indeterminate to the 3rd order. See previous posts on how to verify the determinacy of structures. Take EI = Constant

(1) Step 1
Reduce the structure to a basic system. A basic system is a system that is statically determinate and stable. The adopted basic system is as shown below;

(2) Step 2
Replace the support reactions with unit loads and analyse each load case independently. Furthermore, plot the bending moment due to the individual virtual loads. These diagrams can be plotted without finding support reactions. The different load cases and their corresponding bending moment diagrams are shown below;

CASE 1

CASE 2

CASE 3

(3) Step 3

Place the external load on the basic system, and plot the bending moment diagram.

(4) Step 4
Combine the various bending moment diagrams using the Verecschagin’s rule, and obtain the influence coefficients.

δ₁₁ = Deflection at point 1 due to unit load at point 1

δ₁₁ = 1/3(3 × 3 × 5) + (3 × 3 × 6) + 1/3(5 × 5 × 5) + 1/3(3 × 3 × 3) = 119.667/EI

δ₁₂ = δ₂₁ Deflection at point 1 due to unit load at point 2

δ₁₂ = 1/3(3 × 4 × 5) + 1/2 [4 × (4 +10) × 6] – 1/2(5 × 5 × 10) – 1/2(3 × 3 × 10) = 66/EI

δ₁₃ = δ₃₁ Deflection at point 1 due to unit load at point 3

δ₁₃ = -(3 × 3 × 6) + 1/6 [5 × (22 + 6) × 5] – 1/6 [3 × (6 + 6) × 3] = 44.667/EI

δ₂₂ = Deflection at point 2 due to unit load at point 2

δ₂₂ = 1/3(4 × 4× 5) + 1/6 [4(8 + 10) + 10(20 + 4) ] × 6 – (8 × 8× 10) = 1138.667/EI

δ₂₃ = δ₃₂ Deflection at point 2 due to unit load at point 3

δ₂₃ = – 1/2 [3 × (4 +10) × 6] – 1/2 [10 × (11 + 3) × 8] = -686/EI

δ₃₃ = Deflection at point 3 due to unit load at point 3

δ₃₃ = 1/3(3 × 3× 3) + (3 × 3× 6) + 1/6 [11(22 + 3) + 3(6 + 11) ] × 8 = -497.667/EI

δ₁₀ = Deflection at point 1 due to externally applied load

δ₁₀ = 1/3(160 × 8) × 3 = -1280/EI

δ₂₀ = Deflection at point 2 due to externally applied load

δ₂₀ = 1/3(160 × 8 × 10 ) = -128/EI

δ₃₀ = Deflection at point 3 due to externally applied load

δ₃₀ = 1/12 [160 × (33 + 3) × 8] = – 384/EI

(5) Step 5
Insert the influence coefficients into the appropriate canonical equation and solve for X₁, X₂, and X₃ which are the support reactions at the points where they are required.

119.667X₁ + 66X₂ + 44.667X₃ = 1280
66X₁ + 1138.667X₂ – 686X₃ = – 4266.667
44.667X₁ – 686X₂ + 497.667X₃ = 3840

On solving;
X₁ = 8.196 kN;
X₂ = -0.09887 kN;
X₃ = 6.844 kN

(6) Step 6
Obtain the final bending moment values and plot the diagram

Final Moments

M_i = M₀ + M₁X₁ + M₂X₂ + M₃X₃

M_A = -160 + (8.196 × 5) – (-0.09887 × 10) + (6.844 × 11) = -42.7473 kNm
M_B = (8.196 ×- 3) – (-0.09887 × 10) + (6.844 × 3) = -3.0673 kNm
M_C^B = (8.196 ×- 3) – (-0.09887 × 4) + (6.844 × 3) = -3.660 kNm
M_C^L = (8.196 × 3) + (-0.09887 × 4) =24.19252 kNm
M_C^R = (6.844 × 3) = 20.532 kNm

The final bending moment diagram is shown below.

(7) Step 7
Place a unit vertical load at point B of the basic system and plot the bending moment diagram

(8) Step 8
Combine the resulting bending moment diagram with the final moment diagram form the externally applied load to obtain the deflection at point B. However, you should know that the complex bending moment on our final bending moment diagram can actually be split as shown below;

The subsequent combination to obtain the vertical deflection at point B is as shown below;

Deflection of statically indeterminate frames

Therefore, the vertical deflection at point B;
δ_B = 1/3(42.747 × 8 × 8) – 1/3(40 × 8 × 8) + 1/6(3.067 × 8 × 8) = 91.318/EI metres

Thank you for visiting, and God bless you.

Like us on www.facebook.com/structville

Blast Resistant Structures: 21 Things You Should Know

By

Ubani Obinna Uzodimma

-

February 13, 2020

Explosives continue to be the terrorist’s preferred weapon, since they are destructive, relatively easy to obtain or fabricate, and still comparatively easy to move surreptitiously on the ground and by sea. Terrorists are also well aware that explosives produce fear in the general population far beyond the geographical location of their intended target.

On the 26th of August, 2011, a car bomb attacked the UN Building in Abuja, the capital of Nigeria, after breaking through two security barriers. The attack claimed about 21 lives, and wounded about 60. A wing of the building collapsed, and the ground floor was severely damaged.

There seems to be a sense of anxiety about the vulnerability of our buildings, bridges, tunnels, and utilities in the midst of numerous recognized international social and political instabilities, and given the potential for domestic groups and individuals to seek influence and create disruption by resorting to violent means. As a result, consultants designing buildings may be expected to provide advice and sometimes specific enhancements in response to quantifiable threats, as well as perceived vulnerabilities.

This post explains 21 basic things you should know about the design of blast resistant structures.

(1) An explosion is a violent thermochemical event

Explosion Image by US Department of Defense

It involves supersonic detonation of an explosive material, violently expanding hot gases, and radiation of a shock front that has peak pressures that their magnitude is higher than those that buildings normally experience under any other loadings.

(2) Building an effective security and risk assessment team

A comprehensive risk assessment for blast-protection design involves close collaboration among city planners, architects, engineers, blast consultant subject matter experts, and law enforcement security professionals. In this group effort, collaborating professionals assess and select the security measures needed to detect, deter, prevent, defeat, mitigate, or recover from terrorists’ bomb attacks.

(3) Nature of blast impact

When the shock front radiating from a detonation strikes a building component, it is instantaneously reflected. This impact with a structure imparts momentum to exterior components of the building. The associated kinetic energy of the moving components must be absorbed or dissipated in order for them to survive. Generally, this is achieved by converting the kinetic energy of the moving facade component to strain energy in resisting elements.

(4) Mmmm… Not the whole structure may collapse

CihP92jXAAEVGZY 1463343433781 1316043 ver1.0%25281%2529

Structures as a whole generally are not pushed over by a common explosion. The overall mass of a structure is usually large enough to keep the kinetic energy imparted to the structure as a whole small enough that it can be absorbed by the multiple elements that would need to fail before the building topples.

(5) Stand-off distance (assumed location of explosion) is very important during assessment

Distance is the single most important asset to a structural engineer designing for blast resistance. The farther the explosion is from the structure, the lower are the effects that the structure must resist. Further, there often is merit to the construction of blast walls or line-of-sight barriers to add protection to a facility.

(6) Keep it confidential

When blast-resistant designs are for the security and safety of a facility/building in response to a threat of a malevolent attack, information about the assumed size and location of an explosion should be kept confidential. This information could be useful to an aggressor because it can reveal a strategy to overwhelm the designed defenses.

(7) Facades and fenestration can turn to missiles

The catastrophic fracturing of building materials such as facades, windows, glazing, and leakage of pressure in response to a blast often can be destructive to the interiors of buildings, even when the facades of those buildings are designed to resist the effects of an explosion. These can turn to missiles and occupant injuries are very possible should the design base explosion occur. Except when the most restrictive approaches to blast-resistant design are employed (e.g., with elastic response, so a building can remain functional). Airborne glass fragmentation continues to be identified as one of the most lethal aspects of building component responses to explosive events.

(8) Mass of a building and occupancy load can be beneficial

Blast effects usually are impulsive, meaning that they impart velocity to objects through development of momentum. With momentum being proportional to the product of mass and velocity, and kinetic energy being proportional to the product of mass and velocity squared, the larger the mass, the smaller the velocity and, hence, the smaller the energy that must be dissipated through strain. Therefore, additional mass to a building can be beneficial during an explosion.

(9) Provision for column failure and redistribution of stresses

main qimg 64a2f997363e48efe3a163414f9fbbb5 c

Consultants designing for blast often provide for the possibility that a column will be severely damaged by an explosion, in spite of our best efforts at prevention. When consultants assume that a column has lost its strength, they must develop alternative load paths to prevent a collapse from progressing from the initially damaged column through the structure. One form of alternative resistance involves making beams strong and ductile enough to span over the area of damage, thereby redistributing the load on the damaged column to adjacent columns.

(10) Emergency response considerations

Designers working to enhance blast resistance must consider occupant exit and the needs of emergency responders. Blast resistance invariably includes windows with blast-resistant glass. By definition such glass is difficult to break. Firefighters will need to use special tools and engage unusual tactics to fight a fire in a building that is difficult to enter and vent, and that has features that inhibit extraction of trapped occupants. Designers might need to compensate for blast-resistance features, or enhance fire resistance.

(11) Magnitude of design pressure

Figure 1 Typical blast wave pressure time history

Designers need to understand that the magnitudes of the pressures that an explosion imparts to a structure are highly dependent on the nature of the explosive material, the shape and casing of the device, the size and range of the explosion, the angle of incidence between the advancing shock front and the impacted surface, the presence of nearby surfaces that restrict the expansion of hot gases or that reflect pressure fronts, and the robustness of the impacted surface itself.

(12) Extensive damage of structures during a blast

In many explosions that cause extensive destruction, the damage develops in two phases:
(i) the energy released by the explosion degrades or destroys important structural elements, and
(ii) the damaged structure is unable to resist gravity and collapses beyond the area of initial damage.

(13) Individual elements are often treated as nonlinear SDOF elements

It is common in blast-resistant design to treat individual elements as single degree-of-freedom nonlinear systems. Performance is judged by comparison of response to limiting ductility factors (i.e., the ratio of peak displacement to displacement at yield) or support rotations, with the response calculated as though the structural element were subjected to a pressure function while isolated from other structural influences.

(14) Column integrity is the key

Typically, columns are the component whose integrity is key to sustaining the capability of a building’s structural system to survive a blast load. As such, attention to ensuring their survival should have the highest priority when the blast resistance of a building is to be upgraded.

(15) Beware of fragmentation

Injury and structural damage during an explosion may result not only from the direct pressure and impulse of an air blast, but also from the impact of flying objects called debris and fragmentation. Military weapons are typically explosive charges with some type of metal casing. Upon detonation, this case is ruptured and expelled as fragmentation at high velocity. Similarly, terrorist devices may be embedded with objects such as ball bearings or nails that will be ejected at high velocity. Other fragmentation may occur as objects interact with the blast wave created from a detonation and become airborne.

(16) Blast design is different from seismic design

The conventional approach to blast design is similar to that for seismic design, in two important ways:

(i) both loadings clearly are dynamic and, hence, solutions are energy-based, and

(ii) the way we detail structural elements determines the effective loads for which structures must be designed (meaning, we limit the strength we need to supply by allowing post-elastic behavior to dissipate energy).

However, blast loading, with its extremely fast rise time and usually short duration, is either dynamic or impulsive, depending on the nature of the explosive, its distance from the subject structure, and the level of confinement that the structure creates for the expanding hot gases.

(17) You may have to tolerate more damage

While we tolerate some damage in earthquakes, to dissipate energy, we usually allow more damage for blast events. We expect facades to sustain severe damage. In fact, blast-resistant design often tolerates breaching of the building enclosure (with attendant risk of fatalities) and even sometimes partial collapse of buildings.

(18) Reversal of stresses on floor slabs

Blast-related upward impulses on floor slabs can reverse force distributions in these structural elements. In systems that are not strong and ductile enough for these reversed forces, blast-induced deflection can fracture structural elements that are required to resist gravity loads. Hence, floor systems can fail after the direct effects of the blast pass and the slab falls back downward under the influence of gravity.

(19) Consider the effectiveness of post-event evacuation functions

While the immediate devastating effects of explosive events can be limited by protective design strategies, post-event evacuation functions and the subsequent activities of rescue and recovery are dependent upon the integrity of stairs, vertical transportation systems, power, lighting, voice communication, smoke management, and other systems. These systems can be placed out of service throughout the building or suffer disproportionate damage if they are not specifically designed in response to the project design basis explosive threats.

(20) Engage only licensed and experienced professionals

Blast resistance designers must be licensed design professionals who are knowledgeable in the principles of structural dynamics and experienced with their proper application in predicting the response of elements and systems to the types of loadings that result from an explosion, or they must work under the direct supervision of licensed professionals with appropriate training and experience.

(21) Threat Elimination remains the overall best option

Finally, elimination of the explosive event threat and the reduction of building materials and contents that have the opportunity to participate as fuel sources in the fire development triad of oxygen, fuel load, and an ignition source remains the most attractive, competent, and cost-effective process in developing designs for facilities on any site. However, based on the threat assessment, it may be unreasonable to assume that the facility will not be exposed to explosive event effects.

Disclaimer:
I do not claim ownership to the pictures used in this post. All pictures used here belong to their respective owners, of which it is a little bit impractical to recognise them all.

Information for this article is extracted from: Donald O. Dusenberry (2010): Handbook for Blast-Resistance Design of Buildings. John Wiley and Sons Inc.

Thank you for visiting, and may we remain determined in our struggle to make the world free from hatred, discrimination, violence, terrorism, poverty, and crime. God bless you as you discuss and share.

Your friend,
Ubani Obinna Ranks

Application of Finite Difference Method to the Elastic Analysis of Simply Supported Thin Plates

By

Ubani Obinna Uzodimma

-

December 5, 2020

A plate is a structure whose thickness is comparatively smaller compared to its lateral dimensions. A typical example of a plate is the floor slab commonly found in our buildings. Other examples that you can think of are sheets of steel, the panes of glass windows in your homes, or even sheets of plywood. A typical concrete plate is shown in the picture below. In this post, we are interested in the linear analysis of isotropic and homogeneous plates.

Plates are used as structural members to support and transmit loads and as such, they can be subjected to bending moment, shear force, axial force, and twisting moments. The load-carrying action of a plate is similar, to a certain extent, to that of beams or cables and therefore, plates can be approximated by a gridwork of an infinite number of beams, or by a network of an infinite number of cables, depending on the flexural rigidity of the structure (Ventsel and Krauthammer, 2001).

Plates generally behave like two-dimensional structures. By implication, the loads applied on a plate are carried in two directions, and given the significant twisting rigidity of plates, a plate is stiffer than a beam of comparable span and thickness (Ventsel and Krauthammer, 2001). This two-dimensional structural action of plates results in lighter structures, and therefore offers numerous economic advantages. The bending properties of a plate depend greatly on its thickness than on any of its dimensions (Timoshenko and Woinowsky-Krieger, 1987).

Plates deform when loaded. If the deflections of a plate are small compared to its thickness, then the ‘small deformation theory’ applies, which makes the following assumptions:

1.There are no stresses in the middle plane of the plate. Hence, there are no stresses in the neutral axis during bending.
2.The points that are lying perpendicularly to the middle plane before bending remain perpendicular to the middle plane after bending.
3.The normal stresses in the transverse direction can be neglected.

By following these assumptions, the stresses on the plates can be expressed as a function of the deflection of the plate w, which is a function of the two coordinates (x,y) of the plate (Timoshenko and Woinowsky-Krieger, 1987). The governing differential equation for the deflection of thin plate under pure bending is based on the biharmonic equation shown below;

Before now, the common methods of analysis of thin plates have been the tedious classical solution using either the trigonometric or double series solution (Aginam et al, 2012). These days, numerical methods like Finite Element Method, Boundary Element Method, Finite Strip Method, Gridwork Method, Finite Difference Method, etc have become very popular due to their very easy modelling and programming into computer software.

However, finite element analysis is more prominent. In this article, the application of the finite difference method to the pure bending analysis of a thin plate simply supported on all sides has been presented. The result obtained has been compared with the results from other types of solutions.

Finite Difference Method of Analysis of Thin Plates

The finite difference method is a numerical solution to partial differential equations. When we have a function of two real variables f(x,y) that satisfies a given differential equation, we can evaluate f(x,y) numerically by laying a rectangular grid over the domain, and evaluate f(x,y) at the nodes – the points where the lines of the x-axis and y-axis intersect (For basic introduction you can see, Advanced Engineering Mathematics, Stroud and Booth, 2003).

Consider the 2-D network shown below

Let the vertical spacing of the grid be h, and the horizontal spacing be k.
From our knowledge of numerical approximation of derivatives using Taylor series expansion;

∂w/∂x = (Δx.w)/2h = (w_b – w_a)/2h = 1/2h [w (x + h, y) – w(x – h, y)]
∂w/∂y = (Δy.w)/2k = (w_d – w_g)/2k = 1/2k [w(x, y + k) – w(x, y – k)]

Analogously, for higher-order differentials;
∂²/∂x² = ∂/∂x (∂w/∂x) = (Δx² w)/h² = (w_b – 2w ₀ – w_a)/h² = 1/h² [w(x+h, y) – 2w(x,y) + w(x-h, y)]
∂²/∂y² = ∂/∂y (∂w/∂y) = (Δy² w)/k² = (w_d – 2w₀ – w_g)/k²= 1/h² [w(x, y + k) – 2w(x, y) + w(x, y – k)]

For the pure bending biharmonic equation;
(∂⁴ w)/∂x⁴ + (2∂⁴ w)/(∂x² ∂y² ) + (∂⁴ w)/∂y⁴ = P(x,y)/D, we have;

(20w₀ ) – 8(w_a + w_b + w_d + w_g) + 2(w_c + w_e + w_f ) + w_h ) + 1.0(w_i +w_j + w_k + w_l )= (P₀ α⁴)/D

These expressions are often represented as patterns or computational molecules for the easy computation of the numerical solutions. The biharmonic equation pattern for computing the displacement at the interior nodes are as shown as below.

Support Conditions
For simply supported and fixed supports, we know that the deflection at those points is equal to zero. In order to formulate the boundary conditions, let us consider the interior point 0 in the figure below.

You should know that at that interior point, the biharmonic equation holds true. Let us assume that points a, c, f constitutes the boundary of the plate that is simply supported, and let node i represent a fictitious node created outside the plate boundary. A little consideration will show that for w_a to be zero, we have to eliminate the deflection w_i, obtained by the continuation of the network beyond the boundary of the plate. This is easily done by setting w₀ = -w_i for simply supported plates (See David Johnson, Advanced Structural Mechanics, 2000).

Solved Example
Let us show how the finite difference method can be applied in the analysis of thin plates subjected to uniform lateral pressure of 5 kN/m². The plate is square with dimensions of 6m x 6m and simply supported on all sides. The data of the plate is as shown below;

Application of Finite Difference Method to the Elastic Analysis of Simply Supported Thin Plates 167

The plate has been represented with gridlines that have 6 divisions on all the planar dimensions. Therefore, h = k = 1.0. This shows that the gridline aspect ratio (α) = 1.0. The gridlines have been extended by fictitious nodes, in order to capture the boundary conditions. The nodes have been numbered, and all the points where the deflections are expected to be the same due to the symmetry of the plate and the loading condition have been given the same numbering.

By implication, we have seven distinguished nodes, hence, we are going to solve a 7 x 7 matrix, which can be readily solved using Microsoft Excel or MATLAB. The computational molecule (biharmonic operator/pattern) used is the one shown below. We place the computational molecule node by node and generate the appropriate equation for each node. After the equations are generated, they are arranged as appropriate and solved. The results obtained from this method have been compared with the results from the classical solution and finite element analysis.

Since h = k, the representative computational molecule is given below;

P(x,y)/D = (P₀ α⁴)/D
D = (Eh³) / [12(1- v²)] = (21.7 × 10⁶ × 0.12³) / [12(1 – 0.2²)] = 37497.6/11.52 = 3255 kN/m²
(P₀ h⁴)/D= (5 × 1.0⁴/3255= 0.001536098

Node 1
20w₁ – 8(4w₂) + 2(4w₄) + 1(4w₃) = 0.001536098

Node 2
20w₂ – 8(2w₄ + w₁ + w₃) + 2(2w₂ + 2w₅) + 1(2w₇ + w₂ + 0) = 0.001536098

Node 3
20w₃ – 8(2w₅ + w₂ + 0) + 2(2w₄ + 0) + 1(2w₆ + w₁ + w₃) = 0.001536098

Node 4
20w₄ – 8(2w₄ + w₅ + w₇) + 2(2w₃ + w₁ + w₆) + 1(2w₇ + 0 + 0) = 0.001536098

Node 5
20w₅ – 8(w₃ + w₄ + w₆) + 2(w₇ + w₂) + 1(w₅ + w₂ – w₅ + 0) = 0.001536098

Node 6
20w₆ – 8(w₅ + w₇) + 2(w₄) + 1(2w₃ – w₆ – w₆) = 0.001536098

Node 7
20w₇ – 8(w₃ + w₄ + w₆) + 2(w₂ + w₅) + 1(w₂ + w₇ – w₇ + 0) = 0.001536098

Arranging in matrix form;

On solving;
w₁ = 0.008059 m = 8.059mm (maximum deflection at the midspan of the plate)
w₂ = 0.007062 m
w₃ = 0.004202 m
w₄ = 0.006192 m
w₅ = 0.00369 m
w₆ = 0.002211 m
w₇ = 0.00369 m

On comparing with other methods;

Classical Solution from (Timoshenko and Woinowsky-Krieger, 1987, Table 8, Page 120)
Maximum deflection = 0.00406qa⁴/D = (0.00406 × 5 × 6⁴)/3255 = 0.00808258 m

A little consideration will show that there is a percentage difference of 0.2917% between the answer from the classical method and FDM.

FEA result from Staad Pro (Mesh Size Division = 11 x 11)

Maximum deflection is 0.008228 m
A little consideration will show that there is a percentage difference of 2.0539% between the answer from FEM and FDM.

Conclusion
We can see that the finite difference method can be a handy solution to the analysis of thin plates. The method can be easily programmed on computer software, and the method generally yields lower bound solution.

REFERENCES
(1) Aginam C.H., Chidolue C.A., Ezeagu C.A.(2012): Application OF Direct Variational Method in the Analysis of Isotropic Thin Rectangular Plates. ARPN Journal of Engineering and Applied Sciences VOL. 7, NO. 9, ISSN 1819-6608 pp 1128 – 1138
(2) David Johnson (2000): Advanced Structural Mechanics. Thomas Telford Publishing ISBN: 0 7277 2860 1
(3)Timoshenko S. and Woinowsky-Krieger S. (1987): Theory of plates and shells (2nd Edition). McGraw Hill Book Company
(4)Ventsel E., Krauthammer T. (2001): Thin Plates and Shells Theory, Analysis, and Applications. Marcel Dekker, Inc New York. ISBN: 0-8247-0575-0

To contact the author, send an e-mail to ubani@structville.com or send a Whatsapp message to +2347053638996. Please keep visiting the blog. God bless you.

Like us on www.facebook.com/structville

Example on the Analysis of Statically Determinate Frames (Part 2)

By

Ubani Obinna Uzodimma

-

February 13, 2020

If you missed the PART 1 of this post, click HERE

Problem 1
A statically determinate frame is loaded as shown above. There are internal hinges at B and D, while member EF is hinged at point F. Draw the bending moment, the shear force, and the axial force diagrams.

SOLUTION

Notations
M_i^R – Bending moment at point i, just to the right
M_i^L – Bending moment at point i, just to the left
Q_i^R – Shear force at point i, just to the right
Q_i^L – Shear force at point i, just to the left

(a) Support Reactions

Let ∑M_E = 0 (clockwise positive)
10Ay + M_A – (25 × 5) – [(10 × 3²) / 2) + [(10 × 3²) / 2) + (15 × 5) = 0
10Ay + M_A = 50 ————– (1)

Let ∑M_D^L = 0 (clockwise positive)
7Ay + M_A – 4Ax – (25 × 2) = 0
7Ay + M_A – 4Ax = 50 ————— (2)

Let ∑M_B^Below = 0 (clockwise positive)
3Ay + M_A – 4Ax = 0
3Ay + M_A– 4Ax = 0 ————— (3)

From equation (1);
M_A = 50 – 10Ay —————— (1a)

Substituting the value of M_A in equation (1a) into equations (2) and (3), we obtain respectively;
7Ay – 4Ax + 50 – 10Ay = 50
– 3Ay – 4Ax = 0 ————– (4)

3Ay + 50 – 10Ay – 4Ax = 0
– 7Ay – 4Ax = – 50 —————– (5)

Solving equations (4) and (5) simultaneously;
Ay = 12.5 KN
Ax = – 9.375 KN

Hence;
M_A= 50 – 10(12.5) = – 75 KNm

At this point, it is very possible for us to sum up vertical and horizontal forces in order to obtain the rest of the reactive forces, but let us still obtain them by taking moments (this is very useful since it can serve as a check for correctness of results).

Let ∑M_D^R = 0 (anticlockwise positive)
3Ey – 4Ex – (15 × 8) – (10 × 6 ×3) = 0
3Ey – 4Ex = 300 —————- (6)

Let ∑M_B^R = 0 (anticlockwise positive)
7Ey – 4Ex – (15 × 12) – (10 × 6 ×7) – (25 ×2) = 0
7Ey – 4Ex = 650 —————– (7)

Solving equations (6) and (7) simultaneously;
Ey = 87.5 KN
Ex = – 9.375 KN

Equilibrium check;
∑Fy↓ = 25 + (10 × 6) + 15 = 100 KN
∑Fy↑ = 12.5 + 87.5 = 100 KN

This shows that the requirement for static equilibrium is satisfied,. You can also verify for the horizontal reaction at the supports.

Before we go ahead and obtain the bending moment and shearing forces, let us obtain the axial forces in members DE and DF. Since they are pinned at both ends, they are primarily trusses and will not develop any bending moment or shear force.

γ = tan^(-1)⁡(4/3) = 53.130°
cos γ = 0.6
sin γ = 0.8

∑Fy = 0
87.5 + F_EDsin⁡ γ + F_EFsin⁡γ = 0
0.8F_ED + 0.8F_EF = – 87.5 —————– (8)

∑Fx = 0
9.375 – F_EDcos ⁡γ + F_EFcosγ = 0
-0.6F_ED + 0.6F_EF = – 9.375 ——————- (9)

Solving equations (8) and (9) simultaneously;
F_ED = – 46.875 KN (compression)
F_EF = – 62.5 KN (compression)

These forces are now resolved into their vertical and horizontal components at the points they are attached to the beam as shown below;

(b) Internal Stresses

MEMBERAB (0 ≤ z ≤ 5)
Bending Moment
Mz = (Ay.cos⁡γ.z) – (Ax.sin⁡γ.z) – M_A
Mz = (12.5 × 0.6 × z)- (-9.375 × 0.8 × z) – 75 = 15z – 75

At z = 0;
M_A = -75 KNm

At z = 5m
M_B^Below = 15(5) – 75 = 0

Shear Force
Qz = (Ay.cos⁡γ) – (Ax.sin⁡γ)
Qz = (12.5 × 0.6) – (-9.375 × 0.8) = 15 KN (constant shear force all through the member)

Axial Force
Nz = – (Ay.sin⁡γ) – (Ax.cos⁡γ)
Qz = – (12.5 × 0.8) – (-9.375 × 0.6) = – 4.375 KN (constant axial force all through the member)

MEMBER BD (3 ≤ x ≤ 7)

Bending Moment
The general moment equation for the member is given by;
Mx = Ay.x + (Ax × 4) – M_A – 25(x – 5)
Mx = 12.5x + (9.375 × 4) – 75 – 25(x – 5)
Mx = 12.5x – 37.5 – 25(x – 5)

You can however notice that for section BC, the last term of the general equation will not be involved since we cannot have a negative distance on the beam. Therefore it is not very wise to expand the equation yet.

At x = 3m;
M_B^R = 12.5(3) – 37.5 = 0

At x = 5m;
M_C = 12.5(5) – 37.5 – 25(5 – 5) = 25 KNm

At x = 7m;
M_D = 12.5(7) – 37.5 – 25(7 – 5) = 0

Shear Force
Q_B^R – Q_C^L = 12.5 KN
You can verify that the valid equation for moment at the section (B^R – C^L) is given by;

Mx = 12.5x – 37.5

If we differentiate the equation for moment, we obtain the equation for shear;
(∂Mx)/∂x = Qx = 12.5 KN

You can also verify that the valid equation for moment at the section (C^R – D^L) is given by;
Mx = 12.5x – 37.5 – 25(x – 5) = -12.5x + 87.5
(∂Mx)/∂x = Qx = -12.5 KN
Hence, Q_C^R – Q_D^L = -12.5 KN

Axial Force
You can verify that for section B^R – D^L
N_B – Ax = 0
Hence N_B = 9.375 KN (tension)

MEMBER DF (7 ≤ x ≤ 13)

Bending Moment
Mx = Ay.x + (Ax × 4) – M_A – 25(x – 5) + 37.5(x – 7) – [10(x – 7)²) / 2
Mx = 12.5x + (9.375 × 4) – 75 – 25(x – 5) + 37.5(x – 7) – [10(x – 7)²) / 2
Mx = 12.5x – 37.5 – 25(x – 5) + 37.5(x – 7) – 5(x – 7)²

At x = 7m;
M_B^R = 12.5(7) – 37.5 – 25(7 – 5) = 0

At x = 10m (mid-span);
M_mid = 12.5(10) – 37.5 – 25(10 – 5) + 37.5(10 – 7) – 5(10 – 7)² = 30 KNm

At x = 13m;
M_F^L = 12.5(13) – 37.5 – 25(13 – 5) + 37.5(13 – 7) – 5(13 – 7)² = – 30 KNm

Shear Force
You can verify that the valid equation for moment at section D just to the right (D^R) is;
Mx = 12.5x – 37.5 – 25(x – 5) + 37.5(x – 7) = 25x – 175
(∂Mx)/∂x = Q_D^R = 25 KN

The valid equation for moment at section F just to the left (F^L) is;
Mx = 12.5x – 37.5 – 25(x – 5) + 37.5(x – 7) – 5(x – 7)²
Mx = 12.5x – 37.5 – 25x + 125 + 37.5x – 262.5 – 5(x² – 14x + 49)
Mx = -5x² + 95x – 420
(∂Mx)/∂x = Qx = -10x + 95

Maximum span moment
The maximum moment at the span can be obtained by considering the bending moment equation unique for the section.

Mx = -5x² + 95x – 420
(∂Mx)/∂x = Qx = -10x + 95

Since the maximum moment occurs at the point of zero shear, let us equate the expression for the shear force to zero, and then solve for x;

Such that x = 95/10 = 9.5m
M_max = -5(9.5)² + 95(9.5) – 420 = 31.25 KNm

At x = 13m;
Q_F^L = -10(13) + 95 = -35 KN

Axial Force
For section D^L – F^R
N – Ax – 28.125 = 0
Hence N = 9.375 + 28.125 = 37.5 KN (tension)

MEMNER FG (coming from the right for simplicity) (0 ≤ x ≤ 2m)
Bending Moment (clockwise negative)
Mx = -15x

At x = 0;
M_G = 0 KNm

At x = 2m
M_F^R = -15(2) = – 30 KNm

Shear Force
Q_G^L – Q_F^R = 15 KN (downward force is positive when coming from the right)

Axial Force
No axial force in the member

Final Internal Stresses Diagram

To download this calculation sheet in printable PDF format for free, click HERE
For more structural analysis and design works, continue to visit;

www.structville.com

Like us www.facebook.com/structville

Structural Analysis and Design of Residential Buildings Using Staad.Pro, Orion, and Manual Calculations

By

Ubani Obinna Uzodimma

-

May 13, 2022

This should be a long post, but I am going to try and keep it as brief as possible. This post is more like an excerpt from the publication ‘Structural Analysis and Design of Residential Buildings using Staad Pro V8i, CSC Orion, and Manual calculations’. Here, we are going to briefly present some practical analysis and design of some reinforced concrete elements using Staad Pro software, Orion software, and manual calculations. Ultimately, we are going to make some comparisons of the results obtained based on the different methods adopted in the analysis and design. To learn how to model, design, and detail buildings from the scratch using Staad Pro, Orion, and manual methods, see the link at the end of this post.

To show how this is done, simplified architectural floor plans, elevations, and sections, for a residential two-storey building have been shown below for the purpose of structural analysis and design (see the pictures below).

The first step in the design of buildings is the preparation of the ‘general arrangement’, popularly called the G.A. The G.A. is a drawing that shows the disposition of the structural elements such as the slabs and their types, the floor beams, the columns, and their interaction at the floor level under consideration. For the architectural drawings above, the adopted G.A. is shown in Figure 7. below. There are no spelt out rules about how to prepare G.A. from architectural drawings, but there are basic guidelines that can guide someone on how to prepare a buildable and structurally efficient G.A.

New%2BPicture%2B%25284%2529 — Fig.7: General Arrangement

Design data:
F_ck = 25 N/mm², F_yk = 460 N/mm², C_nom (slabs) = 25mm, C_nom (beams and columns) = 35mm, C_nom (foundations) = 50mm
Thickness of slab = 150mm; Dimension of floor beams = 450mm x 230mm; Dimension of columns = (230 x 230mm)

DESIGN OF THE FLOOR SLABS
PANEL 1: MANUAL ANALYSIS

The floor slab (PANEL 1) is spanning in two directions since the ratio (k) of the longer side (Ly) to the shorter side (Lx) is less than 2.
Hence, k = Ly/Lx = 3.825/3.625 = 1.055 (say 1.1)

Moment coefficients (α) for two adjacent edges discontinuous (pick from table);
Short Span
Mid-span = 0.042
Continuous edge = 0.056
Long Span
Mid-span = 0.034
Continuous edge = 0.045

Design of short span
Mid span
M = αnLx² = 0.042 × 10.9575 × 3.6252 = 6.0475 KN.m
M_Ed = 6.0475 KNm
Effective Depth (d) = h – Cc – ϕ/2
Assuming ϕ12mm bars will be employed for the construction
d = 150 – 25 – 6 = 119mm; b = 1000mm (designing per unit width)

k = M_Ed/(f_ckbd² )
= (6.0475 × 10⁶)/(25 × 1000 × 119² ) = 0.0171
Since k < 0.167 No compression reinforcement required
z = d[0.5+ √(0.25 – 0.882k)] = z = d[0.5+ √(0.25 – (0.882 × 0.0273)] = 0.95d
A_s1 = M_Ed/(0.87f_yk z)
A_s1= (6.0475 × 10⁶)/(0.87 × 460 × 0.95 × 119) = 133.668 mm²/m
Provide Y12mm @ 250mm c/c BOT (A_Sprov = 452 mm²/m)

A little consideration will show that this provided area of steel will satisfy serviceability limit state requirements. To see how to carry out deflections and crack control verifications, see the the link at the bottom of this post.

Result from Orion showing the Short Span (mid span) design moments (Wood and Armer effects inclusive) (PANEL 1)

Result from Staad showing the Short Span (mid span) design moments (Wood and Armer effects inclusive) (PANEL 1)

A little observation will show that the design moment values from the different methods are very similar. The full detailing of the floor slabs is as shown below.

Figure 9: Bottom Reinforcement Detailing

Figure 10: Top Reinforcement Detailing

Figure 11: Section of the floor slab

DESIGN OF THE BEAMS
Let us take Beam No 1 from our GA as a design case study:
The loading of the beam has been carried out as shown below. The beam is primarily subjected to load from the slab, the weight of wall, and its own self-weight. To see how to manually calculate the loading on beams, follow the link at the end of the post.

The internal forces from the loading is as shown below;

The internal forces from Orion software for Beam No 1 is as shown below. Load decomposition using finite element analysis was used for the load transfer.

The internal forces from Staad software for Beam No 1 is as shown below.

A_s1 = M_Ed/(0.87f_ykz)
= (36.66 × 10⁶)/(0.87 × 460 × 0.95 × 399) = 241.667 mm²
Provide 2Y16 mm BOT (A_Sprov = 402 mm²)
The detailing of Beam No 1 is as shown below;

DESIGN OF THE COLUMNS
Loads from slabs and beams are transferred to the foundations through the columns. In typical cases, columns are usually rectangular or circular in shape. Normally, they are usually classified as short or slender depending on their slenderness ratio, and this, in turn, influences their mode of failure. Columns are either subjected to axial, uniaxial, or biaxial loads depending on the location and/or loading condition. Eurocode 2 demands that we include the effects of imperfections in the structural design of columns. The design of columns is covered in section 5.8 of EC2.

The column axial loads have been obtained by summing up the reactions from all the beams supported by the columns, including the self weight of the column.

Let us use column A1 as example.

At the roof level, the column is supporting beam No 2 (Support Reaction V₁ = 13.27 KN) and Beam No 3 (Support Reaction V_A = 12.99 KN). At the first floor level (see Analysis and Design of Beam No 1 and 2), the column is supporting Beam No 1 (Support Reaction V₁ = 41.38 KN), and Beam No 2 (Support Reaction V_A = 42.49 KN). Therefore the summation of all these loads gives the axial load transferred from the beams. For intermediate supports, note that the summation of the shear forces at the support gives the total support reaction (neglect the signs and use absolute value. Another method of calculating Column Axial Load is by Tributary Area Method. This method has not been adopted in this work.

COLUMN A1
Total Columns Self weight = 12.14 KN
Load from roof beams = 13.27 + 12.99 = 26.26 KN
Load from floor beams = 46.21 + 42.49 = 88.70 KN
Total = 127.13 KN

Axial Load from Orion (A1) = 126.6 KN
Axial Load from Staad (A1) = 130.684 KN

COLUMN A3
Total Columns Self weight = 12.14 KN
Load from roof beams = 35.41 + 11.46 = 46.87 KN
Load from floor beams = 105.33 + 60.85 = 166.18 KN
Total = 225.19 KN

Axial Load from Orion (A3) = 202.3 KN
Axial Load from Staad (A3) = 201.632 KN

COLUMN A5
Total Columns Self weight = 12.14 KN
Load from roof beams = 17.19 + 5.70 = 22.89 KN
Load from floor beams = 83.64 + 37.91 = 121.55 KN
Total = 156.58 KN

Axial Load from Orion (A5) = 155.9 KN
Axial Load from Staad (A5) = 163.207 KN

COLUMN A7
Total Columns Self weight = 12.14 KN
Load from roof beams = 43.15 + 9.48 = 52.63 KN
Load from floor beams = 38.26 + 62.45 = 100.71 KN
Total = 165.48 KN

Axial Load from Orion (A7) = 133.9 KN
Axial Load from Staad (A7) = 140.392 KN

As you can see, for design purposes, the axial loads from the three methods are very comparable. To see how to obtain the column design moments from the use of sub-frames, follow the link at the end of the post.

Design of Column E5
Reading from chart; d₂/h = 0.2;
M_Ed/(f_ck bh² )
= (10.002 × 10⁶)/(25 × 230 × 230² ) = 0.03288
N_Ed/(f_ckbh)
= (399.88 × 10³)/(25 ×230 × 230) = 0.302
From the chart:
(A_sF_yk)/(bhf_ck ) = 0.05
Area of longitudinal steel required (As) = (0.05 × 25 × 230 × 230)/460 = 143.75 mm²
A_s,min = 0.10 NEd/fyd
= (0.1 × 399.887)/400 = 0.099 mm² < 0.002 × 230 × 230 = 105.8 mm²
Provide 4Y16mm (Asprov = 804 mm²)

Links
Minimum size = 0.25ϕ = 0.25 × 16 = 4mm < 6mm
We are adopting Y8mm as links
Spacing adopted = 200mm less than min{b, h, 20ϕ, 400mm}

Result from Orion for column E5

Result from Staad for column E5

Staad Provided Y8@225mm links
The column detailing is as shown below;

DESIGN OF FOUNDATIONS
All loads from the superstructure of a building are transferred to the ground. If the foundation of a building is poorly designed, then all the efforts input in designing the superstructure is in vain. It is therefore imperative that adequate care is taken in the design of foundations. Foundation design starts with a detailed field and soil investigation. It is very important to know the index and geotechnical properties of the soil, including the soil chemistry, so that the performance of the foundation can be guaranteed.

Analysis and Design of footing E8

Bearing Capacity of the foundation = 150 KN/m²;

Effective depth
Concrete cover = 50mm
AssumingY12mm bars,
d = 400 – 50 – 6 = 344mm
The ultimate limit state design moment can be obtained by considering the figure below;

k = M_Ed/(f_ck bd²)
= (37.518 × 10⁶)/(25 × 1000 × 344² ) = 0.01268 (designing per metre strip)
Since k < 0.167 No compression reinforcement required
z = d[0.5+ √(0.25 – 0.882k)] = z = d[0.5+ √(0.25 – (0.882 × 0.0273)] = 0.95d
A_s1 = M_Ed/(0.87f_ykz)
= (37.518 × 10⁶)/(0.87 × 460 × 0.95 × 344) = 286.869 mm²/m

To calculate the minimum area of steel required;
f_ctm = 0.3 × (f_ck)^(2⁄3) = 0.3 × 25 ^(2⁄3) = 2.5649 N/mm² (Table 3.1 EC2)
A_Smin = 0.26 × f_ctm/F_yk × b × d = 0.26 × 2.5649/460 ×1000 × 344 = 498.7 mm²
Check if A_Smin < 0.0013 × b × d (447.2 mm²)
Since, A_Smin = 498.7 mm², the provided reinforcement is adequate.
Provide Y12 @ 200mm c/c (A_Sprov = 565 mm²/m) each way

Shear at the column face
Ultimate Load on footing from column = 399.887 kN
Design shear stress at the column perimeter v_Ed = βV_Ed/(u₀d)
β is the eccentricity factor (see section 6.4.3 of EC2)
β = 1+ 1.8√[(16.48/230)²+(8.99/230)²] = 1.146
Where u_o is the column perimeter and d is the effective depth
v_Ed = βV_Ed/(u₀d)
= (1.15 × 399.887 × 10³)/(4(230) × 344) = 1.452N/mm²
V_Rd,max = 0.5vf_cd
v = 0.6[1 – (f_ck/250) ] = 0.6[1 – (25/250) ] = 0.54 N/mm²
f_cd = (α_cc f_ck)/γ_c = (0.85 × 25)/1.5 = 14.167 N/mm²
V_Rd,max = 0.5 × 0.54 × 14.167 = 3.825 N/mm²v_Ed < V_Rd,max. This is very ok

Transverse shear at ‘d’ from the face of column

Width of shaded area = a – d = 0.635 – 0.344 = 0.291m
Area of shaded area = (1.5m × 0.291m) = 0.4365 m²
Therefore, ΔV_Ed = (189.386 + 175.939)/2 × 0.4365 m² = 79.077 KN
v_Ed = V_Ed/bd = (79.077 × 10³)/(1500 × 344) = 0.15325 N/mm²
V_Rd,c = [C_Rd,c k (100ρ₁ f_ck )^(1/3) + k¹.σ^cp] × (2d/a) ≥ (V_min + k₁.σ,sub>cp) bw.d
C_Rd,c = 0.18/γ_c = 0.18/1.5 = 0.12
k = 1 + √(200/d) = 1+√(200/344) = 1.7624 > 2.0, therefore, k = 1.7624
V_min = 0.035k^(3/2) f_ck^(1/2)
V_min = 0.035 × (1.7624)^(3/2) × (25)^(1/2) = 0.4094 N/mm²
ρ₁ = As/bd = 565/(1000 × 344) = 0.001642 < 0.02;
V_Rd,c = [0.12 × 1.7624 (100 × 0.001642 ×25 )^(1/3) ] = 0.3386 N/mm² × (2d/a) < V_min
But in this case, d = a
Hence, V_Rd,c = 2 × 0.3386 = 0.6772 N/mm²
Since V_Rd,c (0.6772) > V_Ed (0.1503 KN), No shear reinforcement is required.

Punching Shear at 2d from the face of column
Punching shear lies outside the footing dimensions. No further check required.

Design Result from Orion

The detailing of the footing is as shown below;

The structural analysis and design of all members have been fully done, including a step by step tutorial on how to model and design on Orion and Staad Pro, and how to manually design. See the completed models below;

New%2BPicture%2B%252836%2529 — Fully completed model on Orion

New%2BPicture%2B%252837%2529 — Fully completed model on Staad Pro

To download the simplified e-book where all the members have been designed and completely detailed, including bar bending schedule and quantification of materials, click HERE.

Thank you, and God bless you.

Free MATLAB Code for Flexural Design of R.C. Sections According to EC2

Two Approaches to the Calculation of Deflection in Eurocode 2

Shear Deformation of Beams Using Virtual Work Method

Example 1: Shear deflection of a simply supported beam carrying a uniformly distributed load

Example 2: Shear deformation of a simply supported beam carrying a concentrated load at the mid-span.

Example 3: Shear deformation of Cantilever beam carrying a uniformly distributed load

Elastic Settlement of Shallow Foundations

Worked Example

Analysis of Three-Hinged Arch Structures

Solved Example on Analysis of a Three-hinged Arch

Deflection of Statically Indeterminate Frames

Blast Resistant Structures: 21 Things You Should Know

Application of Finite Difference Method to the Elastic Analysis of Simply Supported Thin Plates

Finite Difference Method of Analysis of Thin Plates

Example on the Analysis of Statically Determinate Frames (Part 2)

Structural Analysis and Design of Residential Buildings Using Staad.Pro, Orion, and Manual Calculations

EDITOR PICKS

POPULAR POSTS

Structural Analysis and Design of Residential Buildings Using Staad.Pro, Orion, and Manual Calculations

How to Calculate the Number of Blocks Required to Complete a 3 Bedroom Flat

Can you identify the cause of failure of this building?

POPULAR CATEGORY

ABOUT US

FOLLOW US