Types of Floor Systems for Steel Framed Buildings

By

-

July 27, 2020

Table of Contents

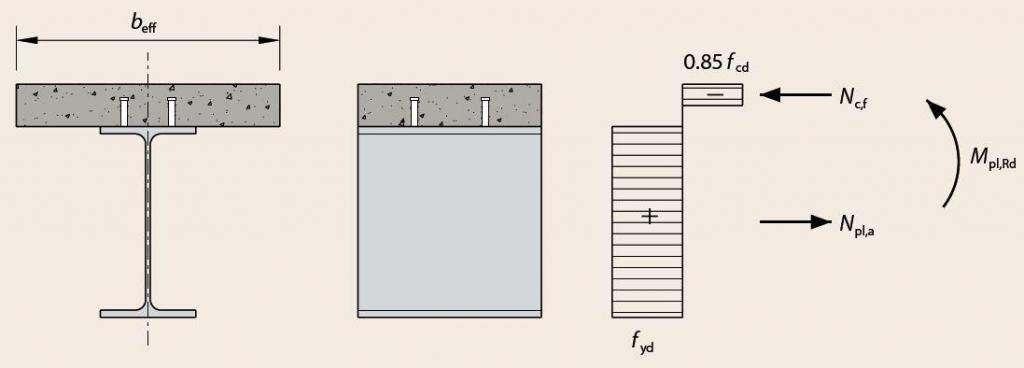
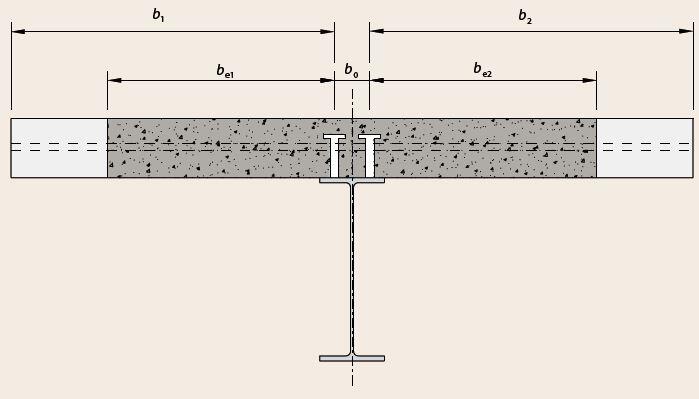
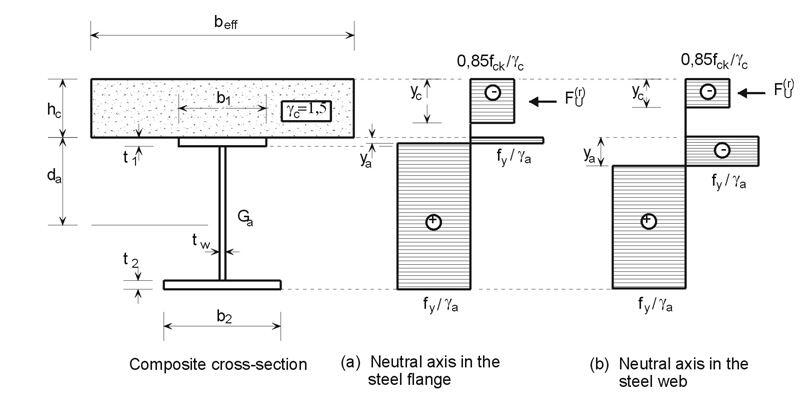
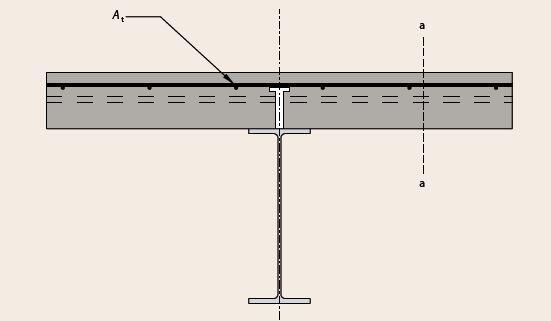
Floors in buildings have a primary function of carrying loads and supporting the activities of the occupants. In addition to carrying loads, floors in buildings also provide the needed rigid diaphragm action for transmitting horizontal loads to the stabilising vertical components. Furthermore, floors also support additional superimposed loads such as ceilings, building services, and finishes such as screeds and tiles.

composite slab supporting building services — Composite slab supporting building services

The types of floor systems that used in steel-framed buildings are;

Short-span composite beams and composite slabs with metal decking.
Slimdek^®.
Cellular composite beams with composite slabs and steel decking.
Slimflor^® beams with precast concrete units.
Long-span composite beams and composite slabs with metal decking.
Composite beams with precast concrete units.
Non-composite beams with precast concrete units.

Short span composite beam and composite slab with metal decking

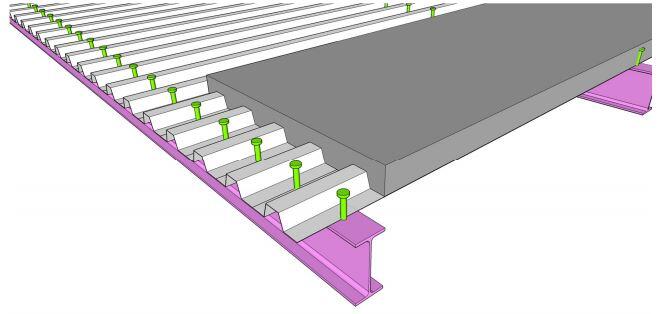
In this floor system, shear connectors are welded through the metal decking to the top flange of downstand beams to enable it act compositely with an in-situ composite slab. For short span floor systems, the secondary beams are typically spaced between 3 – 4m and are supported by the primary beams. The primary and secondary beams act compositely with the composite slab, but the edge beams are usually non-composite. At 3-4m spacing, secondary beams will span about 6 – 7.5m when positioned orthogonally to the slab, while the primary beams will span about 6-9m (positioned parallel to the slab).

short span composite slab section — Short span composite decking

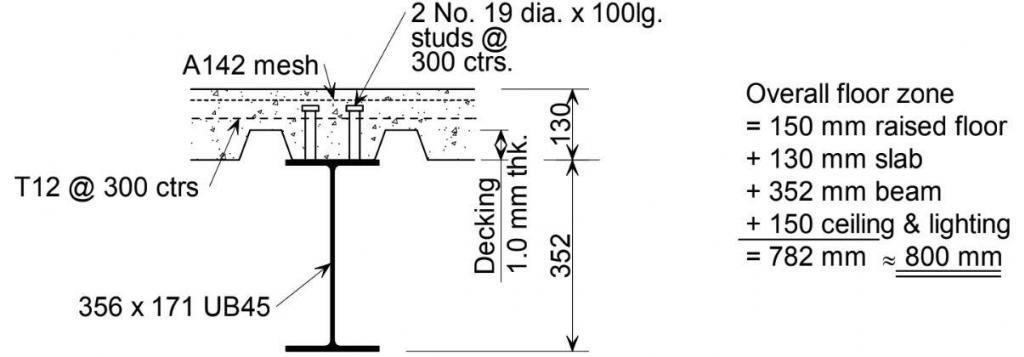
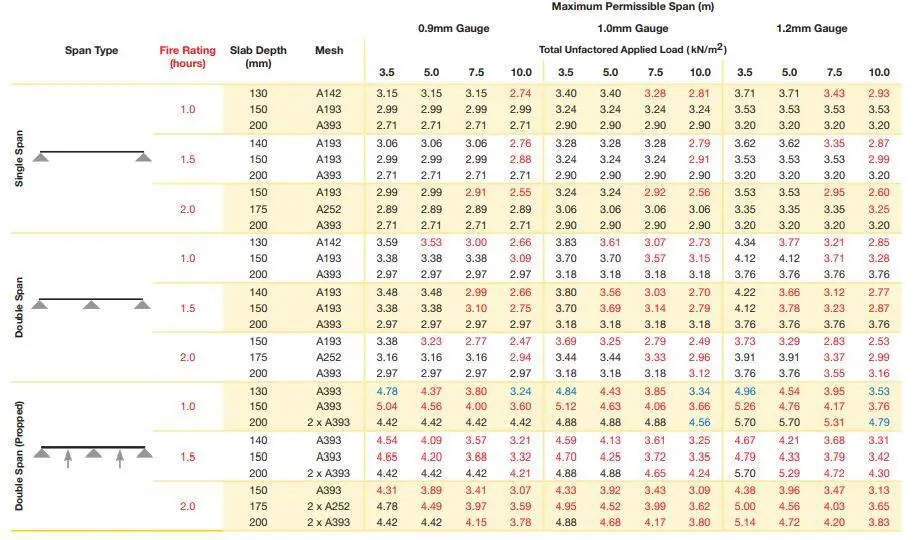
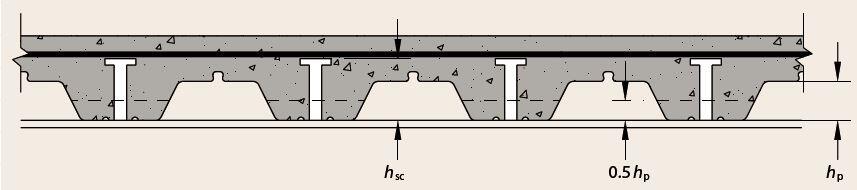
The floor slab consists of composite profiled metal decking with a typical depth of about 130 mm thick with in-situ concrete topping. The profiles may be re-entrant decking or trapezoidal. Re-entrant decking uses more concrete than trapezoidal decking, but has increased fire resistance for a given slab depth. Trapezoidal decking generally spans further than re-entrant decking, but the shear stud resistance is less with trapezoidal decking than with re-entrant decking. The profiles are usually between 0.5 to 1.2mm thick.

rentrant decking — Re-entrant profile composite decking

trapezoidal composite decking — Trapezoidal profile composite decking

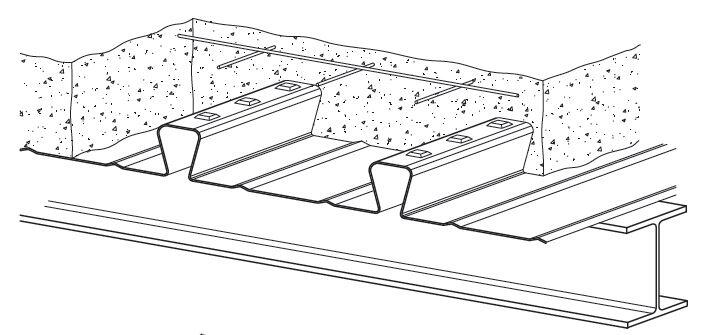
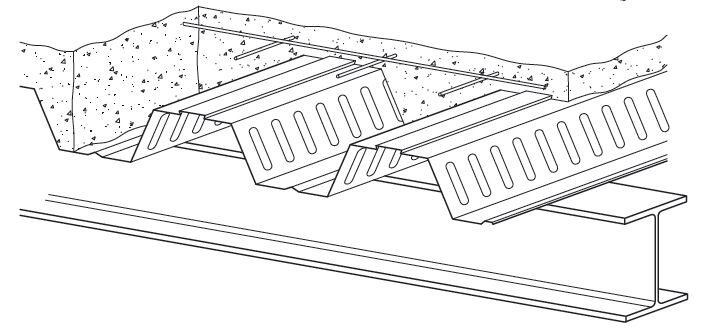
Mesh reinforcement is provided at the top of the slab to help reduce cracking, spread localised loads, enhance fire resistance, and act as shear reinforcement around the shear connectors. The decking is normally designed to support the wet weight of the concrete and construction loading as a continuous member over at least two spans, but the composite slab is normally designed as simply supported between beams (but some continuity reinforcement is required). The design of the decking is usually picked from the manufacturer’s technical data sheet.

Advantages
(1) Shallower beams than non-composite floors
(2) More economical
(3) Light weight

Disadvantages
(1) More columns needed than with long-span systems.
(2) Deeper overall floor zone than shallow floor systems.
(3) Generally, beams require fire protection.

Slimdek

Slimdek is a shallow floor system comprising asymmetric floor beams (ASBs) supporting heavily ribbed composite slabs with 225 mm deep decking. ASBs are proprietary beams with a wider bottom flange than top. The section has embossments rolled into the top flange and acts compositely with the floor slab without the need for additional shear connectors.

The decking spans between the bottom flanges of the beams and acts as permanent formwork to support the slab and other loads during construction. The in-situ concrete acts compositely with the decking and encases the beams so that they lie within the slab depth – apart from the exposed bottom flange. The floor normally spans between 6 – 9m grid with floor depth of about 280 – 350 mm. Reinforcements of 16mm to 25mm bars are placed in the ribs of the slab to improve strength in the fire condition, while mesh reinforcement is paced above ASB.

Advantages
(1) Shallow floor zone – reduction in overall building height and cladding.
(2) Virtually flat soffit allows easy service installation and offers flexibility of internal wall positions.

Disadvantages
(1) Steel weight is often greater than other floor systems.
(2) Connections require careful detailing due to the width of the bottom flange.

Cellular composite beams with composite slabs and steel decking

Cellular beams are beams with openings at short regular intervals along their length. The beams are either fabricated from 3 plates or made from rolled sections. Openings, or ‘cells’, are normally circular, which are ideally suited to circular ducts, but can be elongated, rectangular or hexagonal. Cells may have to be filled in to create a solid web at positions of high shear, such as at supports or either side of point loads along the beam.

cellular beam composite slab — Cellular beam composite slab construction

Cellular beams can be arranged as long-span secondary beams, supporting the floor slab directly, or as long-span primary beams which are aligned parallel to the span of the slab supporting other cellular beams or conventional rolled section secondary beams. The secondary beams are typically placed at 3 – 4 m spacing, supported by primary beams on a 6 m, 7.5 m or 9 m column grid. The decking and slab can be designed using decking manufacturer’s design tables or software.

Advantages
Long, column-free floor spans.
Relatively lightweight beams compared with other long-span systems.
Economic long-span solution.
Precamber can be accommodated during the fabrication of the members.
Regular openings in the web allow ducts and other services to pass through the beams.

Disadvantages
Increased fabrication costs compared with plain sections.

Slimflor^® beams with precast concrete units

In slim floor system where the beams are contained within the structural floor depth. A steel plate (typically 15 mm thick) is welded to the underside of a UC section to make the Slimflor beam. This plate extends beyond the bottom flange by 100 mm either side, and supports the precast floor units. A structural concrete topping with reinforcement is recommended to tie the units together and the topping thickness should cover the units by at least 30 mm.

slimfloor section — Typical slimflor arrangement

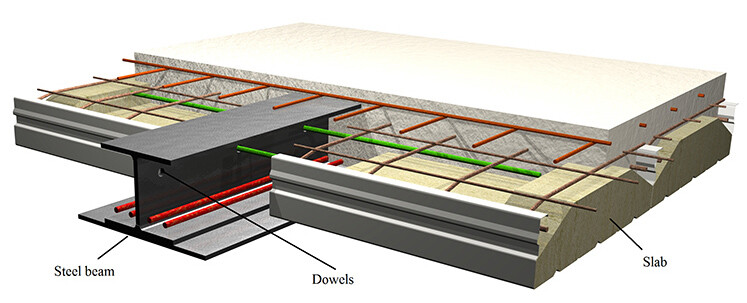
A composite Slimflor beam can be achieved by welding shear connectors (normally 19 mm diameter by 70 mm long) to the top flange of the UC. Reinforcement is then placed across the flange into slots prepared in the precast units, or on top of shallow precast units. If the steel beams are to be designed compositely, the topping should cover the shear connectors by at least 15 mm, and the precast units by 50 mm.

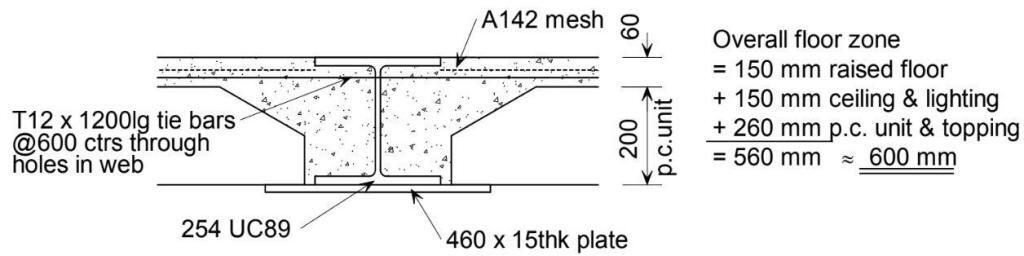
Only 152 UCs and 203 UCs are normally suitable as composite beams because the overall depth of the floor slab becomes impractical for larger serial sizes. Precast units are usually cambered to cancel out dead load deflections between beams, and the floor spans are typically between 4.5m to 7.5m even though spans of 10m can be achieved.

Advantages
(1) Beams normally require no fire protection for up to 60 minutes fire protection.
(2) Shallow floor zone – reduction in overall building height and cladding. Virtually flat soffit allows easy service installation and offers flexibility of internal wall positions.
(3) Shear connectors can be welded off-site, enabling larger stud diameters to be used and reducing site operations.

Disadvantages
(1) The steelwork is relatively heavy.
(2) Extra fabrication is involved in welding the plate to the UC. Connections require more detailing as the plate is wider than the column.
(3) Precast units involve more individual lifting operations than decking, which is delivered and erected in bundles. The erection sequence requires access for installation of the concrete units.

Long-span composite beams and composite slabs with metal decking

This system consists of composite beams using rolled steel sections supporting a composite slab in a long-span arrangement of, typically, 10 to 15 m. Grids are either arranged with long-span secondary beams at 3 m to 4 m spacing supporting the slab, supported by short-span primary beams, or with short- span secondary beams (6-9 m span) supported by long-span primary beams.

long span cellular beam — Long span composite cellular beam floor

The depth of the long-span beams means that service openings, if required, are provided within the web of the beam. Openings can be circular, elongated or rectangular in shape, and can be up to 70% of the beam depth. They can have a length/depth ratio of up to 2.5. Web stiffeners may be required around holes. Shear studs are normally positioned in pairs, with reinforcing bars placed transversely across the beams to act as longitudinal shear reinforcement.

Advantages
(1) Large column-free areas.
(2) Service ducts pass through openings in the web of the beams

Disadvantages
(1) Deeper floor zones.
(2) Heavier steelwork than some short-span solutions.
(3) Fire protection required for 60 minutes fire resistance and above.

Composite beams with precast units

This system consists of rolled steel beams with shear studs welded to the top flange. The beams support precast concrete units with a structural concrete infill over the beam between the ends of the units, and often with an additional topping covering the units. The precast units are either hollow core, normally 150 – 260 mm deep, or they are solid planks of 75 mm to 100 mm depth.

composite beam with precast units — Different configurations if composite floors with precast units

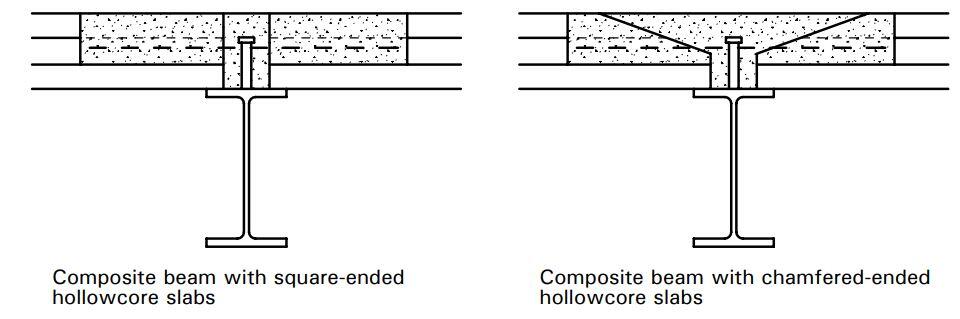
The shear studs and transverse reinforcement allow the transfer of the longitudinal shear force from the steel section into the precast units and the concrete topping, so that they can act together compositely. Composite design is not permitted unless the shear connectors are situated in an end gap (between the concrete units) of at least 50 mm. Minimum flange widths are crucial for providing a safe bearing for the precast units and room for the shear studs.

Advantages
(1) Fewer secondary beams, due to long-span precast units.
(2) Shear connectors for most beams can be welded off site, enabling larger stud diameters to be used and fewer site operations. It is usually convenient to weld studs to edge beams on site.

Disadvantages
(1) The beams are subject to torsion and may need stabilising during the construction stage.
(2) The precast units need careful detailing for adequate concrete encasement of shear connectors and installation of transverse reinforcement.
(3) More individual lifting operations compared to the erection of decking, and the erection sequence requires access for installation of the concrete units.

Non-composite beams with precast units

This system consists of rolled steel beams supporting precast concrete units. The precast units may be supported on the top flange of the steel beams, or, to reduce construction depth, supported on ‘shelf’ angles. Shelf angles are bolted or welded to the beam web, with an outstand leg long enough to provide adequate bearing of the precast units and to aid positioning of the units during erection. Precast concrete units are generally grouted in position. The units may have a screed (which may be structural), or may have a raised floor. The precast units are either hollow core, normally 150-260 mm deep, or they are solid planks of 75 mm to 100 mm depth.

precast beam and slab in non composite construction — Floor construction with precast concrete units in non-composite construction

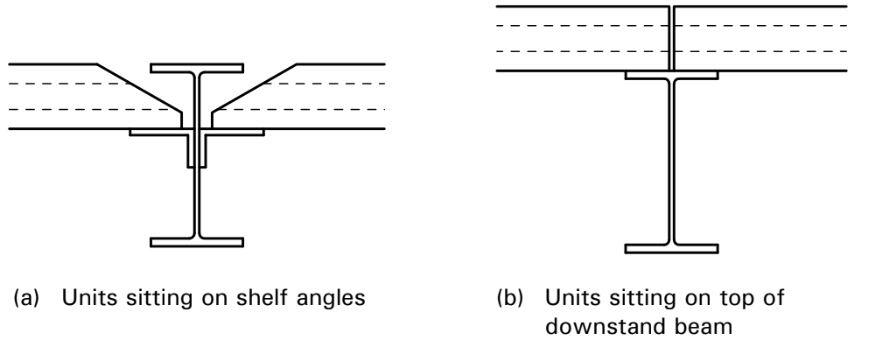
In order to meet robustness requirements, mesh and a structural topping may be required, or reinforcement concreted into hollow cores and passed through holes in the steel beam web. Tying may also be required between the concrete units and the edge beams.

Advantages
(1) Fewer secondary beams, due to long-span precast units.
(2) A simple solution involving basic member design.

Disadvantages
The beams are subject to torsion and may need stabilising during the construction stage.
More individual lifting operations compared with the erection of decking, and the erection sequence requires access for installation of the concrete units.

Source:
Brown D.G., Iles D.C., Yandzio E. (2009): Steel building design: Medium rise braced frames (In accordance with Eurocodes and the UK National Annexes). The Steel Construction Institute, UK

Second-Order Effects in Steel Structures

By

Ubani Obinna

-

July 25, 2020

Second-order effects involve the analysis of a structure based on the deformed geometry. In other words, second-order analysis recognizes the deflection in a structure due to an externally applied load, and determines its effect on the internal forces generated thereof. The magnitude at which the internal forces in a structure increase due to second-order effects depend on the geometry, stiffness, and support conditions of the structure. This is usually employed in the verification of the stability of steel structures against phenomena such as buckling.

The sensitivity of a frame to second order effects may be illustrated simply by considering one ‘bay’ of a multi-storey building in simple construction (i.e. with pinned connections between beams and columns); the bay is restrained laterally by a spring representing the bracing system. First and second order displacements are illustrated below.

first and second order effects in a pinned braced frame 1

For first order effects;
kδ₁ = H₁

For second order effects;
kδ₂= H₁ +V(δ₂ / h) = H₂

On rearranging the equation for second order effects, the equilibrium condition can be expressed as;

H₂ = H₁[1 / (1 – V/kh)]

Hence, it can be observed that if the stiffness of the structure k is large, there will be little amplification of the horizontal force, and first order analysis will be adequate for the structure. On the other hand, if the value of vertical force tends toward a critical value V_cr (= kh) then displacements and forces in the restraint tend toward infinity. The ratio V_cr/V, which may be expressed as a parameter α_cr, is thus an indication of the second order amplification of displacements and forces in the bracing system due to second order effects.

The amplifier is given by:

[1/(1 – 1/α_cr)

This amplification factor applies to horizontal forces such as wind loads and imperfection loads.

Criteria for considering second order effects

According to BS EN 1993-1-1, 5.2.1(2), the effects of the deformed geometry of the structure (second order effects) need to be considered if the deformation significantly increase the forces in the structure or if the deformations significantly modify structural behaviour. For elastic global analysis, clause 5.2.1 says that the second order effects are significant if the parameter α_cr < 10, where α_cr is determined by first order analysis and for a braced frame is defined by the approximate expression:

α_cr = (H_Ed/V_Ed) x (h/δ_h,Ed)

where:
H_Ed is the design value of the horizontal reaction at the bottom of the storey to the horizontal loads and the equivalent horizontal forces1
V_Ed is the total design vertical force on the structure on the bottom of the storey
δ_h,Ed is the horizontal displacement at the top of the storey, relative to the bottom of the storey, when the frame is loaded with horizontal loads (e.g. wind) and equivalent horizontal forces which are applied at each floor level
h is the storey height.

Methods for determining second order effects

Where second order effects need to be evaluated, BS EN 1993-1-1, 5.2.2 says that they may be allowed for by:

An appropriate second-order analysis, taking into account the influence of the deformation of the structure.
Using appropriate (increased) buckling lengths of members
Amplification of an elastic first order analysis using the initial geometry of the structure.

Second Order Analysis

A range of second order analysis software is available. Use of any software will give results that are to some extent approximate, depending on the solution method employed, the types of second-order effects considered and the modelling assumptions. Generally, second-order software will automatically allow for frame imperfections, so the designer will not need to calculate and apply the equivalent horizontal forces. The effects of deformed geometry (second-order effects) will be allowed for in the analysis. The effect of member imperfections and such things as residual stresses are allowed for if verifying members in accordance with the rules in Section 6 of BS EN 1993-1-1.

Use of increased column buckling length

The use of increased column buckling effective lengths is generally not recommended, simply because of the manual effort involved in calculating the effective length factors. However, if this option is chosen, effective length factors can be determined using a source of non-conflicting complementary information (NCCI), such as BS 5950 Annex E or DD ENV 1993-1-1 Annex E.

Amplification of first order effects

Use of amplified first order effects is subject to the limitation that α_cr ≥ 3 (if α_cr is less than 3, second order analysis must be used). The amplifier is given by:

[1/(1 – 1/α_cr)

Only the effects due to the horizontal forces (including the equivalent horizontal forces) need to be amplified. In a braced frame, where the beam to column connections are pinned and thus do not contribute to lateral stiffness, the only effects to be amplified are the axial forces in the bracing members and the forces in columns that are due to their function as part of the bracing system.

Vibration Serviceability of Composite Slabs

By

Ubani Obinna

-

July 20, 2020

Vibration analysis of floors is not entirely new in the field of structural engineering. Numerous studies and researches have been devoted to human-structure interaction, with emphasis on human perception of vibration in civil engineering structures. Recently, the quest for construction of slender structures with large unobstructed areas (with flexible partitioning) has made the idea of vibration serviceability very important in the design of structures. Once a building is constructed, it is usually challenging to ameliorate vibration issues since it involves modifying the mass and stiffness of the structure.

In the UK, the vibration sensitivity of composite slabs has been traditionally checked by ensuring that the vertical natural frequency of secondary and primary beams is greater than 4Hz. However, a new approach has been recommended in the publication SCI P354 (2009) for checking the vibration serviceability of composite slabs. An example using the approach has been presented in this article.

In P354, two modes of vibration have been recommended for checking acceptability. In mode A, alternate secondary spans may be deflecting up and down (assuming simply supported conditions) with the participation of the slabs (as fixed ended) but not the primary beams. The primary beams are assumed to form nodal lines with zero deflection. In mode B, the primary beams may be deflecting in the same manner, but the secondary beams and slabs which are effectively fixed ended contribute to extra deflection. Therefore for mode B, the deflection is a sum of three contributions. The lower frequency of the two modes is taken as the fundamental frequency and should be at least 3Hz to ensure that walking activities will be outside the frequency zone that will cause resonance.

The design procedures for determining the dynamic performance of composite floors is as follows;

Determine the natural frequency
Determine the modal mass of the floor
Evaluate the response of the floor
Verify the response of the floor against the requirements

Solved Example

The figure below shows a part plan of a composite floor. The slab is to be constructed using profiled metal decking and normal weight, grade 30 concrete. The longitudinal beams are of grade S275 steel with a span of 7.5 m and spaced 3 m apart. Check the acceptance of the floor for vibration. 406 x 178 x 67 UKB as the internal beams. T

Member Geometry

Primary beams 610 x 229 x 140 UKB
Secondary beams 406 x 178 x 67 UKB

Beam span = 7.5 m
Beam spacing = 3.0 m
Total depth of slab h_s = 130 mm
Depth of profile h_p = 60 mm
Overall height of profile h_d= 72 mm
Depth of concrete above profile = 58 mm
Profile: SMD TR60⁺ (1.2 mm gauge)
Gauge = 1.2 mm
Mesh: A142

Floor loading
130 mm deep concrete slab = 2.21 kN/m² (manufacturer’s data)
Self weight of profile decking = 0.131 kN/m²
Ceiling and services = 1 kN/m²
Finishes = 1.2 kN/m²
10% Imposed = (0.1 x 5 kN/m²)= 0.5 kN/m²
Sub total = 5.041 kN/m²

Primary beams = (140 kg/m x 9.81/7.5) x 10^-3 = 0.183 kN/m²
Scondary beams = (67 kg/m x 9.81/3) x 10^-3 = 0.22 kN/m²
Total = 5.44 kN/m² = (5.44 x 10³)/9.81 = 554.54 kg/m²

Typical SMD TR60+ profile

Calculation of composite slab properties

Profile neutral axis = 33.7 mm
Profile area/unit width = 1633 mm²/m
Profile moment of inertia = 119.8 cm⁴/m
Height of re-entrant rib = 60 mm

Concrete area/unit width for 130 mm thick slab= 0.096 m²/m
Therefore effective slab thickness = 96 mm

For dynamic properties, take the gross uncracked moment of inertia. Dynamic modulus of elasticity of concrete E_cm = 38 kN/mm².

Modular ratio α = E_s/E_cm = 210/38 = 5.526

We can calculate the elastic neutral axis of the composite slab from the table below.

Section	Area A (cm²)	Neutral axis y (cm)	Area x y (cm³)
Concrete	960/α = 173.724	9.6/2 = 4.8	816.5
Profile	16.33	13 – 3.37 = 9.63	157.257
Total	∑A = 190.054		∑Ay = 973.757

Elastic neutral axis of the composite slab NA = ∑Ay/∑A = 973.757/190.054 = 5.123 cm below the top of the slab

The moment of inertia of the composite slab can be calculated from the table below;

Section	Distance from NA (cm)	Area x Distance² (cm⁴)	I_y,local (cm⁴)
Concrete	0.323	18.124	3139
Profile	4.507	331.712	119.8
		349.836	3258.8

Second moment of area of composite slab = 349.836 + 3258.8 = 3608.636 cm⁴ (36.0863 x 10^-6 m⁴)

Moment of inertia of the composite secondary beam

406 x 178 x 67 UKB
Span = 7.5m; Weight = 67.1 kg/m
Depth = 409.4 mm; Area = 85.5 cm²
I_y = 24300 cm⁴; Effective breadth b_eff = 1875 mm

Composite section properties

Section	Width (cm)	Depth (cm)	y (cm)	A (cm²)	Ay (cm³)	Ay² (cm⁴)	I_local
Slab	187.5	7.0	3.50	1312.5/5.526 = 237.513	831.297	2909.532	969.847
Beam			33.47	85.5	2861.68	95780.596	24300
				∑A = 323.013	∑Ay = 3692.977	∑Ay² = 98690.128	∑I_local = 25269.847

Position of elastic neutral axis = ∑Ay/∑A = 3692.977/323.013 = 11.432 cm from the top of the slab

Gross moment of area = 98690.128 + 25269.847 – (11.432²x 323.013) = 81745.204 cm⁴ (8.1745 x 10^-4 m⁴)

Moment of inertia of the composite primary beam

610 x 229 x 140 UKB
Span = 6.0m; Weight = 139.9 kg/m
Depth = 617.2 mm; Area = 178 cm²
I_y = 112000 cm⁴; Effective breadth b_eff = 1500 mm

Composite section properties

Section	Width (cm)	Depth (cm)	y (cm)	A (cm²)	Ay (cm³)	Ay² (cm⁴)	I_local
Slab	150	9.6	4.8	1440/5.526 = 260.586	1250.81	6003.9	2001.3
Beam			43.86	178	7807.08	342418.53	112000
				∑A = 438.586	∑Ay = 9057.89	∑Ay² = 348422.43	∑I_local = 114001.3

Position of elastic neutral axis = ∑Ay/∑A = 9057.89/438.586 = 20.652 cm from the top of the slab

Gross moment of area = 114001.3 + 348422.43 – (20.652²x 438.586) = 275364.5625 cm⁴ (27.5364 x 10^-4 m⁴)

Fundamental natural frequency

Mode A

(i) Slab – Fixed Ended
w = 5.041 kN/m² x 3 m = 15.123 kN/m
δ₁ = wL³/384EI = (15.123 x 3³)/(384 x 210 x 10⁶ x 36.0863 x 10^-6) = 1.403 x 10^-4m = 0.14 mm

(ii) Secondary beam – Simply Supported
w = (5.041 kN/m² + 0.22 kN/m²) x 3 m = 15.783 kN/m
δ₂ = 5wL⁴/384EI = (5 x 15.123 x 7.5⁴)/(384 x 210 x 10⁶ x 8.1745 x 10^-4) = 3.629 x 10^-3m = 3.629 mm

Total deflection for mode A δ = 0.14 + 3.629 = 3.760 mm

Natural frequency for mode A f_A = 18/√δ = 18/√3.760 = 9.282 Hz

Mode B

(i) Slab – As above

(ii) Secondary beam (assume fixed ended)
w = (5.041 kN/m² + 0.22 kN/m²) x 3 m = 15.783 kN/m
δ₂ = wL⁴/384EI = (15.123 x 7.5⁴)/(384 x 210 x 10⁶ x 8.1745 x 10^-4) = 7.2589 x 10^-4m = 0.725 mm

(iii) Primary beam (assume simply supported)
Reactive force from secondary beam = (15.783 x 7.5)/2 = 59.186 kN
w = (5.041 kN/m² + 0.183 kN/m²) x 3.75 m = 19.59 kN/m

δ₃ = 5wL⁴/384EI + PL³/48EI = [(5 x 19.59 x 6⁴)/(384 x 210 x 10⁶ x 27.5364 x 10^-4)] + [(59.186 x 6³)/(48 x 210 x 10⁶ x 27.5364 x 10^-4)] = (5.716 x 10^-4) + (4.605 x 10^-4) = 1.032 x 10-3 m = 1.032 mm

Therefore total deflection = 0.14 + 0.725 + 1.032 = 1.897 mm

Natural frequency for mode B f_B = 18/√δ = 18/√1.879 = 13.13Hz

Therefore the fundamental frequency of the floor is found in Mode A f₀ = 9.292 Hz > 3.0 Hz (Okay)

Calculation of Modal Mass

The effective floor length can be calculated from;

L_eff = 1.09(1.10)^{n_y – 1}(EI_b/mbf₀²)^1/4 L_eff≤ n_yL_y

Where;
n_y is the number of bays in the secondary beam direction (n_y ≤ 4)
EI_b is the flexural rigidity of the composite secondary beam (expressed in Nm² when m is expressed in kg/m²)
b is the spacing of the secondary beam = 3.0 m
f₀ is the fundamental natural frequency
L_y is the span of the secondary beams

L_eff = 1.09(1.10)^{1 – 1}(210 x 10⁹ x 8.1745 x 10^-4/554.54 x 3 x 9.292²)^1/4 = 7.049 m < (1 x 7.5 = 7.5 m)

The effective width of the slab can be calculated from;

S = η(1.15)^{n_x – 1}(EI_s/mf₀²)^1/4

η = 0.71 for f₀ > 6.0
n_x = 2.0

S = 0.75(1.15)^{2 – 1} x (210 x 10⁹ x 36.0863 x 10^-6/554.54 x 9.292²)^1/4 = 3.05 m < (2 x 6 = 12)

Modal mass M = mL_effS = 554.54 x 7.04 x 3.05 = 11907 kg

Calculation of Floor Response

As f₀ < 10 Hz, the response is to be assessed according to the low frequency floor recommendations.

a_w,rms = μ_eμ_r (0.1Q/2√2Mζ) x Wρ

Q = 746 N based on an average weight of 76 kg
Take critical damping ratio ζ as 4.68%
Since f₀ > 8Hz, take the weighting factor W = 8/f₀ = 8/9.292 = 0.860
Conservatively assume that μ_e = μ_r = 1.0

Assuming a walking frequency f_p of 2Hz in a maximum corridor length L_p of 15 m;
v = 1.67f_p² – 4.83f_p + 4.5 = 1.52 m/s

ρ = 1 – e^{(-2πζL_pf_p/v)} = 1.0

a_w,rms = 1.0 x 1.0 x [(0.1 x 746)/(2√2 x 11907 x 0.0468)] x 0.86 x 1.0 = 0.0407 m/s²

Response Factor

R = a_w,rms/0.005 = 0.0407/0.005 = 8.14

For an office building, the floor is is acceptable for vibration since the response factor is greater than 8.0.

Structville Announces Webinar on Design of Water Retaining Structures

By

Ubani Obinna

-

July 20, 2020

In our core commitment to provide a flexible platform for learning, improvement, and disseminating civil engineering knowledge, we are delighted to announce that we will be holding our second webinar for the month of July, 2020. Details are as follows;

Theme: Structural Design of Water Retaining Structures
Date: Saturday, 25th July, 2020
Time: 7:00 pm (WAT)
Platform: Zoom
Fee: NGN 2,100 only ($8.00 USD)

Features:

Introduction to design of water retaining structures
Geotechnical aspects of the design of underground water retaining structures (emphasis on water tanks and swimming pools)
Equilibrium and uplift design of underground structures
Analysis of water retaining structures using the classical methods and Staad Pro (finite element modelling)
Structural design of water retaining structures
Serviceability considerations in water retaining structures
Materials and construction methodology of water retaining structures
Interactive question and answer sessions
Detailing of water retaining structures

Get the textbook below FOR FREE by participating the webinar.

To book a space for this webinar, click HERE.

For more information, contact:
WhatsApp: +2347053638996
E-mail: info@structville.com

Functions and Types of Bearings for Contemporary Bridges

By

Ivy Ugorji

-

July 19, 2020

Table of Contents

Bearings are ancillary bridge components that facilitate the transfer of traffic actions, permanent actions, and other environmental actions from the bridge deck down to the substructure, and ultimately, to the ground. To fulfill this function effectively, bearings must be able to accommodate all anticipated service movements (rotations and translations), while also restraining extraordinary movements induced by extreme load cases. The movements allowed by an adjacent expansion joint must be compatible with the displacement restrictions imposed by a bearing. Therefore, bearings and expansion joints must be designed interdependently and in conjunction with the anticipated behavior of the overall structure.

Types of bridge bearing

The type of bearing to be used in a bridge can be determined by a lot of factors. Some prominent issues that can be considered are the strength and the stiffness of the bearing, cost, ease of installation, maintenance cost, etc. The common types of bearings used in contemporary bridges are;

Reinforced elastomeric bearings
fabric pad sliding bearings
steel pin bearings
rocker bearings,
roller bearings
steel pin bearings
pot bearings
disc bearings
spherical bearings, and
seismic isolation bearings.

Reinforced Elastomeric Bearings

A steel-reinforced elastomeric bearing consists of discrete steel shims vulcanized between adjacent discrete layers of elastomer. This vulcanization process occurs under conditions of high temperature and pressure. The constituent elastomer is either natural rubber or synthetic rubber (neoprene). Reinforced elastomeric bearings are broadly classified into four types:

plain elastomeric pads
fiberglass reinforced elastomeric pads
steel reinforced elastomeric pads, and
cotton duck reinforced elastomeric pads.

structure steel laminated bearing — Steel reinforced elastomeric pads

Of these four types, steel reinforced elastomeric pads are used most extensively for bridge construction applications. They are commonly used with prestressed concrete girder bridges and maybe used with other bridge types.

Fabric Pad Bearings

Cotton duck or fabric pads are preformed elastomeric pads reinforced with very closely spaced layers of cotton or polyester fabric. The close spacing of the reinforcing fibers, while allowing fabric pads to support large compressive loads, imposes stringent limits upon their shear displacement and rotational capacities. Unlike a steel reinforced elastomeric bearing having substantial shear flexibility, the fabric pad alone cannot accommodate translational movement. Fabric pads can accommodate very small amounts of rotational movement; substantially less than can be accommodated by more flexible steel reinforced elastomeric bearings.

Pin Bearings

Steel pin bearings are generally used to support high loads with moderate to high levels of rotation about a single predetermined axis. This situation generally occurs with long straight steel plate girder superstructures. Rotational capacity is afforded by rotation of a smoothly machined steel pin against upper and lower smoothly machined steel bearing blocks. Steel keeper rings are typically designed and detailed to provide uplift resistance.

Rocker/Roller Bearings

Steel rocker bearings have been used extensively in the past to allow both rotation and longitudinal movement while supporting moderately high loads. Because of their seismic vulnerability and the more extensive use of steel reinforced elastomeric bearings, rocker bearings are now rarely specified for new bridges.

Rocker Type Bearing — Rocker type of bearing for bridge deck

Steel roller bearings have also been used extensively in the past. Roller bearings permit both rotational and longitudinal movement. Pintles are often used to effect transverse force transfer by connecting the roller bearing to the superstructure above and to the bearing plate below.

Pot Bearings

A pot bearing is composed of a plain elastomeric disc that is confined in a vertically oriented steel cylinder, or pot.

Vertical loads are transmitted through a steel piston that sits atop the elastomeric disc within the pot. The pot walls confine the elastomeric disc, enabling it to sustain much higher compressive loads than could be sustained by more conventional unconfined elastomeric material. Rotational demands are accommodated by the ability of the elastomeric disc to deform under compressive load and induced rotation. The rotational capacity of pot bearings is generally limited by the clearances between elements of the pot, piston, sliding surface, guides, and restraints.

Disc Bearings

A disc bearing relies upon the compressive flexibility of an annular shaped polyether urethane disc to provide moderate levels of rotational movement capacity while supporting high loads. A steel shear resisting pin in the center provides resistance against lateral force. A flat PTFE-stainless steel sliding interface can be incorporated into a disc bearing to additionally provide translational movement capability, either guided or nonguided.

Spherical Bearings

spherical bearing for bridge — Spherical bearing for a bridge

A spherical bearing, sometimes referred to as a curved sliding bearing, relies upon the low-friction characteristics of a curved PTFE-stainless steel sliding interface to provide a high level of rotational flexibility in multiple directions while supporting high loads. Unlike pot bearings and disc bearings, spherical bearing rotational capacities are not limited by strains, dimensions, and clearances of deformable elements. Spherical bearings are capable of sustaining very large rotations provided that adequate clearances are provided to avoid hard contact between steel components.

Spherical bearings are classified into three according to their displacement directions. The three types of spherical bearings are;

Fixed type – Provides only rotation capacity from any direction.
Guided type (Uni-directional sliding) – Provides rotation plus movement in one direction
Free sliding (multi-directional sliding) – Provides rotation plus movement in all directions

Seismic Isolation Bearings

Seismic isolation bearings mitigate the potential for seismic damage by utilizing two related phenomena: dynamic isolation and energy dissipation. Dynamic isolation allows the superstructure to essentially float, to some degree, while substructure elements below move with the ground during an earthquake. The ability of some bearing materials and elements to deform in certain predictable ways allows them to dissipate seismic energy that might otherwise damage critical structural elements.

Source:
Chen W. and Duan L. (2014): Bridge Engineering Handbook – Substructure Design (2nd Edition). CRC Press Taylor and Francis Group. International Standard Book Number-13: 978-1-4398-5230-9

Design of Composite Slab with Profile Metal Deck

By

Ubani Obinna

-

July 15, 2020

Table of Contents

Composite slab with profiled metal decking provides economical solutions for floors of steel framed building systems. This is because they are easier to install, lighter in weight, and faster to execute when compared with precast, prestressed, and solid slab system for steel-framed buildings. The composite action of this floor system is achieved by welding steel studs to the top flange of the steel beams and embedding the studs in the concrete during concrete pouring.

Composite construction reduces frame loadings and results in a cheaper foundation system. Cold-formed thin-walled profiled steel decking sheets with embossments on top flanges and webs are widely used as the profiles. The use of this profiled metal decking eliminates the need for mat reinforcement in the slab and acts as the permanent shuttering for the concrete. Props are therefore not usually required during the process of concreting. This support scheme is usually suitable for spans that are less than 4m (spacing of the supporting beams). The supporting beams themselves can, however, span up to 12m.

Structural engineers usually rely on load/span tables produced by metal deck manufacturers in order to determine the thickness of slab and mesh reinforcement required for a given floor arrangement, fire rating, method of construction, etc. The table below shows an example of a typical load/span table available from one supplier of metal decking.

To download the full SMD technical data sheet for different types of profiled metal decking, click below.

Metal-Profiled-Sheet-Decking_Operations_Technical-Manual Download

Once the composite slab has been designed, the design of the primary and secondary composite beams (i.e. steel beams plus slab) can begin. This is normally carried out in accordance with the recommendations in Part 3: Section 3.1 of BS 5950. In Europe, composite sections are designed according to the requirements of Eurocode 4 (EN 1994 – 1- 1).

The steps in the design of profile metal decking for composite floors are;

Determine the effective breadth of the concrete slab.
Calculate the moment capacity of the section.
Evaluate the shear capacity of the section.
Design the shear connectors.
Assess the longitudinal shear capacity of the section.
Check deflection.

Design Example

The figure below shows a part plan of a composite floor. The slab is to be constructed using profiled metal decking and normal weight, grade 30 concrete. The longitudinal beams are of grade S275 steel with a span of 7.5 m and spaced 3 m apart. Design the composite slab and verify the suitability of 406 x 178 x 67 UKB as the internal beams. The required fire-resistance is 1 hour.

Imposed load = 4 kN/m²
Partition load = 1 kN/m²
Weight of finishes = 1.2 kN/m²
Weight of ceiling and services = 1 kN/m²
Total applied load = 7.2 kN/m² (to be used for slab design i.e. selection from manufacturer’s span-load table)

SLAB DESIGN
From the span-load table above, the configuration below will be satisfactory for the unpropped slab.

Beam span = 7.5 m
Beam spacing = 3.0 m
Total depth of slab h_s = 130 mm
Depth of profile h_p = 60 mm
Overall height of profile h_d= 72 mm
Depth of concrete above profile = 58 mm
Profile: SMD TR60⁺ (1.2 mm gauge)
Gauge = 1.2 mm
Mesh: A142

Typical SMD TR60+ profile

From the manufacturer’s technical data sheet;
Volume of concrete = 0.096 m³/m²
Weight of concrete (wet) = 2.26 kN/m²
Weight of concrete (dry) = 2.21 kN/m²
Weight of profile = 0.131 kN/m²
Height to neutral axis = 33 mm

Shear connector
Connector diameter d = 19 mm
Overall welded height of h_sc = 95 mm
Ultimate tensile strength f_u= 450 N/mm²

Concrete
Normal weight C25/30 concrete
Cylinder trength f_ck= 25 N/mm²
Cube strength f_ck,cube = 30 N/mm²
Secant modulus of elasticity E_cm = 31 kN/mm²

Actions at Construction Stage

Permanent Actions
Self weight of sheeting = 0.131 kN/m² x 3 m = 0.393 kN/m
Allowance for beam self-weight = 1.0 kN/m
Allowance for mesh = 0.05 kN/m² x 3m = 0.15 kN/m
Total g_k = 0.393 + 1 + 0.15 = 1.543 kN/m

Variable Actions
Self-weight of fresh concrete = 2.26 kN/m²x 3m = 6.78 kN/m (note that fresh concrete is treated as variable action in the construction stage)
Construction load = 0.75 kN/m² x 3m = 2.25 kN/m
Total q_k = 6.78 + 2.25 = 9.03 kN/m

At ultimate limit state = 1.35g_k + 1.5q_k = 1.35(1.543) + 1.5(9.03) = 15.63 kN/m

Design moment M_Ed = ql²/8 = (15.63 x 7.5²)/8 = 109.898 kNm
Design shear force V_Ed = ql/2 = (15.63 x 7.5)/2 = 58.61 kN

Actions at the composite stage

Permanent Actions
Self weight of sheeting = 0.131 kN/m² x 3 m = 0.393 kN/m
Allowance for beam self-weight = 1.0 kN/m
Allowance for mesh = 0.05 kN/m² x 3m = 0.15 kN/m
Self-weight of dry concrete = 2.21 kN/m²x 3m = 6.63 kN/m
Weight of finishes = 1.2 kN/m²
Weight of ceiling and services = 1 kN/m²
Total g_k = 0.393 + 1 + 0.15 + 6.63 + 1.2 + 1 = 10.373 kN/m

Variable Actions
Imposed load on floor = 4 kN/m²x 3m = 12 kN/m
Movable partition allowance = 1 kN/m² x 3m = 3 kN/m
Total q_k = 12 + 3 = 15 kN/m

At ultimate limit state = 1.35g_k + 1.5q_k= 1.35(10.373) + 1.5(15) = 36.5 kN/m

Design moment M_Ed = ql²/8 = (36.5 x 7.5²)/8 = 256.6 kNm
Design shear force V_Ed = ql/2 = (36.5 x 7.5)/2 = 136.875 kN

An advanced UK beam S275 is to be used for this design.
F_y = 275 N/mm²
γ_m0= 1.0 (Clause 6.1(1) NA 2.15 BS EN 1993-1- 1:2005)

From steel tables, the properties of 406 x 178 x 67 UKB are;

Depth h = 409.4 mm
Width b = 178.8 mm
Web thickness t_w = 8.8mm
Flange thickness t_f = 14.3 mm
Root radius r = 10.2 mm
Depth between fillets d = 360.4 mm
Second moment of area y axis I_y = 24300 cm⁴
Elastic modulus W_el,y = 1190 cm³
Plastic modulus W_pl,y = 1350 cm³
Area of section A = 85.5 cm²
Height of web h_w = h – 2t_f = 380.8 mm
E_s (Modulus of elasticity) = 210000 N/mm²(Clause 3.2.6(1))

Check out also ….
Design of Steel Beams to BS 5950 – 1: 2000
Structural Analysis of Compound Arch-Frame Structure

Classification of section

ε = √(235/F_y) = √(235/275) = 0.92 (Table 5.2 BS EN 1993-1- 1:2005)

Outstand flange
Flange under uniform compression c = (b – t_w – 2r)/2 = [178.8 – 8.8 – 2(10.2)]/2 = 74.8 mm

c/t_f = 74.8/14.3 = 5.23

The limiting value for class 1 is c/t_f ≤ 9ε = 9 × 0.92
5.23 < 8.28
Therefore, outstand flange in compression is class 1

Internal Compression Part (Web under pure bending)
c = d = 360.4 mm
c/t_w = 360.4/8.8 = 40.954

The limiting value for class 1 is c/t_w ≤ 72ε = 72 × 0.92 = 66.24
40.954 < 66.24
Therefore, the web is plastic. Therefore, the entire section is class 1 plastic.

Member Resistance Verification – Construction Stage

Moment Resistance
For the structure under consideration, the maximum bending moment occurs where the shear force is zero. Therefore, the bending moment does not need to be reduced for the presence of shear force (clause 6.2.8(2))

M_Ed/M_c,Rd ≤ 1.0 (clause 6.2.5(1))

M_c,Rd = M_pl,Rd= (M_pl,y× F_y)/γ_m0

M_c,Rd = M_pl,Rd= [(1350 × 275)/1.0] × 10^-3 = 371.25 kNm

At the construction stage;
M_Ed/M_c,Rd = 109.898/371.25 = 0.296 < 1.0 Ok

Shear Resistance (clause 6.6.2)
The basic design requirement is;

V_Ed/V_c,Rd ≤ 1.0

V_c,Rd = V_pl,Rd= A_v(F_y/ √3)/γ_m0(for class 1 sections)
For rolled I-section with shear parallel to the web, the shear area is;

A_v = A – 2bt_f + (t_w + 2r)t_f (for class 1 sections) but not less than ηh_wt_w

A_v = (85.5 × 10² – (2 × 178.8 × 14.3) + [8.8 + 2(10.2)] × 14.3 = 3854 mm²
η = 1.0 (conservative)
ηh_wt_w= (1.0 × 380.8 × 8.8) = 3351.04 mm²
3854 > 3351.04
Therefore, A_v = 3854 mm²

The shear resistance is therefore;
V_c,Rd = V_pl,Rd= [3854 × (275/ √3)/1.0] × 10^-3 = 612 kN

At the construction stage;
V_Ed/V_c,Rd = 58.61/612 = 0.095 < 1.0 Ok

Shear Buckling
Shear buckling of the unstiffnened web will not need to be considered if;

h_w/t_w≤ 72ε/η

h_w/t_w= 380.8/8.8 = 43.27
72ε/η = (72 × 0.92)/1.0 = 66

43.27 < 66 Therefore shear buckling need not be considered.

Design Resistance of Shear Connectors

Shear connector in a solid slab
The design resistance of a single headed shear connector in a solid concrete slab automatically welded in accordance with BS EN 14555 should be determined as the smaller of;

P_Rd = (0.8 x f_u x π x 0.25d²)/γ_v (Clause 6.6.3.1(1) Equ(6.18) or
P_Rd = [0.29 x α x d² x √(f_ck x E_cm)]/γ_v

Where;
α = 1.0 as h_sc/d = 95/19 > 4 (Equation 6.21)

P_Rd = (0.8 x 450 x π x 0.25 x 19²)/1.25 = 81.7 kN
P_Rd = [0.29 x 1.0 x 19² x √(25 x 31 x 10³)]/1.25 = 73.7 kN

Shear connectors in profiled steel sheeting

For profiled sheeting with ribs running transverse to the supporting beams, P_Rd,solid should be multiplied by the following reduction factor;

k_t= (0.7/√n_r) x (b₀/h_p) x (h_sc/h_p – 1)

b₀ = width of a trapezoidal rib at mid height of the profile = (133 + 175)/2 = 154 mm
h_sc = 95 mm
h_p = 60 mm
n_r = 1.0 (for one shear connector per rib)

k_t= (0.7/√1.0) x (154/60) x (95/60 – 1) = 1.0

Therefore P_Rd = k_tP_Rd,solid = 1.0 x 73.7 = 73.7 kN
The design resistance per rib = n_rP_Rd = 1 x 73.7 = 73.7 kN

Degree of shear connection

For composite beams in buildings, the headed shear connectors may be considered as ductile when the minimum degree of shear connection given in clause 6.6.1.2 is achieved.

For headed shear connectors with;
h_sc ≥ 4d and 16mm ≤ d ≤ 25 mm

The degree of shear connection may be determined from;

η = N_c/N_c,f

Where;
N_c is the reduced value of the compressive force in the concrete flange (i.e. force transferred by the shear connectors)
N_c,f is the compressive force in the concrete flange at full shear connection (i.e. the minimum of the axial resistance of the concrete and the axial resistance of the steel)

For steel sections with equal flanges and L_e < 25 m;

η ≥ 1 – (355/f_y) x (0.75 – 0.03L_e) where ≥ 0.4
L_e = distance between points of zero moment = 7.5 m
η ≥ 1 – (355/275) x (0.75 – 0.03 x 7.5) = 0.322, therefore η = 0.4

Degree of shear connection present

To determine the degree of shear connection present in the beam, the axial resistances of the steel and concrete are required (N_pl,a and N_c,frespectively)

stress block for calculating resistances of composite sections — Stress block for calculating the resistances of concrete sections

Determine the effective width of the concrete flange

At the mid-span, the effective width of the concrete falnge is;

b_eff= b₀+ ∑b_ei

Composite section effective width dimensions — Effective flange width of composite section

For n_r = 1.0, b₀ = 0 mm
b_ei = L_e/8 but ot greater than b_i

L_e = 7.5 m (point of zero moment)
b_i= distance from the outside shear connector to a point between adjacent webs. Therefore;

b₁ = b₂ = 1.5 m
b_e1= b_e2 = L_e/8 = 7.5/8 = 0.9375 m

The effective flange width is therefore
b_eff = b₀ + b_e1 + b_e2 = 0 + 0.9375 + 0.9375 = 1.875 m = 1875 mm

Compressive resistance of the concrete flange

The design strength of the concrete f_cd = 25/1.5 = 16.7 N/mm²

The TR60⁺ profile has a 12 mm deep re-entrant above the stiffener making the overall profile depth h_d = 12 mm + 60 mm = 72 mm

The compressive resistance of the concrete flange is therefore;
N_c,f = 0.85f_cdb_effh_c = 0.85 x 16.7 x 1875 x 58 x 10^-3 = 1543.7 kN

Tensile Resistance of the steel member
N_pl,a = f_y.A = 275 x 85.5 x 10² x 10^-3 = 2351.25 kN

The compressive force in the concrete at full shear connection is the lesser. Therefore N_c= 1543.7 kN

Resistance of the shear connectors

n is the number of shear connectors present to the point of maximum bending moment. In this example, there are 7.5(2 x 0.333) = 12 ribs available for positioning shear connectors per half span.

N_c = n x P_Rd = 12 x 73.7 = 884.4 kN

The degree of shear connection present therefore is;

η = N_c/N_c,f = 884.4/1543.7 = 0.572 > 0.40 (Okay)

Design Resistance of the Cross-section at the composite stage

Bending Resistance

According to clause 6.2.1.2, the plastic rigid theory may be used for one connector per trough. With partial shear connection, the axial force in the concrete flange N_cis less than N_pl,a (884.4 kN < 2351.25 kN). Therefore, the plastic neutral axis lies within the steel section. Assuming that the plastic neutral axis lies a distance x_pl below the top of the flange of the section, where;

x_pl = (N_pl,a – N_c)/2f_yb = (2351.25 – 884.4)/(2 x 275 x 178.8) = 0.0149 m = 14.916 mm > t_f (14.3 mm)

Therefore the plastic neutral axis lies below the top flange.

stress block distribution — Stress block of composite cross-section

y_c = N_c/[0.85f_ckb_eff /γ_c] ≤ h_c
y_c = (884.4 x 1000)/[0.85 x 25 x 1875/1.5] = 33.28 mm

M_Rd = N_c(h_c + d_a – y_c/2) + 2bt_ff_y(d_a – t_f/2) + t_w(y_a – t_f)(f_y)(2d_a – y_a – t_f)
M_Rd = (884.4 x 10³) x (130 + 204.7 – 33.28/2) + 2 x 178.8 x 14.3 x 275 x (204.7 – 14.3/2) + 8.8(14.92 – 14.3) x 275 x (2 x 204.7 – 14.92 – 14.3) = 559669744.2 Nmm = 559.669 kNm

M_Ed = 256.6 kNm

M_Ed/M_Rd = 256.6/559.669 = 0.458 < 1.0 (Okay)

Shear Resistance at the Composite Stage

The shear resistance is therefore;
V_c,Rd = V_pl,Rd= [3854 × (275/ √3)/1.0] × 10^-3 = 612 kN
V_Ed = 136.875 kN
V_Ed/V_c,Rd = 136.875/612 = 0.223 < 1.0 Ok

Longitudinal shear resistance of the slab

Crack control mesh as transverse reinforcement

Neglecting the contribution of the steel, we ned to verify that;

A_sff_sd/S_f > v_Edh_f/cotθ

Where;
v_Ed is the design longitudinal shear stress in the concrete slab
f_sd is the design yield strength of the reinforcing mesh = 0.87f_yk = 0.87 x 500 = 434.8 N/mm²
h_f = depth of the concrete above the profiled sheeting = 70 mm
θ angle of failure (try 26.5^o)
A_sf/S_f = A_t (for the plane of failure shown as section a-a)
A_t is the cross-sectional area of transverse reinforcement mm²/m)

The verification equation therefore becomes;

A_tf_yd > v_Edh_f/cotθ

The required area of tensile reinforcement At must satisfy the following;

At > v_Edh_f/f_ydcotθ

The longitudinal shear stress is given by;

v_Ed = ∆F_d/h_f∆x

Where;
∆x is the critical length under consideration, which is usually taken as the distance between the maximum bending moment and the support = L/2 = 7.5/2 = 3.75m
∆F_d = N_c/2 = 884.4/2 = 442.2 kN

v_Ed = ∆F_d/h_f∆x = (442.2 x 10³)/(70 x 3750) = 1.68 N/mm²

v_Edh_f/f_ydcotθ = (1.68 x 70)/(434.8 x cot 26.5^o) = 0.134 mm²/mm

For the arrangement, the area of tensile reinforcement required is 134 mm²/m
Therefore A142 mesh provided is adequate (A_sprov= 142 mm²/m)

Crushing of the concrete flange

It is important to verify that
v_Ed < vf_cdsinθ_fcosθ_f
v = 0.6(1 – f_ck/250) = 0.6 x (1 – 25/250) = 0.54
vf_cdsinθ_fcosθ_f = 0.54 x 16.67 x sin(26.5) x cos(26.5) = 3.59 N/mm²

(v_Ed) 1.68 N/mm² < 3.59 N/mm² (Okay)

Serviceability limit state

Modular ratios
For short term loading, the secant modulus of elasticity should be used. E_cm = 31 kN/mm². This corresponds to a modular ratio of;

n₀ = E_s/E_cm = 210/31 = 6.77 (clause 5.4.2.2)

For long term loading;
n_L = n₀(1 + ψ_Lϕ_t)
Where ψ_L is the creep multiplier taken as 1.1 for permanent loads and ϕ_t is the creep coefficient taken as 3.0.
n_L = 6.77 x (1 + 1.1 x 3) = 29.11

When calculating deflection due to variable action, the modular ratio is taken as;

n = 0.333n_L + 0.667n₀ = 0.333(29.11) + 0.667(6.77) = 14.22

Since the beam is simply supported, use the gross value of second moment of area, I_c, of the uncracked section to calculate deflection.

I_c= I_y + [b_eff(h_s – h_p)³/12∙n_i] + [A∙b_eff(h_s – h_p)(h + h_s + h_p)²]/4[A∙n_i + b_eff(h_s – h_p)]

For n₀ = 6.77
I_c= 24300 x 10⁴ + [1875(130 – 60)³/(12 x 6.77)] + [85.5 x 10² x 1875(130 – 60) x (409.4 + 130 + 60)²]/4[85.5 x 10² x 6.77 + 1875(130 – 60)] = 78385 x 10⁴ mm⁴

For n_L = 29.11
I_c= 24300 x 10⁴ + [1875(130 – 60)³/(12 x 29.11)] + [85.5 x 10² x 1875(130 – 60) x (409.4 + 130 + 60)²]/4[85.5 x 10² x 29.11 + 1875(130 – 60)] = 50999 x 10⁴ mm⁴

For n = 14.22
I_c= 24300 x 10⁴ + [1875(130 – 60)³/(12 x 14.22)] + [85.5 x 10² x 1875(130 – 60) x (409.4 + 130 + 60)²]/4[85.5 x 10² x 14.22 + 1875(130 – 60)] = 64543 x 10⁴ mm⁴

Deflection due to actions on the steel at the construction stage;
Actions = self weight of fresh concrete + mesh + sheeting + steel section
w₁ = 5gl⁴/384EI = (5 × 8.323 × 7500⁴)/(384 × 210000 × 24300 × 10⁴) = 6.719 mm

Deflection due to permanent action on the steel at the composite stage;
Actions = weight of finishes + ceiling and services
w₂ = 5gl⁴/384EI = (5 × 6.6 × 7500⁴)/(384 × 210000 × 50999 x 10⁴) = 2.54 mm

Deflection due to variable action on the steel at the composite stage;
Actions = Imposed load + partition allowance
w₃ = 5ql⁴/384EI = (5 × 15 × 7500⁴)/(384 × 210000 × 64543 x 10⁴) = 4.559 mm

Total deflection = w₁ + w₂ + w₃ = 6.719 + 2.54 + 4.559 = 13.818 mm

Allowable deflection = L/360 = 7500/360 = 20.833 mm.
13.818 < 20.833 Therefore deflection is okay.

Effects of Trees on Wind Comfort of Pedestrians

By

Peace Ikpotokin

-

July 12, 2020

Pedestrian wind comfort can be improved when horizontally incoming airflow passes through trees in the urban areas. This is according to recent research carried out in the Department of Environmental Atmospheric Sciences, Pukyong National University, Busan, Republic of Korea, and published in Elsevier – Sustainable Cities and Societies. In the study, the authors applied computational fluid dynamics incorporating tree drag parameters to evaluate how trees improved the wind comfort of pedestrians.

The way wind is perceived at the ground level depends on a lot of factors such as wind direction, wind speed, obstacles, and many other parameters. This experience affects pedestrians’ comfort and safety, and can impact the financial returns or economic viability of an area. According to Lawson-based wind comfort criterion, wind speed exceeding 10 m/s can be uncomfortable for pedestrians at the ground level, while wind speed above 15 m/s is outrightly dangerous. Other wind comfort criteria exist such as that proposed by Davenport.

Trees are known to function as porous obstacles to airflow, and they eventually affect wind speed and direction. The presence of high rise buildings and urban densification has been observed to reduce airflow in city centers and may lead to increased urban heat and poor dispersal of pollutants. However, the effect of wind on tall buildings can amplify wind pressure in the surroundings due to issues like vortex shedding, reverse flow, channeling effects, etc. This can lead to discomforting wind effects on pedestrians. Therefore, by applying computational fluid dynamics model (CFD) with tree drag parameterization scheme, the researchers were able to evaluate the effect of trees on pedestrian wind comfort in Pukyong National University campus. The CFD model used in the study was verified with field observations.

The CFD model used in the study was based on Reynolds-averaged Navier–Stokes (RANS) equations and assumes a three-dimensional, non-rotating, non-hydrostatic, incompressible airflow system. Turbulence was parameterized using the renormalization group (RNG) k-ε turbulence closure scheme. Tree drag terms were introduced into the momentum, turbulent kinetic energy (TKE), and TKE dissipation rates equations to account for the loss of airflow pressure due to winds.

The target area for the research was the Pukyong National University (PKNU) campus (See Fig. 1a) which is located in the downtown area and is surrounded by commercial and residential areas. PKNU boasts relatively high vegetation density for student recreational spaces and ecologically friendly landscaping within the campus. Regions A and B (Fig. 1b) contains a dense forest of trees taller than 10–15 m. Several tree species are planted along the PKNU boundary (region C in Fig. 1b).

The authors adopted the wind comfort criteria proposed by Isyumov and Davenport (1975), which distinguish four sensory levels (good, tolerable, unpleasant, and dangerous) for four categories of human activity or activity location (Table 1). These sensory levels are determined by the Beaufort wind force scale (BWS), represented by wind speeds at 10 m above the ground level. To evaluate wind comfort at the pedestrian level (z =1.75 m), they used the BWS values converted into pedestrian height.

Table 1: Sensory levels in terms of suitability for outdoor activities, represented by the Beaufort wind force scale (BWS) (Isyumov & Davenport, 1975).

From the study, poor wind comfort for outdoor activities (BWSs ≥ 4) was observed in the areas without trees, mainly around the edges of buildings, in the windward regions of buildings, in the spaces between buildings, and in wide, unobstructed areas. This was attributed to venturi effects between the spaces in buildings. In the case of where trees were present, the BWS values declined by one to three levels, improving the overall level of wind comfort within the PKNU campus.

The highest ABWS and TBWS values (≥ 4) were observed near the southeast perimeter of the PKNU campus, where a 10-lane road is located. By contrast, the lowest ABWS and TBWS values (≤ 3) were observed in the southwest and northwest of the campus. Where trees were present, the overall wind speeds inside the campus were reduced due to drag.

The authors concluded that tree arrangement can reduce wind speeds in the lee of the trees by more than half and proposed that trees should be planted at 90° to the dominant wind direction. The presence of trees decrease wind speeds. However, because wind speeds can increase in surrounding areas without trees, the effects of trees on strong winds in such areas should be assessed.

Reference
Kang G., Kim J., Choi W. (2020): Computational fluid dynamics simulation of tree effects on pedestrian wind comfort in an urban area. Sustainable Cities and Societies 56 (2020)102086. https://doi.org/10.1016/j.scs.2020.102086

Disclaimer:
Contents of this research article have been shown on www.structville.com because it is an open access article under creative commons licence (http://creativecommons.org/licenses/BY/4.0). All other rights belong to the authors and Elsevier.

Difference Between Pile Load Test and Pile Integrity Test

By

Ubani Obinna

-

July 10, 2020

Pile foundations are slender structures used to transmit superstructure load to firmer sub-soil stratum beneath the natural ground surface. They can also be used for other purposes such as resisting heavy lateral forces, compaction of soils (compaction piles), avoiding excessive settlement, etc. Due to their importance in civil engineering structures, piles are usually subjected to tests such as pile load tests and pile integrity tests before they are loaded. These two tests are completely different and are sometimes confused for one another, even though they do not serve the same purpose. This article aims to highlight the difference between these two tests.

Pile Load Test

Generically, pile load test can be described as a reliable method of pile foundation design which involves loading constructed piles on-site to determine their load-carrying capacity. A pile load test involves applying increments of static loads to a test pile and measuring the settlement. The load is usually jacked onto the pile using either a large deadweight or a beam connected to two uplift anchor piles to supply reaction for the jack. Generally, an installed pile, weights, deflection gauge, hydraulic jack, and load indicator are required for a pile load test.

Loading of test piles is usually applied in increments of 25% of the total test load which should be 200% of the proposed design load. After the load test, the load-settlement curve is plotted and the failure load determined. Eurocode 7 permits three different methods for the design of pile foundations which are;

By testing (static load test, ground testing result, dynamic ground testing)
By calculation (empirical or analytical)
By observation

It is important that the validity of static load test be checked using calculations.

Pile Integrity Test

Pile integrity test (PIT) is a non-destructive method of testing of piles that is used for qualitative evaluation of the physical dimensions, continuity, and consistency of materials in a bored (cast in-situ) pile. This test is very important for quality control and quality assurance of piles at great depth.

The three most common methods of carrying out pile integrity tests are;

Low-strain pile integrity test
Crosshole sonic logging
Thermal integrity test

In the low-strain impact integrity testing, the head of the pile shaft is subjected to impact using a tool like a simple hammer and the response is determined using a high precision transducer. The transducer can either be an accelerator, or a velocity sensor. Low-strain pile integrity tests can provide information such as embedment length, changes in cross-section (such as bulging), discontinuity (such as voids), and consistency of pile materials (such as soil inclusion and segregation). However, it cannot provide information such as bearing capacity and cannot be applied to pile caps.

Differences and similarities between pile load test and pile integrity test at a glance

Pile Load Test	Pile Integrity Test
Used for determining bearing capacity of piles	Used for determining physical properties of constructed piles
Can evaluate pile settlement under load	Cannot evaluate pile settlement
Expensive to set up	Cost effective
Takes time to complete	Very quick test
Cannot provide the embedment length of the pile	Provides embedment length of the pile
Cannot give information on the quality of the piling job	Provides information on the quality of the piling job

Therefore, pile load test and pile integrity tests should be carried out as soon as piling jobs are concluded on site before the next stage of the construction commences.

Design of Pile Cap Using Staad Foundation Advanced

By

Peace Ikpotokin

-

July 9, 2020

Pile caps are rigid plate structures that are used to transfer superstructure load from columns to a group of piles. They are usually subjected to bending and shear forces, and shear considerations usually govern the thickness design of pile caps. The three main approaches that are used in the analysis of pile caps are;

Truss Analogy
Bending analogy, and
Finite element analysis

While truss analogy and bending theory can be easily carried using quick manual calculations, finite element analysis usually require the use of computer models. In this article, we are going to explore the potentials of Staad Foundation Advanced Software in the analysis and design of pile caps.

A quick design of pile caps can be done on Staad Foundation Advanced using the Foundation Toolkit option. This approach does not require importing models and can be used for quick stand-alone design when the column load and geotechnical parameters of the soil are available. To use this option, launch the ‘Staad Foundation Advanced‘, click on ‘New Project‘, and select ‘Foundation Toolkit‘ labelled as shown below.

Step 1: Launch the foundation toolkit

Step 2: Create Pile Cap Job

When the Foundation Toolkit opens, go to ‘Main Navigator‘, and from ‘Project Info‘ drawdown list, select ‘Create Pile Cap Job‘ as shown below.

Step 3: Select design code, units, and pile layout

When the ‘Pile Cap Job’ is launched, select the desired code of practice, unit, and click ‘Next’. The pile layout can be left as predefined.

Step 4: Define the load

On clicking ‘Next’, the dialog box for load comes up. Make sure that the unit is consistent as desired, and for this exercise, I am applying a factored column load of 3500 kN. If there are other forces such as moment and shear coming from the column, you can define them also.

Step 5: Define Load Combination

Since we are dealing with an already factored load, select ‘User Defined‘ from the drawdown list of load combination. If you have defined dead load, live load, wind load etc in Step 4, you can select the desired code of practice for the combination of the loads. Since I defined my factored load as dead load, I assigned a factor of 1.0 to dead load at ULS and SLS (actually I am not interested in SLS in this design). Then click ‘Next‘

Step 6: Define the design parameters

In this case, the column dimensions are taken as 450 mm x 450 mm, and the thickness of the pile cap was taken as 1300 mm. Other design parameters specified are as shown below.

Step 7: Select pile arrangement

The diameter of the pile was selected as 750 mm, with a spacing of 2250 mm. The safe working load of the pile was taken as 900 kN. You can also input the uplift and lateral load capacity of the pile. The edge distance is taken as (diameter of pile/2 + 150 mm) – where 150 mm is the overhang from the edge of the pile to the edge of the pile cap. Then click on ‘Calculate‘.

This brings the possible pile arrangements based on the safe working load and the superstructure load. For this tutorial, the arrangement below was adopted. The simple idea behind it is simply (Column load/pile safe working load). Note that for practical purposes, serviceability limit state load should be used when selecting the number of piles. Then click ‘Ok‘ and ‘Next‘.

Step 8: Finish the model

Step 9: Carry out the Design

Clicking ‘Finish‘ returns you to the ‘Main Navigator‘ page, where you can click on ‘Design‘ to carry out the design of the pile cap.

Step 10: View the output

The output page is where you can view the geometry drawing, details and schedule drawing, calculation sheet, and graphs.

The design approved the 1300 mm thick pile cap provided, and provided Y16@100 mm c/c reinforcement. You can go ahead and print the calculation sheet which you can download below.

FOUR-PILE-CAPS-STRUCTVILLE Download

Thank you for visiting Structville Today, and God Bless You

QUIZ START

Modeling of Soils Using Isogeometric Analysis

By

Ivy Ugorji

-

July 8, 2020

Researchers from the Department of Construction Sciences, Lund University, Sweden have presented isogeometric analysis as an alternative to finite element analysis for modelling of soil plasticity. In a study published in the year 2017 in Geomaterials Journal, the researchers were able to show that isogeometric analysis showed good agreement with finite element method for drained soils in two- and three-dimensions. The research, therefore, suggested that isogeometric analysis is a good alternative to conventional finite element analysis for simulations of soil behavior.

Isogeometric analysis is a numerical method that uses non-uniform rational B-splines (NURBS) as basis functions instead of the Lagrangian polynomials often used in the finite element method. These functions have a higher-order of continuity and therefore makes it possible to represent complex geometries exactly. The basic idea behind isogeometric analysis is to use splines (NURBS) as basis functions for computational analysis by applying them directly. This allows the same basis function to be used for discretzation and for analysis.

A1 1 — Representation of quadratic B-spline basis function with knot vector Ξ = {0, 0, 0, 1, 2, 3, 4, 5, 5, 5} *(Spetz et al, 2017)*

A2 2 — Representation of quadratic Lagrangian basis function (Spetz et al, 2017)

Since being introduced by Thomas J.R. Hughes at the University of Austin, Texas in the year 2005, isogeometric analysis has found numerous applications in engineering such as analysis of thin plates and shells, soil-structure interaction, fluid-structure interaction, flow through porous media, etc. However, finite element analysis has been used extensively for constitutive modelling of soils for the design of foundations, retaining walls, slope stability problems etc.

For the purpose of the research, Drucker-Prager criterion and the theory of plasticity was used by the researchers to evaluate the influence of the NURBS-basis functions on the plastic strains for granular materials against the conventional finite element analysis approach.

To compare the results of the findings, a 2D model of a strip footing on sandy silt was analyzed. The problem was solved for plane strain conditions using quadratic NURBS based IGA and conventional FEA with 5 different meshes. In order to compare the two methods, the element meshes were constructed using quadratic isoparametric elements for both IGA and conventional FEA.

k11 — Load/displacement response at point A and B for the finest mesh (4800 elements) *(Spetz et al, 2017)*

The first point, A, denotes the center of the footing and the second point, B denotes the edge of the footing. It was observed that the displacements in the model are in good agreement at center of the footing but a minor difference was observed between the displacements from the isogeometric and conventional finite element analysis at the edge of the footing.

References
Spetz, A. , Tudisco, E. , Denzer, R. and Dahlblom, O. (2017): Isogeometric Analysis of Soil Plasticity. Geomaterials, 7, 96-116. doi: 10.4236/gm.2017.73008.

Featured Image: Institute for Structural Mechanics, University of Stuttgart. https://www.ibb.uni-stuttgart.de/en/research/shells-fem-iga/

Disclaimer:
This research article has been featured on www.structville.com because it is an open access article that permits unrestricted use and distribution provided the original source of the article has been cited. See the Creative Commons Attribution International License (CC BY 4.0). http://creativecommons.org/licenses/by/4.0/

Short span composite beam and composite slab with metal decking

Slimdek

Cellular composite beams with composite slabs and steel decking

Slimflor® beams with precast concrete units

Long-span composite beams and composite slabs with metal decking

Composite beams with precast units

Non-composite beams with precast units

Criteria for considering second order effects

Methods for determining second order effects

Types of bridge bearing

Reinforced Elastomeric Bearings

Fabric Pad Bearings

Pin Bearings

Rocker/Roller Bearings

Pot Bearings

Disc Bearings

Spherical Bearings

Seismic Isolation Bearings

Design Example

Actions at Construction Stage

Actions at the composite stage

Classification of section

Member Resistance Verification – Construction Stage

Design Resistance of Shear Connectors

Design Resistance of the Cross-section at the composite stage

Serviceability limit state

Pile Load Test

Pile Integrity Test

Differences and similarities between pile load test and pile integrity test at a glance

EDITOR PICKS

POPULAR POSTS

POPULAR CATEGORY

ABOUT US

FOLLOW US

Slimflor^® beams with precast concrete units