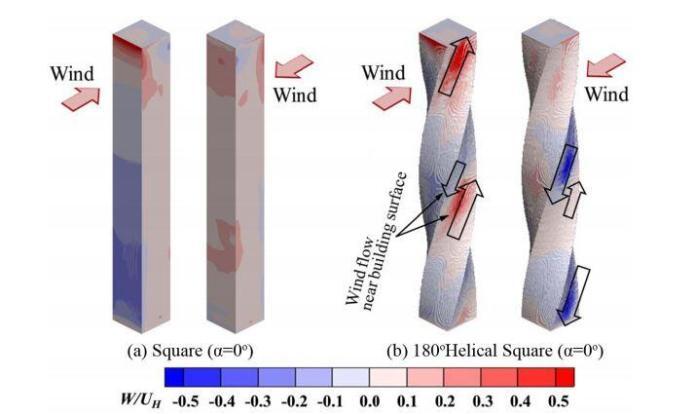
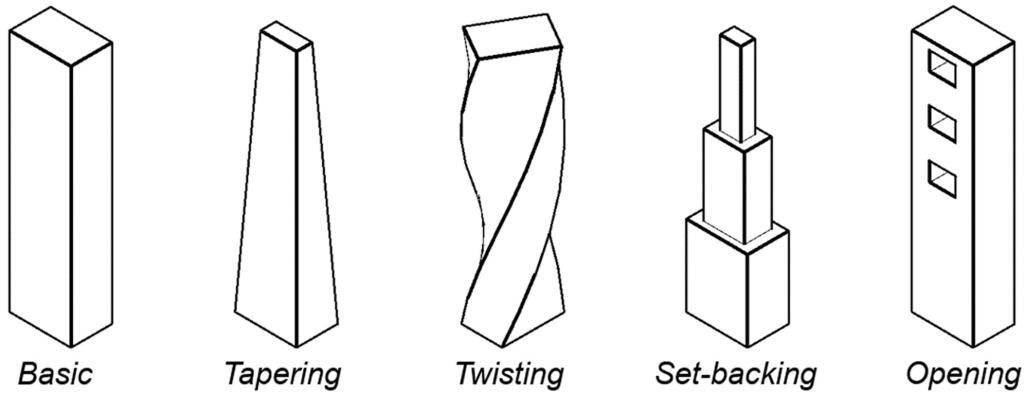
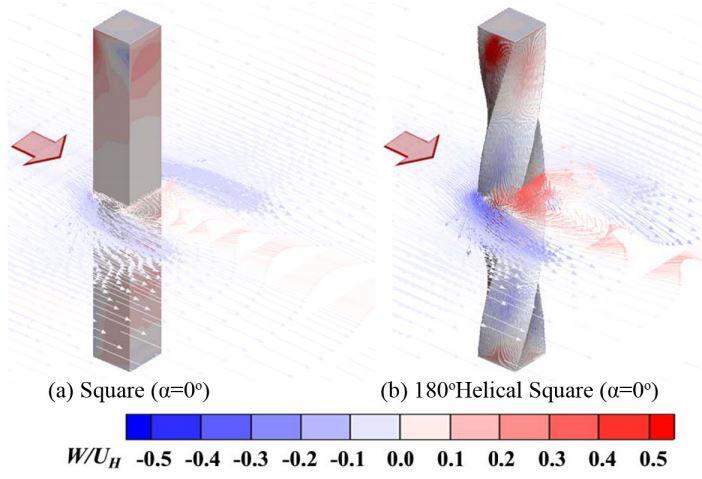
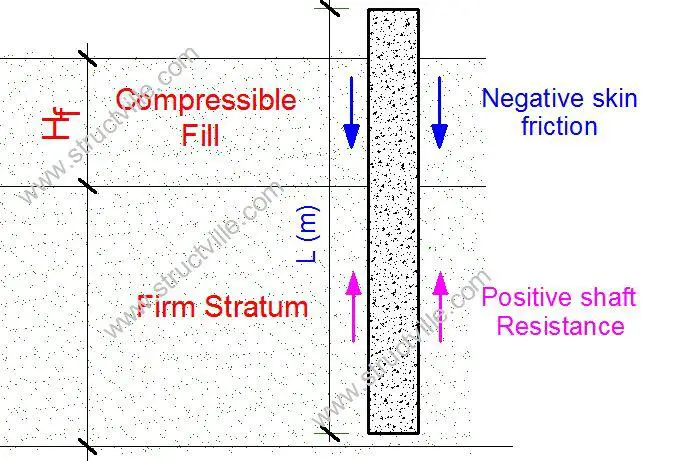
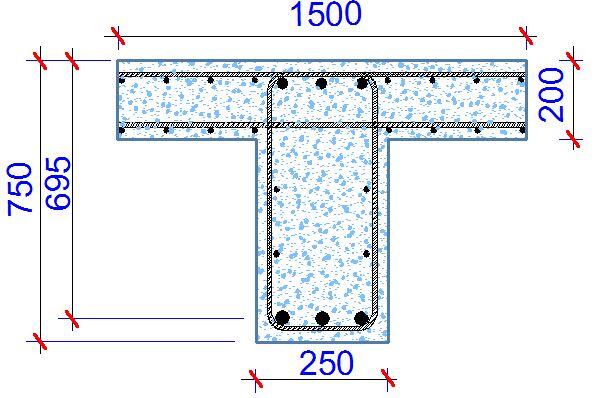
Concrete is arguably the most widely used construction material in the world. It is produced from a mixture of cement, sand, gravel, and water through a process known as hydration reaction. In its fresh state, concrete can be poured into different moulds and forms to achieve the desired shape. This is one of the reasons why it is an attractive construction material.
In its hardened state, concrete is very good in compression, but weak in tension. In order to augment this inherent weakness of concrete in tension, steel reinforcement is usually introduced to take up the tensile stresses. Any structure made up of steel reinforcement embedded in concrete to form a load resisting composite is known as a reinforced concrete structure. The process of specifying the member sizes of concrete and the area of steel required to ensure good performance of a structure under load is known as reinforced concrete design.
The key to the good performance of reinforced concrete structures lies in the complementary action of concrete and steel. This composite but complementary action is highlighted in the Table below;
| Property | Concrete | Steel |
| Tensile strength | Poor | Good |
| Compressive strength | Good | Good (but slender members will buckle) |
| Shear strength | Fair | Good |
| Durability | Good | Fair (will corrode if unprotected) |
| Fire resistance | Good | Poor (will lose strength at elevated temperature) |
By looking at the table above, you can see that all the desirable properties listed will be achieved if the two materials are combined. The structural design of reinforced concrete structures aims at taking advantage of the different but complementary characteristics of concrete and steel. Some of the basic theoretical assumptions that are made in design are as follows;
- Concrete’s resistance to tension is zero (not practically true, the tensile strength of concrete is about 10% of its compressive strength, but this strength is usually ignored in ultimate limit state design)
- The bond between steel and concrete is perfect
Based on these assumptions, all tensile stresses in a structure are transferred to the reinforcements during design. These tensile stresses are transferred by the bond between the concrete and the reinforcement. Perfect bond assumption demands that the strain in the reinforcement is identical to the strain in the adjacent concrete (compatibility of strains). Furthermore, the coefficients of thermal expansion for steel and for concrete are of the order of 10 x 10-6 per ℃ and 7-12 x 10-6 per ℃ respectively. These values are sufficiently close that problems with bond seldom arise from differential expansion between the two materials over normal temperature ranges.
Practically, if the bond between reinforcement and steel is not adequate. the reinforcing bars will slip within the concrete and there will be no composite action. Adequate bonding is ensured by detailing the structure such that the reinforcement is properly anchored in the concrete. Reinforcement bars are also ribbed in order to facilitate bonding with concrete.

It is normal for cracking to occur in concrete when it subjected to tensile or flexural stress. This cracking, however, does not mean that the structure is not safe provided it is adequately reinforced that the crack width is kept to a minimum. If the crack width is excessive, there may be serviceability and/or durability issues (corrosion of reinforcement) in the structure.
Furthermore, when the compressive or shearing forces exceed the strength of the concrete, then steel reinforcement must again be provided to supplement the load-carrying capacity of the concrete. For example, compression reinforcement is generally required in a column, where it takes the form of vertical bars spaced near the perimeter. To prevent these bars buckling, steel binders are used to assist the restraint provided by the surrounding concrete.
Reinforced concrete has a lot of applications in construction, and has been applied in a lot of structures worldwide – bridges, industries, residential buildings, highrise buildings, swimming pools, retaining walls, highways (rigid pavement) etc. The design of any reinforced concrete structure should start with the understanding and behaviour of the structure to be designed under load. The designer will need to specify the load path (how the load will be transferred from the superstructure to the foundation).
For instance, to design a building, the structure can be broken down into the following elements. This is what is called the general arrangement of the building.
- Beams: horizontal members carrying lateral loads
- Slab: horizontal plate elements carrying lateral load
- Columns: vertical members carrying primarily axial load but generally subjected to axial load and moment
- Walls: vertical plate elements resisting vertical, lateral or in-plane loads
- Bases and foundations: pads or strips supported directly on the ground that spread the loads from columns or walls so that they can be supported by the ground without excessive settlement. Alternatively, the bases may be supported on piles.
Knowledge of reinforced concrete design starts from knowing how to design the separate elements listed above. However, it is important to recognize the function of the element in the complete structure and that the complete structure or part of it needs to be analysed in order to obtain actions for design.
Designers are expected to follow a generally accepted code of practice in their design and detailing. This is to enable a quick check and understanding of the design by other engineers. Some codes of practice used in the design of concrete structures across the world are;
EN 1992-1-1:2004 – Eurocode 2: Design of concrete structures – Part 1-1: General rules and rules for buildings (European Union)
BS 8110-1:1997 – Design of reinforced concrete structures – Rules and general rules for buildings
ACI 318-19: Building Code Requirements for Structural Concrete and Commentary
IS 456-2000: Plain and Reinforced Concrete – Code of Practice (Indian Standards)
CSA A23.3:2014 – Design of concrete structures (Canadian Standards Association)
AS 3600:2018 – Concrete structures (Standards Australia)