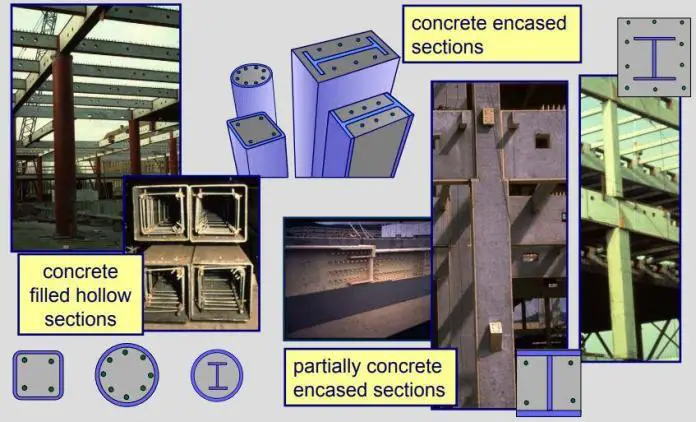
A multi-storey building can develop lateral vibrations in the two principal directions and torsional vibration around its vertical shear centre axis. The natural frequency of a structure is the frequency at its free or natural vibration. For a simple mass-spring system, the natural frequency is given by Equation (1);
f = 1/2π √(k/m) —– (1)
Where f is the natural frequency (Hz), and k and m are the stiffness and mass respectively.
Low-rise buildings have high natural frequencies, while tall flexible buildings are characterized by their low natural frequencies. Resonance occurs when the frequency of excitation is close to a system’s natural frequency. Therefore low-rise buildings are more susceptible to earthquake-induced load than to wind loads.
Although tall buildings are flexible and are therefore further away from the peak in the spectral density function of earthquakes, they are susceptible to the low-frequency range of seismic action. Wind poses a special hazard to tall buildings since their fundamental frequencies move towards the wind-spectrum peaks with higher flexibility. Therefore, it is important to calculate the natural frequency of multi-storey buildings.
Zalka (2013) suggested manual procedures for calculating the natural frequency of multi-storey frames. The equations used for calculating the natural frequency of a multi-storey frame is based on the whole bracing system, which can be characterised by the shear stiffness of the frameworks and coupled shear walls, the global bending stiffness of the frameworks and coupled shear walls, and the local bending stiffness of the individual columns/wall sections, shear walls, and cores.
By combining the individual bracing elements, linked by the floor slabs, to form a single cantilever, an equivalent system can be established with shear stiffness K, global bending stiffness EIg and local bending stiffness EI. The shear stiffness and the global bending stiffness are not independent of each other and can be incorporated into an effective shear stiffness, leading to a single equivalent column with effective shear stiffness Ke and bending stiffness EI.
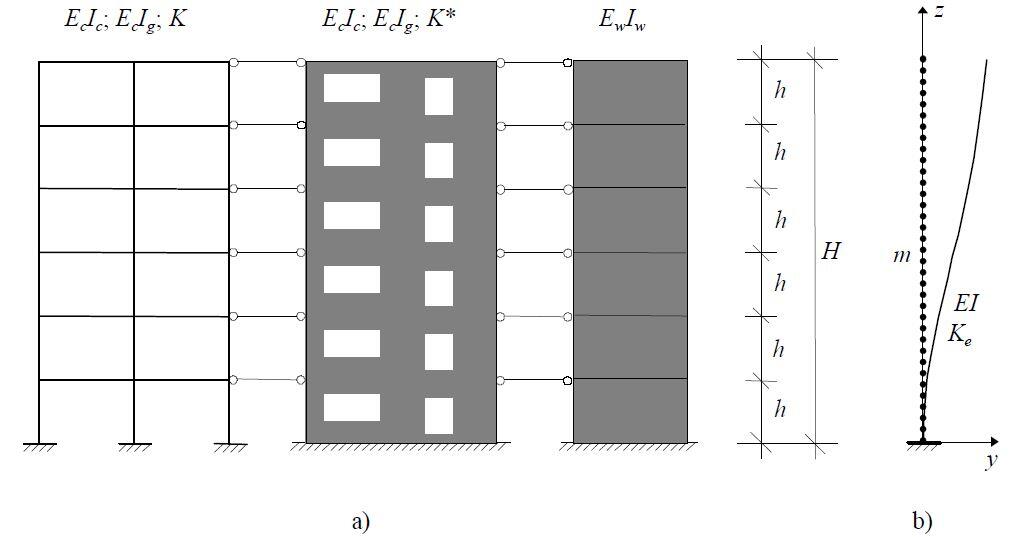
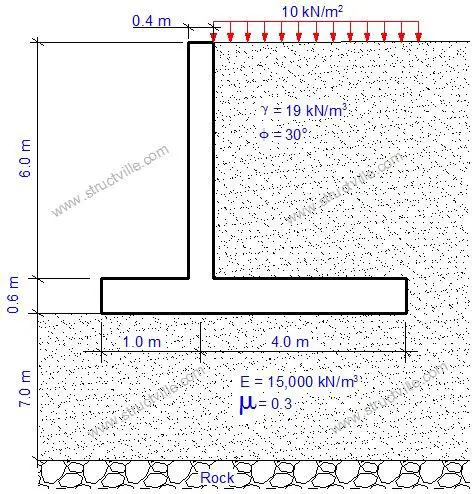
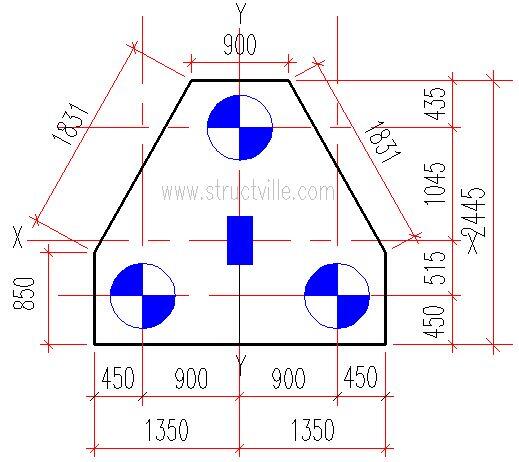
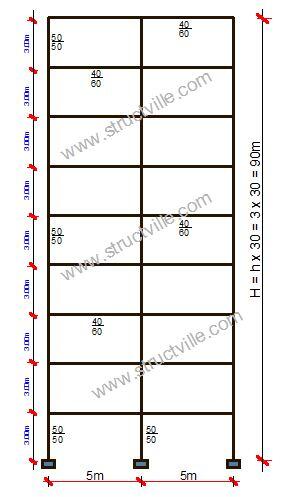
We will show how this is done with a solved example. Let us consider the frame of a tall building shown in Figure 2. The properties of the building are as follows;
Total height of building H = 90 m
Number of storeys n = 30
Height of each storey h = 3 m
Width of each bay L = 5 m
Dimension of columns = 500 x 500 mm
Dimension of beams = 600 x 400 mm
Modulus of elasticity of concrete = 28 × 106 = kN/m2
Mass at each level = 2100 kg/m
Solution
Second moment of area of beams IB = (bd3)/12 = (0.4 × 0.63)/12 = 0.0072 m4
Second moment of area of columns IC = (bd3)/12 = (0.5 × 0.53)/12 = 0.0052083 m4
Flexural rigidity of beams EIb = 28 × 106 × 0.0072 = 201600 kN.m2
Flexural rigidity of columns EIC = 28 × 106 × 0.0052083 = 145833.33 kN.m2
The part of shear stiffness associated with beams = KB = ∑(12EIb)/(Lih) = 2 × [(12 × 201600)/(5 × 3)] = 322560 kN
The part of the shear stiffness associated with the columns is;
KC = ∑(12EIC)/h2 = 3 × [(12 × 145833.33)/32] = 583333.32 kN
From the above, the reduction factor r can be defined as;
r = (KC)/(KB + KC) = (583333.32)/(322560 + 583333.32) = 0.6439
The original shear stiffness of the frame work can now be defined as;
K = KB × r = 322560 × 0.6439 = 207696.384 kN
With the above shear stiffness, the square of the fundamental frequency (fs2) of the framework due to shear deformation can be calculated as;
fs’2 = [1/(4H)2] × [rf2.K/m]
Where rf is the mass distribution factor given by:
rf = √n/(n + 2.06) = √30/(30 + 2.06) = 0.967 (Note that n = number of storeys = 30)
fs’2 = [1/(4 × 90)2] × [(0.9672 × 207696.384)/2100] = 7.136 x 10-4 Hz2
Ig = ∑(Ac,it2i)
Ig = (0.5 × 0.5) x (52 + 52) = 12.5 m4
The square of the fundamental frequency that belongs to this global second moment of area is;
fg2 = (0.313.rf2.EIg)/H4m = (0.313 × 0.9672 × 28 × 106 × 12.5)/(904 x 2100) = 7.435 x 10-4 Hz2
The effectiveness factor shows the extent the global bending deformation erodes the shear stiffness:
sf = √[(fg2)/(fs’2 + fg2)] = √[(7.435 x 10-4 )/(7.136 x 10-4 + 7.435 x 10-4)] = 0.714
With the effectiveness factor, the effective shear stiffness is;
Ke = sf2.K = 0.7142 x 207696.384 = 105882.7858 kN
The square of the fundamental frequency that belongs to the effective shear stiffness can now be calculated:
fs2 = [1/(4H)2] × [rf2.Ke/m] = [1/(4 × 90)2] × [(0.9672 × 105882.7858)/2100] = 3.638 x 10-4 Hz2
For the local bending stiffness (EI = EIc r), the sum of the second moments of area of the columns should be produced (and multiplied by reduction factor r). As the bays of the framework are identical, the second moment of area of one column is simply multiplied by n and r (the reduction factor):
I = r∑Ic = 0.6439 x 3 x 0.0052083 = 0.010 m4
The fundamental frequency which is associated with the local bending stiffness is defined by;
fb2 = (0.313.rf2.EI)/H4m = (0.313 × 0.9672 × 28 × 106 × 0.010)/(904 x 2100) = 5.948 x 10-7 Hz2
As a function of the non-dimensional parameter;
k = H√(Ke/EI) = 90√[105882.7858/(28 × 106 × 0.010)] = 55.345
The frequency parameter η can be obtained from Table 1;
Table 1: Frequency parameters η as a function of k (Zalka, 2013)
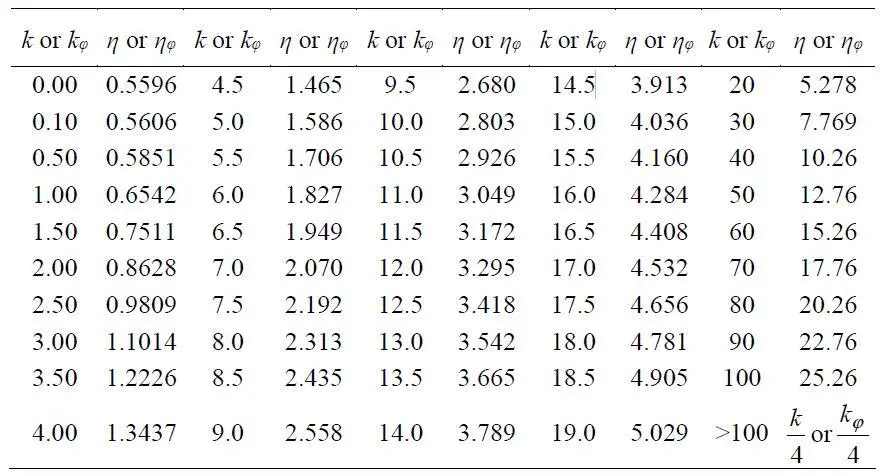
By interpolation;
η = 12.76 + [(55.344 – 50)/(60 – 50)] x (15.26 – 12.76) = 14.096
Finally, the fundamental frequency is;
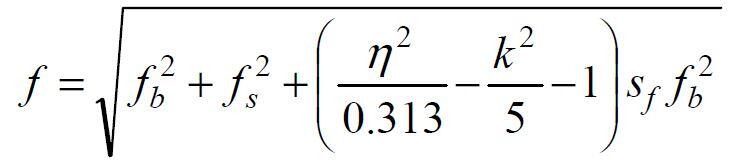
f = √{5.948 x 10-7 + 3.638 x 10-4 + [(14.0962/0.313) – (55.3452/5) – 1] x 0.714 x 5.948 x 10-7} = 0.019 Hz
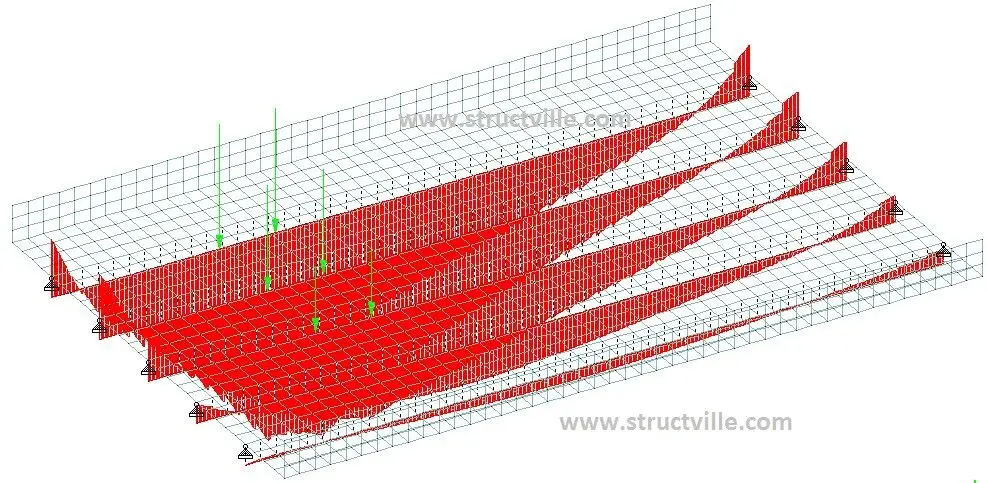
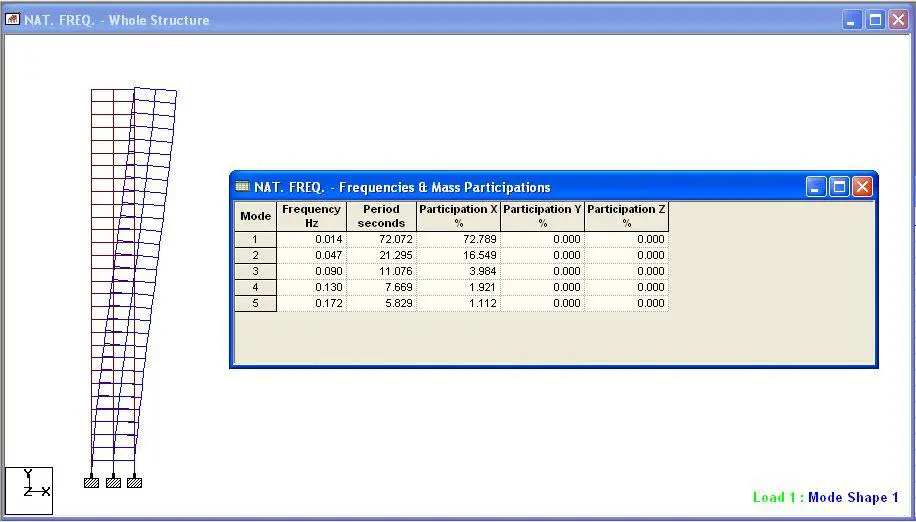
When this was modelled on Staad Pro, the natural frequency obtained was 0.014 Hz as shown in Figure 3.
Thank you for visiting today. Discussions on this post are welcome.
References
Zalka K. A. (2013): Structural Analysis of Regular Multi-storey Buildings. CRC Press – Taylor and Francis Group, USA