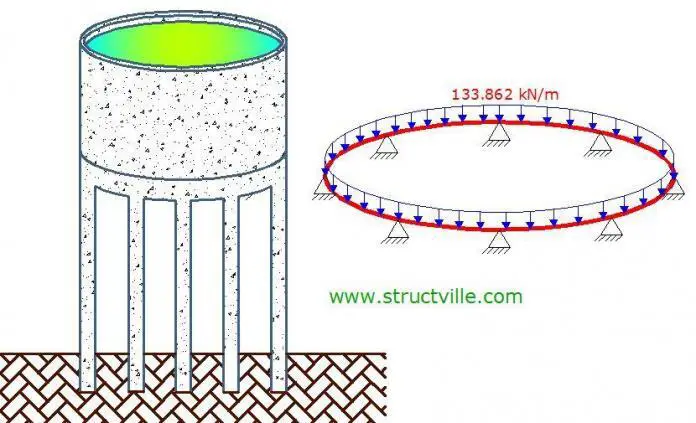
Beams that are curved in plan are often found in buildings, circular reservoirs, bridges, and other structures with curves. Curved beams always develop torsion (twisting) in addition to bending moment and shear forces because the center of gravity of loads acting normal to the plane of the structure lies outside the lines joining its supports. Therefore to maintain equilibrium in the structure, the supports of a curved beam must be fixed or continuous.
In this post, we are going to show in the most simplified manner, how to analyse continuous circular (ring) beams.

For ring beams;
Maximum Negative Moment at any support = K1wr2
Maximum Positive Moment at any span = K2wr2
Maximum Torsional Moment = K3wr2
Total load on each column (support reaction) R = wr(2θ)
Shear force at any support = R/2 = wrθ
The coefficients are given in the table below;
Solved Example
A cylindrical reservoir with a diameter of 6m is supported by a ring beam, which is supported on 8 equidistant columns. It is desired to analyse and design the ring beam to support the load from the superstructure.
The plan view of the structural disposition of the reservoir is shown below;
Load Analysis
(a) Geometry of sections
Dimension of beams = 450mm x 300mm
Dimension of column = ϕ300mm circular columns
Thickness of reservoir walls = 250mm
Thickness of reservoir slab = 250mm
(b) Density of materials
Density of stored material = 10 kN/m3
Density of concrete = 25 kN/m3
(c) Dead Loads
Weight of the walls = (25 kN/m3 × 0.25m × 4.75m × 18.849m) = 559.579 kN
Weight of bottom slab = (25 kN/m3 × 0.25m × 28.274m2) = 176.7125 kN
Weight of water stored = (10 kN/m3 × 4.5m × 23.758m2) = 1069.11 KN
Total = 1805.4015 kN
Let us transfer this load to the the ring beam based on the perimeter.
Perimeter of ring beam = πd = π × 6 = 18.849m
w = 1805.4015 kN / Perimeter of ring beam = 1805.4015 kN / 18.849m = 95.782 kN/m
Self weight of the beam = 25 kN/m3 × 0.3m × 0.45m = 3.375 kN/m
Total dead load on beam = 95.782 kN/m + 3.375 kN/m = 99.157 kN/m
Factoring the load on the beams at ultimate limit state = 1.35 × 99.157 kN/m = 133.862 kN/m
From the table above;
Number of supports (n) = 8
θ = π/n = 45°
K1 = 0.052
K2 = 0.026
K3 = 0.0040
Radius (r) = 3m
Maximum Negative Moment at the supports = K1wr2 = -0.052 × 133.862 × 32 = -62.647 KN.m
Maximum Positive Moment at the spans = K2wr2 = 0.026 × 133.862 × 32 = 31.323 KN.m
Maximum Torsional Moment = K3wr2 = 0.0040 × 133.862 × 32 = 4.819 KN.m
Shear force at the supports = R/2 = wrθ = 133.862 × 3 × (π/8) = 157.7 KN
Structural Design
Design strength of concrete fck = 35 N/mm2
Yield strength of reinforcement fyk = 500 N/mm2
Nominal cover to reinforcement = 30 mm
Span
MEd = 31.323 kN.m
Effective depth (d) = h – Cnom – ϕ/2 – ϕlinks
Assuming ϕ12 mm bars will be employed for the main bars, and ϕ8mm bars for the stirrups (links)
d = 450 – 30 – 6 – 8 = 406 mm
k = MEd/(fckbd2) = (31.323 × 106)/(35 × 300 × 4062) = 0.0181
Since k < 0.167, no compression reinforcement required
z = d[0.5+ √(0.25 – 0.882K) ] = z = d[0.5+ √(0.25 – 0.882(0.0181))] = 0.95d
As1 = MEd/(0.87yk z) = (31.323 × 106)/(0.87 × 500 × 0.95 × 406) = 186.69 mm2
Provide 3H12 mm BOT (ASprov = 339 mm2)
Supports
MEd = 62.647 KN.m
Effective depth (d) = h – Cnom – ϕ/2 – ϕlinks
Assuming ϕ16 mm bars will be employed for the main bars, and ϕ8mm bars for the stirrups (links)
d = 450 – 30 – 8 – 8 = 404 mm
k = MEd/(fckbd2) = (62.647 × 106)/(35 × 300 × 4042) = 0.0365
Since k < 0.167, no compression reinforcement required
z = d[0.5+ √(0.25 – 0.882K) ] = z = d[0.5+ √(0.25 – 0.882(0.0365))] = 0.95d
As1 = MEd/(0.87fyk z) = (62.647 × 106)/(0.87 × 500 × 0.95 × 404) = 375.23 mm2
Provide 2H16 mm TOP (ASprov = 402 mm2)
Interaction of shear and torsion
According to clause 6.3.2(2) of Eurocode 2, the effects of torsion and shear for both hollow and solid members may be superimposed, assuming the same value for the strut inclination θ. The limits for θ given in 6.2.3 (2) of EC2 are also fully applicable for the case of combined shear and torsion.
According to clause 6.3.2(4) of EC2, the maximum resistance of a member subjected to torsion and shear is limited by the capacity of the concrete struts. In order not to exceed this resistance the following condition should be satisfied:
TEd /TRd,max + VEd /VRd,max ≤ 1 ———- Equation (6.29 of EC2)
VEd = 157.7 KN
TEd = 4.819 kN.m
TRd,max = design torsional resistance moment
VRd,max = maximum shear resistance of the cross-section
Geometrical Properties for analysis of torsion
Area (A) = 300mm × 450mm = 135000 mm2
Perimeter (U) = 2(300) + 2(450) = 1500mm
Equivalent thickness = tef,i = A/U = 135000/1500 = 90mm
The equivalent thin wall section for the rectangular section is given below;
Ak = the area enclosed by the centre-lines of the connecting walls, including inner hollow areas = (450 – 90) × (300 – 90) = 75600 mm2
Uk = is the perimeter of the area Ak = 2(450 – 90) + 2(300 – 90) = 1140 mm
TRd,max = 2 v αcwfcdAktef,i sinθ cosθ
Assuming θ = 21.8° (cot θ = 2.5)
v = 0.6(1 – fck/250) = 0.6(1 – 35/250) = 0.516
fcd = (αcc × fck)/γc = (1 × 35)/1.5 = 23.33 N/mm2
TRd,max = 2 × 0.516 × 1.0 × 23.33 × 75600 × 90 × cos 21.8° × sin 21.8° × 10-6 = 56.485 KNm
VRd,c = [CRd,c.k.(100ρ1 fck)(1/3) + k1.σcp]bw.d
Where;
CRd,c = 0.18/γc = 0.18/1.5 = 0.12
k = 1 + √(200/d) = 1 + √(200/404) = 1.704 > 2.0, therefore, k = 1.702
ρ1 = As/bd = 402/(300 × 404) = 0.003317 < 0.02; K1 = 0.15
VRd,c = [0.12 × 1.704(100 × 0.003317 × 35 )(1/3)] 300 × 404 = 65469.358 N = 65.469 KN
Since VRd,c (65.469 KN) < VEd (157.7 KN), shear reinforcement is required.
The compression capacity of the compression strut (VRd,max) assuming θ = 21.8° (cot θ = 2.5)
VRd,max = (bw.z.v1.fcd)/(cotθ + tanθ)
V1 = 0.6(1 – fck/250) = 0.6(1 – 35/250) = 0.516
fcd = (αcc ) fck)/γc = (1 × 35)/1.5 = 23.33 N/mm2
Let z = 0.9d
VRd,max = [(300 × 0.9 × 404 × 0.516 × 23.333)/(2.5 + 0.4)] × 10-3 = 452.863 KN
Since VRd,c < VEd < VRd,max
Hence, Asw/S = VEd/(0.87Fykzcot θ) = 157700/(0.87 × 500 × 0.9 × 404 × 2.5 ) = 0.3988
Minimum shear reinforcement;
Asw/S = ρw,min × bw × sinα (α = 90° for vertical links)
ρw,min = (0.08 × √(fck))/fyk = (0.08 × √35)/500 = 0.0009465
Asw/S (min) = 0.0009465 × 300 × 1 = 0.2839
Since 0.2839 < 0.3988, adopt 0.3988
Maximum spacing of shear links = 0.75d = 0.75 × 404 = 303mm
Provide H8mm @ 250mm c/c (Asw/S = 0.402) Ok
Note that this link must be properly closed with adequate anchorage length, because it will assist in resisting torsion.
Design Considerations for Torsion
TEd /TRd,max + VEd /VRd,max ≤ 1
(4.891/56.485) + (157.7/453.863) = 0.434 < 1.0 Hence it is ok
However, note that the actual shear force at the point where torsion is maximum is actually less than the shear force at the support. The relationship above is an error but on the safe side.
The maximum torsion occurs at an angle of 9.5° from the support (see Table above). Therefore, the actual shear force at that section ( VEd) = Shear force at support – wrα
VEd = 157.7 – (133.862 × 3 × (9.5/180) × π) = 91.114 KN
Therefore for educational purposes, this is the shear force that should be used to check the shear-torsion interaction. A little consideration will show that VRd,max is constant all through the section, but VRd,c might vary depending on the longitudinal reinforcement provided at the section.
Rechecking the interaction above;
(4.891/56.485) + (91.114/453.863) = 0.287< 1.0 Hence it is ok
Area of transverse reinforcement to resist torsion
Asw/s = TEd/2Ak fyw,d cotθ
Asw/s = (4.819 × 106) / (2 × 135000 × 0.87 × 500 × 2.5) = 0.0164 < Asw/S (min)
Therefore, links provided for shear will be adequate for resisting torsion.
Area of longitudinal reinforcement to resist torsion
As1 = TEdUk cot θ / 2Ak fyd
As1 = (4.819 × 106 × 1140 × 2.5) / (2 × 75600 × 0.87 × 500) = 208 mm2
According to clause 6.3.2(4), in compressive chords, the longitudinal reinforcement may be reduced in proportion to the available compressive force. In tensile chords the longitudinal reinforcement for torsion should be added to the other reinforcement. The longitudinal reinforcement should generally be distributed over the length of side, but for smaller sections it may be concentrated at the ends of this length.
However, for the avoidance of doubt since no definition was given for what could be regarded as a ‘smaller section’, Provide 1H12mm bar at the middle of the section at both faces. The tensile and longitudinal reinforcement provided at the top and bottom of the section should be able to take care of the rest.
Further information
Nominal shear reinforcement is required in rectangular sections when;
TEd /TRd,c + VEd /VRd,c ≤ 1 ————– Equation (6.31 of EC2)
Where;
TRd,c is the value of the torsion cracking moment:
VRd,c is as defined above.
TRd,c = fctd⋅t⋅2Ak
τ = fctd = fctk /γc = 2.2/1.5 = 1.466 MPa (fctk deducted from Table [3.1 – EC2]).
It results therefore:
TRd,c = fctd⋅t⋅2Ak = 1.466 × 90 × 2 × 75600 × 10-6 = 19.949 kNm
From above calculations;
VRd,c = [0.12 × 1.704(100 × 0.003317 × 35 )(1/3)] 300 × 404 = 65469.358 N = 65.469 KN
(4.819/19.949) + 91.114/65.469) = 1.633 > 1.0 (Shear force at point of maximum torsion was used)
Therefore obviously this showed that shear reinforcement calculations were required.
References
Hassoun M.N., Al-Manaseer A. (2008): Structural Concrete Theory and Design (4th Edition). John Wile and Son Inc., New Jersey