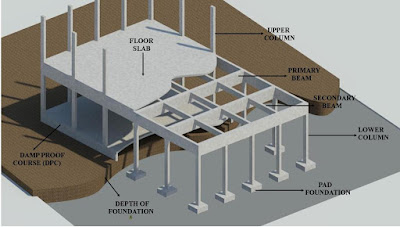
Explosives continue to be the terrorist’s preferred weapon, since they are destructive, relatively easy to obtain or fabricate, and still comparatively easy to move surreptitiously on the ground and by sea. Terrorists are also well aware that explosives produce fear in the general population far beyond the geographical location of their intended target.
On the 26th of August, 2011, a car bomb attacked the UN Building in Abuja, the capital of Nigeria, after breaking through two security barriers. The attack claimed about 21 lives, and wounded about 60. A wing of the building collapsed, and the ground floor was severely damaged.
There seems to be a sense of anxiety about the vulnerability of our buildings, bridges, tunnels, and utilities in the midst of numerous recognized international social and political instabilities, and given the potential for domestic groups and individuals to seek influence and create disruption by resorting to violent means. As a result, consultants designing buildings may be expected to provide advice and sometimes specific enhancements in response to quantifiable threats, as well as perceived vulnerabilities.
This post explains 21 basic things you should know about the design of blast resistant structures.
(1) An explosion is a violent thermochemical event
It involves supersonic detonation of an explosive material, violently expanding hot gases, and radiation of a shock front that has peak pressures that their magnitude is higher than those that buildings normally experience under any other loadings.
(2) Building an effective security and risk assessment team
A comprehensive risk assessment for blast-protection design involves close collaboration among city planners, architects, engineers, blast consultant subject matter experts, and law enforcement security professionals. In this group effort, collaborating professionals assess and select the security measures needed to detect, deter, prevent, defeat, mitigate, or recover from terrorists’ bomb attacks.
(3) Nature of blast impact
When the shock front radiating from a detonation strikes a building component, it is instantaneously reflected. This impact with a structure imparts momentum to exterior components of the building. The associated kinetic energy of the moving components must be absorbed or dissipated in order for them to survive. Generally, this is achieved by converting the kinetic energy of the moving facade component to strain energy in resisting elements.
(4) Mmmm… Not the whole structure may collapse
Structures as a whole generally are not pushed over by a common explosion. The overall mass of a structure is usually large enough to keep the kinetic energy imparted to the structure as a whole small enough that it can be absorbed by the multiple elements that would need to fail before the building topples.
(5) Stand-off distance (assumed location of explosion) is very important during assessment
Distance is the single most important asset to a structural engineer designing for blast resistance. The farther the explosion is from the structure, the lower are the effects that the structure must resist. Further, there often is merit to the construction of blast walls or line-of-sight barriers to add protection to a facility.
(6) Keep it confidential
When blast-resistant designs are for the security and safety of a facility/building in response to a threat of a malevolent attack, information about the assumed size and location of an explosion should be kept confidential. This information could be useful to an aggressor because it can reveal a strategy to overwhelm the designed defenses.
(7) Facades and fenestration can turn to missiles
The catastrophic fracturing of building materials such as facades, windows, glazing, and leakage of pressure in response to a blast often can be destructive to the interiors of buildings, even when the facades of those buildings are designed to resist the effects of an explosion. These can turn to missiles and occupant injuries are very possible should the design base explosion occur. Except when the most restrictive approaches to blast-resistant design are employed (e.g., with elastic response, so a building can remain functional). Airborne glass fragmentation continues to be identified as one of the most lethal aspects of building component responses to explosive events.
(8) Mass of a building and occupancy load can be beneficial
Blast effects usually are impulsive, meaning that they impart velocity to objects through development of momentum. With momentum being proportional to the product of mass and velocity, and kinetic energy being proportional to the product of mass and velocity squared, the larger the mass, the smaller the velocity and, hence, the smaller the energy that must be dissipated through strain. Therefore, additional mass to a building can be beneficial during an explosion.
(9) Provision for column failure and redistribution of stresses
Consultants designing for blast often provide for the possibility that a column will be severely damaged by an explosion, in spite of our best efforts at prevention. When consultants assume that a column has lost its strength, they must develop alternative load paths to prevent a collapse from progressing from the initially damaged column through the structure. One form of alternative resistance involves making beams strong and ductile enough to span over the area of damage, thereby redistributing the load on the damaged column to adjacent columns.
(10) Emergency response considerations
Designers working to enhance blast resistance must consider occupant exit and the needs of emergency responders. Blast resistance invariably includes windows with blast-resistant glass. By definition such glass is difficult to break. Firefighters will need to use special tools and engage unusual tactics to fight a fire in a building that is difficult to enter and vent, and that has features that inhibit extraction of trapped occupants. Designers might need to compensate for blast-resistance features, or enhance fire resistance.
(11) Magnitude of design pressure
Designers need to understand that the magnitudes of the pressures that an explosion imparts to a structure are highly dependent on the nature of the explosive material, the shape and casing of the device, the size and range of the explosion, the angle of incidence between the advancing shock front and the impacted surface, the presence of nearby surfaces that restrict the expansion of hot gases or that reflect pressure fronts, and the robustness of the impacted surface itself.
(12) Extensive damage of structures during a blast
In many explosions that cause extensive destruction, the damage develops in two phases:
(i) the energy released by the explosion degrades or destroys important structural elements, and
(ii) the damaged structure is unable to resist gravity and collapses beyond the area of initial damage.
(13) Individual elements are often treated as nonlinear SDOF elements
It is common in blast-resistant design to treat individual elements as single degree-of-freedom nonlinear systems. Performance is judged by comparison of response to limiting ductility factors (i.e., the ratio of peak displacement to displacement at yield) or support rotations, with the response calculated as though the structural element were subjected to a pressure function while isolated from other structural influences.
(14) Column integrity is the key
Typically, columns are the component whose integrity is key to sustaining the capability of a building’s structural system to survive a blast load. As such, attention to ensuring their survival should have the highest priority when the blast resistance of a building is to be upgraded.
(15) Beware of fragmentation
Injury and structural damage during an explosion may result not only from the direct pressure and impulse of an air blast, but also from the impact of flying objects called debris and fragmentation. Military weapons are typically explosive charges with some type of metal casing. Upon detonation, this case is ruptured and expelled as fragmentation at high velocity. Similarly, terrorist devices may be embedded with objects such as ball bearings or nails that will be ejected at high velocity. Other fragmentation may occur as objects interact with the blast wave created from a detonation and become airborne.
(16) Blast design is different from seismic design
The conventional approach to blast design is similar to that for seismic design, in two important ways:
(i) both loadings clearly are dynamic and, hence, solutions are energy-based, and
(ii) the way we detail structural elements determines the effective loads for which structures must be designed (meaning, we limit the strength we need to supply by allowing post-elastic behavior to dissipate energy).
However, blast loading, with its extremely fast rise time and usually short duration, is either dynamic or impulsive, depending on the nature of the explosive, its distance from the subject structure, and the level of confinement that the structure creates for the expanding hot gases.
(17) You may have to tolerate more damage
While we tolerate some damage in earthquakes, to dissipate energy, we usually allow more damage for blast events. We expect facades to sustain severe damage. In fact, blast-resistant design often tolerates breaching of the building enclosure (with attendant risk of fatalities) and even sometimes partial collapse of buildings.
(18) Reversal of stresses on floor slabs
Blast-related upward impulses on floor slabs can reverse force distributions in these structural elements. In systems that are not strong and ductile enough for these reversed forces, blast-induced deflection can fracture structural elements that are required to resist gravity loads. Hence, floor systems can fail after the direct effects of the blast pass and the slab falls back downward under the influence of gravity.
(19) Consider the effectiveness of post-event evacuation functions
While the immediate devastating effects of explosive events can be limited by protective design strategies, post-event evacuation functions and the subsequent activities of rescue and recovery are dependent upon the integrity of stairs, vertical transportation systems, power, lighting, voice communication, smoke management, and other systems. These systems can be placed out of service throughout the building or suffer disproportionate damage if they are not specifically designed in response to the project design basis explosive threats.
(20) Engage only licensed and experienced professionals
Blast resistance designers must be licensed design professionals who are knowledgeable in the principles of structural dynamics and experienced with their proper application in predicting the response of elements and systems to the types of loadings that result from an explosion, or they must work under the direct supervision of licensed professionals with appropriate training and experience.
(21) Threat Elimination remains the overall best option
Finally, elimination of the explosive event threat and the reduction of building materials and contents that have the opportunity to participate as fuel sources in the fire development triad of oxygen, fuel load, and an ignition source remains the most attractive, competent, and cost-effective process in developing designs for facilities on any site. However, based on the threat assessment, it may be unreasonable to assume that the facility will not be exposed to explosive event effects.
Disclaimer:
I do not claim ownership to the pictures used in this post. All pictures used here belong to their respective owners, of which it is a little bit impractical to recognise them all.
Information for this article is extracted from: Donald O. Dusenberry (2010): Handbook for Blast-Resistance Design of Buildings. John Wiley and Sons Inc.
Thank you for visiting, and may we remain determined in our struggle to make the world free from hatred, discrimination, violence, terrorism, poverty, and crime. God bless you as you discuss and share.
Your friend,
Ubani Obinna Ranks