Types of Structural Systems for Tall Buildings

By

-

December 23, 2020

Table of Contents

For a tall building to be successful, at a minimum, the structure should employ systems and materials appropriate to the building’s height and configuration. The structural system for a tall building must perform well and lend itself to efficient construction [1]. According to [1], a successful tall building should have the following features;

Create a friendly and inviting image that has positive values to building owners, users, and observers.
Fit the site, providing proper approaches with a congenial layout for people to live, work, and play.
Be energy-efficient, providing interior space with a controllable climate.
Allow flexibility in office layout with easily divisible space.
Offer space oriented to provide the best views.
Most of all, the building must make economic sense, without which none of the development would be a reality.

In the year 1969, Fazlur Khan classified structural systems for tall buildings relating to their heights with considerations for efficiency in the form of “Heights for Structural Systems” diagrams [2]. This marked the beginning of a new era of skyscraper revolution in terms of multiple structural systems [3].

Later, Khan upgraded these diagrams by way of modifications [4, 5]. He developed these schemes for both steel and concrete as can be seen from Figures 1 and 2 respectively [6]. Khan argued that the rigid frame that had dominated tall building design and construction so long was not the only system fitting for tall buildings.

khan 2 — **Fig 2:** *Classification of tall building structural systems for concrete [1]*

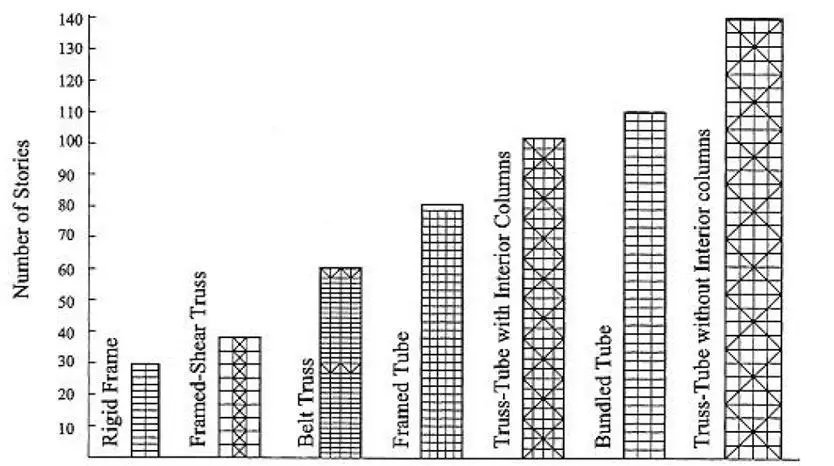
Bungale [1] also presented a table to show the appropriate structural system for reinforced concrete tall buildings. This is shown in Table 1.

Table 1: Appropriate structural systems for concrete tall building [1]

We are going to give a brief description of the various and popular structural systems for tall buildings in the sub-sections below. The structural system to be adopted in any design should be able to carry different types of loads, such as gravity, lateral, temperature, blast and impact loads. The drift of the tower should be kept within limits, such as H/500.

The structural systems usually adopted for high rise buildings are as follows;

Column and slab systems

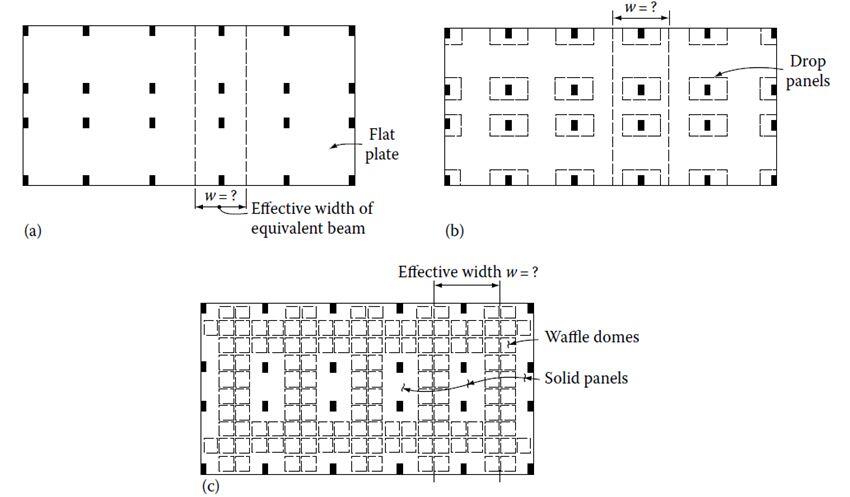
Concrete floors in tall buildings often consist of a two-way floor system such as a flat plate, flat slab, or a waffle system which can resist lateral loads (see Figure 3). In a flat plate system, the floor consists of a concrete slab of uniform thickness which frames directly into the columns. Two way flat slabs make use of either capitals in columns or drop panels in slab or both, requiring less than a flat plate because extra concrete is provided only at columns where the shears and moments are the greatest.

response of a flat slab to lateral load — **Fig 3**: Response of flat slab-frame to lateral load [1]

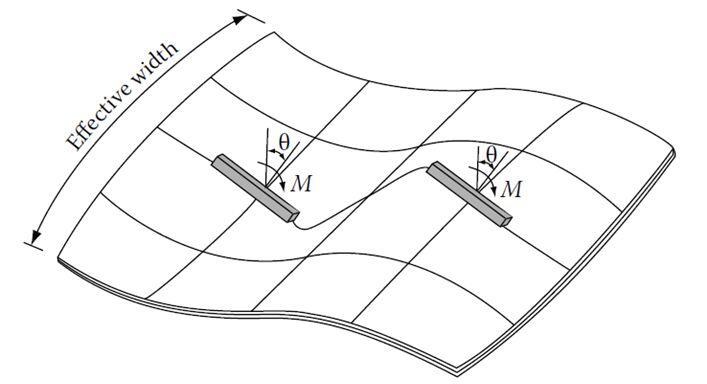
The waffle system is obtained using rows of joists at right angles to each other; the joists are commonly formed by square domes (see Figure 4). The domes are omitted around the columns to increase the moment and shear capacity of the slab [7]. Any of the three systems can be used to function as an integral part of the wind-resisting systems for buildings in the 10 to 20 storey range. The concept of an “effective width” is usually used in the analysis of such buildings subjected to lateral forces.

Typical floor systems for flat slab frames flat plate — **Fig 4:** Typical floor systems for flat slab-frames: (a) flat plate, (b) flat slab with drop panels, and (c) two-way waffle system [1]

Rigid Frames

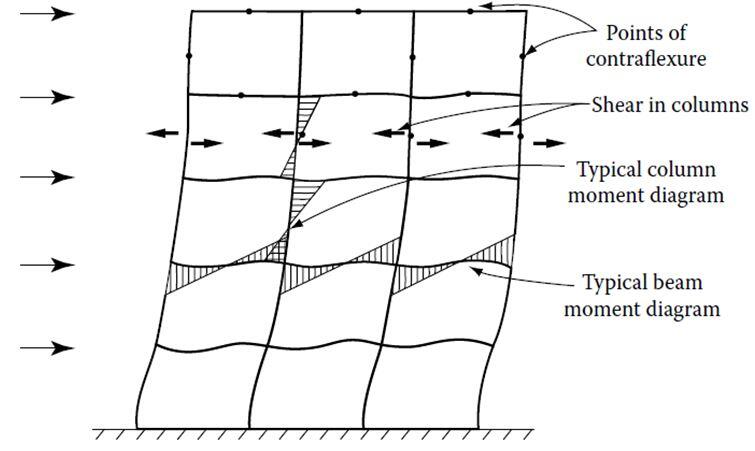
A rigid frame is characterized by the flexure of beams and columns and rotation at the joints. Interior rigid frames for office buildings are generally inefficient because;

(1) The number of columns in any given frame is limited due to leasing considerations and
(2) The beam depths are often limited by the floor-to-floor height.

However, frames located at the building exterior do not necessarily have these limitations. An efficient frame action can thus be developed by providing closely spaced columns and deep spandrels at the building exterior. A rigid-frame high-rise structure typically comprises of parallel or orthogonally arranged bents consisting of columns and girders with moment-resistant joints [8].

The continuity of the frame also increases resistance to gravity loading by reducing the positive moments in the girders [1]. The advantages of a rigid frame are the simplicity and convenience of its rectangular form. Its unobstructed arrangement, clear of structural walls, allows freedom internally for the layout and externally for the fenestration.

Rigid frames are considered economical for buildings of up to about 25 stories, above which their drift resistance is costly to control. If, however, a rigid frame is combined with shear walls, the resulting structure is very much stiffer so that its height potential may extend up to 50 stories or more [1].

The horizontal stiffness of a rigid frame is governed mainly by the bending resistance of the girders, the columns, and their connections, and in a tall frame, also by the axial rigidity of the columns (see Figure 5). The accumulated horizontal shear above any story of a rigid frame is resisted by shear in the columns of that story.

Rigid frame Forces and deformations — **Fig 5**: Rigid frame – Forces and deformations [1]

Rigid frame systems are not efficient for buildings over 30 storeys in height because the shear racking component of deflection caused by the bending of columns and girders causes the building to sway excessively [3].

Braced frames are a type of moment-resisting frames that have single diagonal x-braces and k-braces. Lattice and knee bracing are also used. Concrete braced frames are often not used, since shear walls are superior for construction and lateral resistance. Lattice bracing is used in pre-cast panel construction.

Steel braced frames are used in interior cores, so connections could easily be made with wall panels. Composite braced frames may have steel bracings in concrete bracings in steel frames. Concrete encasement of columns and composite floor beams has also been used.

Shear wall-Frame Systems

In this system, resistance to horizontal loading is provided by a combination of shear walls and rigid frames [9]. The shear walls are often placed around elevator and service cores while the frames with relatively deep spandrels occur at the building perimeter. When a wall–frame structure is loaded laterally, the distinctly different deflected forms of the walls and the frames can be quite effective in reducing the lateral deflections to the extent that buildings of up to 50 stories or more are economical [1].

The potential advantages of a wall–frame structure depend on the intensity of horizontal interaction, which is governed by the relative stiffness of the walls and frames, and the height of the structure. The taller the building and the stiffer the frames, the greater the interaction [10].

The interaction of frame and shear walls has been understood for quite some time, the classical mode of the interaction between a prismatic shear wall and a moment frame is that the frame basically deflects in a so-called shear mode while the shear wall predominantly responds by bending as a cantilever (see Figure 6).

shear wall frame interaction — **Fig 6:** Shear wall-frame interaction [1]

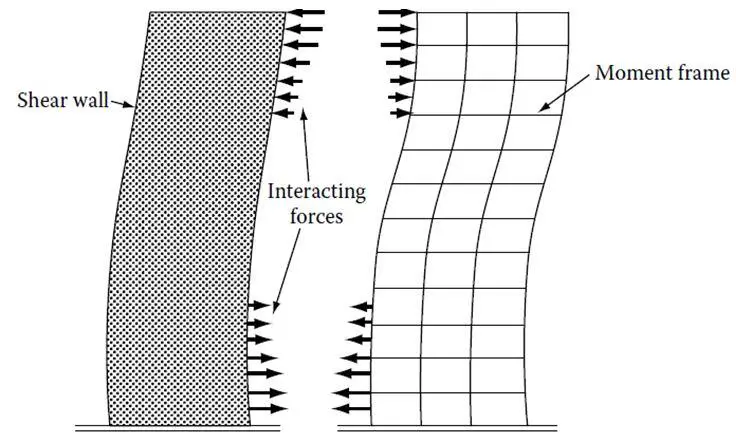
Compatibility of horizontal deflection introduces an interaction between the two systems which tends to impose a reverse curvature in the deflection pattern of the system. The combined structural action, therefore, depends on the relative rigidities of different elements used in the makeup of the lateral-load-resisting system.

The distribution of total wind shear to the individual shear walls and frames as given by the simple interaction diagram is valid only if one of the following two conditions is satisfied.

1. Each shear wall and frame must have constant stiffness properties throughout height of the building.
2. If stiffness properties vary over the height, the relative stiffness of each wall and frame must remain unchanged throughout the height of the building.

Shear Truss-Outrigger Braced Systems

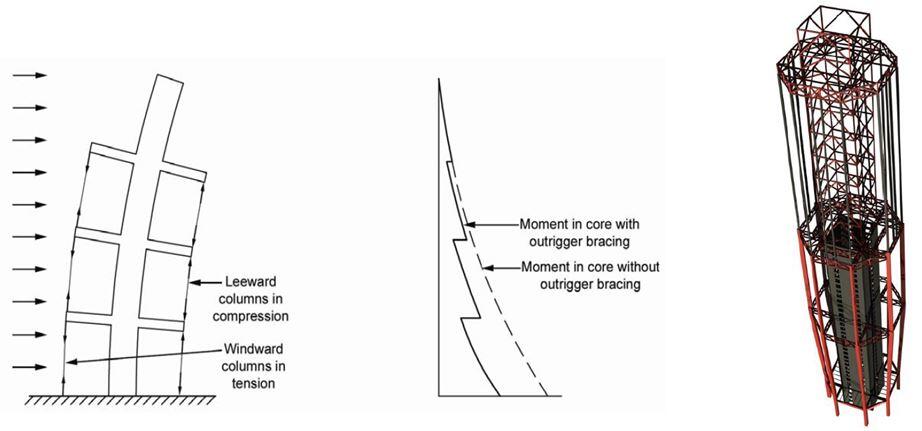
The structural arrangement for this system consists of a main concrete core connected to exterior columns by relatively stiff horizontal members such as one or two-story deep walls commonly referred to as outriggers. The core may be centrally located with outriggers extending on both sides or it may be located on one side of the building with outriggers extending to the building columns on one side [1].

The outrigger system is a development due to the desire to make inner cores and outer columns as one by linking them together at one or more levels with rigid arms – outriggers. It may be formed by any combination of steel, concrete or composite construction and reduce the structure’s internal overturning moment by up to 40 % compared to that of a free cantilever [10].

Multilevel outrigger systems can provide up to five times the moment resistance of a single outrigger system. Outrigger systems have been used for buildings up to 70 stories but the concept should hold for even higher buildings [11].

The basic structural response of the system is quite simple. When subjected to lateral loads, the column-restrained outriggers resist the rotation of the core, causing the lateral deflections and moments in the core to be smaller than if the freestanding core alone resisted the loading as shown in Figure 7 [3].

The external moment is resisted not by bending of the core alone, but also by the axial tension and compression of the exterior columns connected to the outriggers. As a result, the effective depth of the structure for resisting bending is increased when the core flexes as a vertical cantilever, by the development of tension in the windward columns, and by compression in the leeward columns.

**Fig 17**: Core supported outrigger structure [3]

Framed-Tube System

In its simplest terms, a framed tube can be defined as a three-dimensional system that engages the entire building perimeter to resist lateral loads [1]. A necessary requirement to create a wall-like three-dimensional structure is to place columns on the building exterior relatively close to each other, joined by deep spandrel girders as shown in Figure 8.

**Fig. 8:** Frame tube building. (a) Schematic plan and (b) isometric view [1]

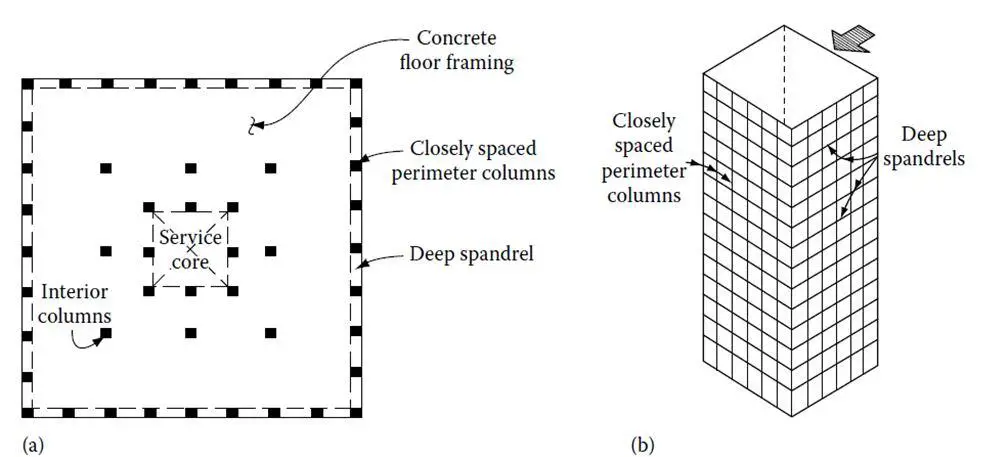
The system works quite efficiently as a hollow vertical cantilever. However, lateral drift due to the axial displacement of the columns—commonly referred to as chord drift—and web drift, caused by shear and bending deformations of the spandrels and columns, may be quite large depending upon the tube geometry.

In framed tube systems, the “strong” bending direction of the columns is typically aligned along the face of the building, in contrast to a typical transverse rigid frame where it is aligned perpendicular to the face. The frames parallel to the lateral load act as webs of the perforated tube, while the frames normal to the load act as the flanges.

When subjected to bending, the columns on opposite sides of the neutral axis of the tube are subjected to tensile and compressive forces. In addition, the frames parallel to the direction of the lateral load are subjected to the in-plane bending and the shearing forces associated with an independent rigid frame action.

Trussed Tube Systems

A trussed tube system improves the efficiency of the framed tube by increasing its potential for use in taller buildings and allowing greater spacing between the columns. This is achieved by adding diagonal bracing at the faces of the tube as shown in Figure 9 to virtually eliminate the shear lag in both the flange and web frames [1].

hnn — **Fig. 9**: Trussed tube System [1]

The framed tube, as discussed previously, even with its close spacing of columns is somewhat flexible because the high axial stresses in the columns cannot be transferred effectively around the corners. For maximum efficiency, the tube should respond to lateral loads with the purity of a cantilever, with compression and tension forces spread uniformly across the windward and leeward faces.

The framed tube, however, behaves more like a thin-walled tube with openings. The axial forces tend to diminish as they travel around the corners, with the result that the columns in the middle of the windward and leeward faces may not sustain their fair share of compressive and tensile forces. An example of an application is the Onterie Centre building in Chicago (Figure 10).

onterie — **Fig. 10**: Onterie Center Building, Chicago (www.skyscrapercentre.com)

Bundled Tube Systems

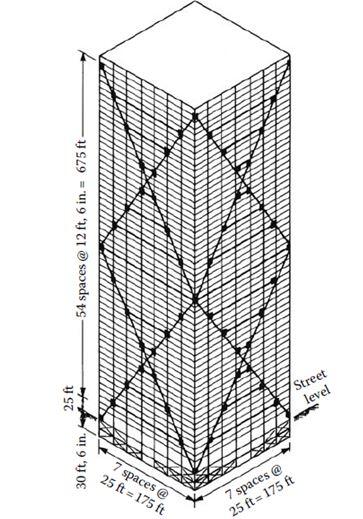
The bundled tube structure consists of four parallel rigid frames in each orthogonal direction, interconnected to form nine bundled tubes (see Figure 11). The principle is the same as for the single tube structure where the frames in the horizontal load direction act as webs and the perpendicular frames acts as flanges.

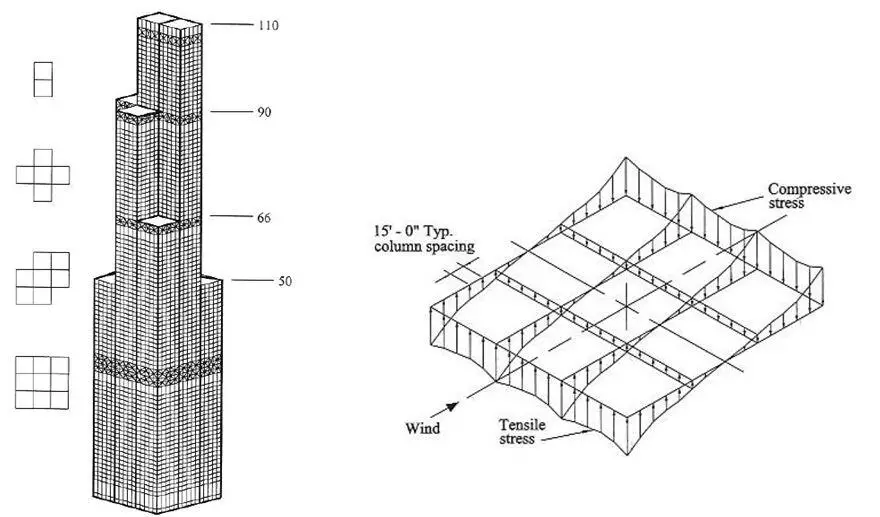
By introducing the internal webs the shear lag is drastically reduced and as a result the stresses in the columns are more evenly distributed and their contribution to the lateral stiffness is more significant. This allows for the columns to be spaced further apart and to be less striking. In essence, the underlying principle to achieve a bundled tube response is to connect two or more individual tubes into a single bundle. The main purpose is to decrease shear lag effects.

References

[1] Bungale S. T. (2010): Reinforced Concrete Design of Tall Buildings. CRC Press, Taylor and Francis Group
[2] Khan, F.R. (1969): Recent structural systems in steel for high-rise buildings. In Proceedings of the British Constructional Steelwork Association Conference on Steel in Architecture. London: British Constructional Steelwork Association.
[3] Ali M.M., and Moon K.S. (2007): Structural developments in tall buildings: Current trends and future prospects. Architectural Science Review 50(3):205-223
[4] Khan, F.R. (1972): Influence of design criteria on selection of structural systems for tall buildings, In Proceedings of the Canadian Structural Engineering Conference. Toronto: Canadian Steel Industries Construction Council, 1-15.
[5] Khan, F.R. (1973): Evolution of structural systems for high-rise buildings in steel and concrete. In J. Kozak (Ed.), Tall Buildings in the Middle and East Europe: Proceedings of the 10th Regional Conference on Tall Buildings-Planning, Design and Construction. Bratislava: Czechoslovak Scientific and Technical Association
[6] Ali, M.M. (2001): Art of the Skyscraper: The Genius of Fazlur Khan. New York: Rizzoli.
[7] Reddy S.V.B., and Eadukondalu M. (2018): Study of the lateral structural systems in tall buildings. International Journal of Applied Engineering Research 13(15):11738 – 11754
[8] Zalka K. A. (2013): Structural Analysis of Regular Multi-storey Buildings. CRC Press – Taylor and Francis Group, USA
[9] Aginam C.H., Chidolue C.A., and Ubani O.U. (2015): Effect of Planar Solid shear wall-frame arrangement on the deformation behaviour of multi-story frames. IOSR Journal of Mechanical and Civil Engineering 12(1):98-105
[10] Sandelin C. and Bujadev E. (2013): The stabilization of high-rise buildings: An evaluation of the tubed mega frame concept. Dissertation submitted to the Department of Engineering Science, Applied Mechanics, Civil Engineering, Uppsala University
[11] Hallebrand E., and Jakobsson W. (2016): Structural design of high-rise buildings. M.Sc thesis presented to the Department of Construction Sciences (Division of structural mechanics), Lund University, Sweden

Out-of-Plane Two-Way Bending Analysis of Unreinforced Masonry Walls

By

Ubani Obinna

-

December 21, 2020

Masonry is defined as an assemblage of masonry units (blocks, bricks, etc) laid in a specified pattern and joined together with mortar. They are usually used in components subjected to compressive loads such as walls, columns, arches, domes, vaults, etc. On other hand, masonry elements have limited capacity to support horizontal loads and bending moments.

Within the last decades, the efficiency of masonry units has increased due to higher allowable stresses, and refined possibilities in design. This, therefore, calls for more precision in the analysis, construction, and production of masonry to be used as structural members. This brings the design of masonry walls as a task of civil engineers.

Previous researches have shown that the out-of-plane (OOP) two-way bending failure of structural components can be one of the most predominant failure mechanisms in unreinforced masonry (URM) buildings. This is according to a submission from research carried out at the Faculty of Civil Engineering and Geosciences, Delft University of Technology, Netherlands. The study was published in the Elsevier – Structures journal in December 2020.

According to the researchers, extensive analytical formulations have been well developed for one-way vertically spanning walls, while analytical formulations for URM walls in OOP two-way bending require further improvement in accuracy and extension for the application range.

In order to bridge this knowledge gap, the researchers carried out an international testing campaign on a dataset of 46 testing specimens, in order to evaluate current analytical formulations. The current analytical formulations (codes of practice) used for the evaluation of the test specimens are;

EN 1996-1-1:2005-Eurocode 6 (based on the yield line method),
Australian Standard AS3700:2018 (based on the virtual work method), and
two other virtual work formulations related to AS3700 (W2006 and G2019)

The analytical formulations that have been developed in the past decades were incorporated into design standards to assess the wall capacity in engineering practice. The current analytical formulations are mainly based on the yield line method or on the virtual work method.

The underlying assumptions used in the development of the yield line method are:

masonry is simplified as a homogeneous material;
all cracks develop simultaneously;
the force capacity is calculated from the equilibrium between the applied forces and the reaction forces along cracking lines.

One drawback of the yield line method is that some crucial factors such as bonding patterns are neglected since masonry is considered as a homogenous material. This can affect the crack pattern therefore possibly resulting in misevaluation. Another drawback of the yield line method is that all cracks are assumed to develop concurrently, which can lead to inaccuracy for calculating the force capacity since contributions of all cracks are taken into account.

Another category of analytical formulations originates from the virtual work method. The major underlying assumptions of the virtual work method are:

the contributions from horizontal cracks are neglected;
diagonal cracks start right from the wall corners;
the cracking pattern is assumed to follow the mortar joints and is determined by the aspect ratios of the units and of the wall; horizontal and diagonal bending moment capacities are calculated independently;
the virtual work done by external loads is equal to the strain energy along cracking lines in pre-assumed cracking patterns

yield line of masonry walls — **Figure 1**: Classic pre-assumed cracking patterns used in formulations based on the virtual work method [1]

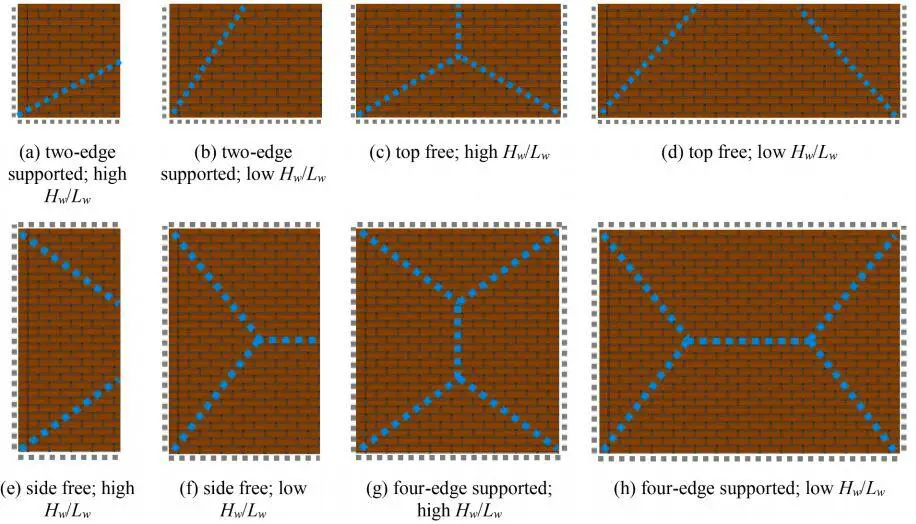
Additionally, the virtual work method provides coefficients and formulas to consider the presence of openings, while the yield line method does not. It is important to note that the afore-mentioned formulations are all force-based methods.

The dataset of the study carried out consists of tests performed mostly on clay brick and calcium silicate (CS) brick masonry walls. 37 out of 46 testing specimens were subjected to quasi-static cyclic loading, while the others to dynamic loading.

The testing configuration of the specimens — **Figure 2**: The testing configuration of the testing specimens [1]

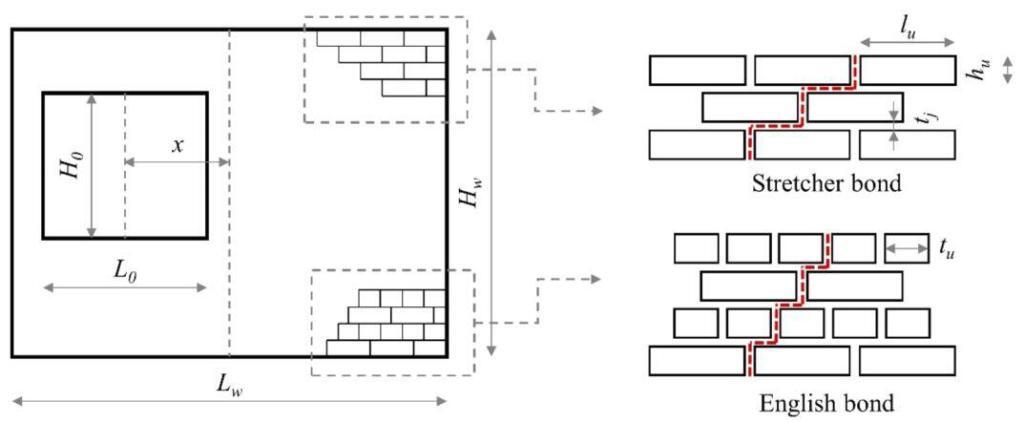
Eurocode 6 evaluates the force capacity w of a wall by following equation;

w = [(f_x1 + σ_d)Z]/μα₂L_w² —— (1)

where the flexural strength ratio μ is defined as:

μ = (f_x1+ σ_d)/f_x2 —— (2)

Where;
f_x1 and f_x2 are the flexural strength of masonry obtained for planes of failure parallel to and perpendicular to the bed joints,
respectively;
σ_d is the vertical compressive stress at a specific height of the wall caused by self-weight and pre-compression σ;
Z is the section modulus of the wall;
α₂ is the bending moment coefficient

The formulations AS3700, W2006 and G2019 assess the force capacity w of a wall by the following equation:

w = [2α_f /L_d²] (k₁M_h + k₂M_d) —— (3)

with the components of Eq. (3):

G = 2(h_u + t_j)/(l_u + t_j) —— (4)
α = GL_d/H_d ——(5)

where;
H_d and L_d are the design height and design length of the wall, respectively
G is the assumed slope of the crack line;
α is the slope factor that identifies the expected cracking pattern including a vertical central crack in the case α < 1, or a horizontal central crack in the case α ≥ 1;
α_f, k₁ and k₂ are coefficients determined by the presence of the openings, the slope factor α and the number of supported vertical edges
M_h and M_d are the horizontal and the diagonal bending moment capacity of masonry, respectively.

The equations for M_d and M_h are provided in the research article accordingly.

To compare the accuracy of the formulations, the tested force capacity from the dataset was predicted according to the equations of the analytical formulations. Lower and upper bounds for each testing specimen were calculated. The lower bound of the force capacity was estimated by considering the wall hinged on all sides in EC6 or assuming R_f = 0 in the other formulations; the upper bound of the force capacity was estimated by considering the wall clamped on all sides in EC6 or assuming R_f = 1 for the other formulations.

The comparison showed that EC6 has an incorrect prediction rate of 58.7% with the highest overestimation rate of 47.8%. W2006 and G2019 have incorrect prediction rates of 71.7% and 65.2%, respectively. Both these two formulations tend to underestimate the force capacity. AS3700 provides the lowest incorrect prediction rate of 56.6%. Also, the incorrect prediction rate on walls without openings of AS3700 is the lowest.

Table 1: Percentage of incorrect predictions for the considered dataset [1]

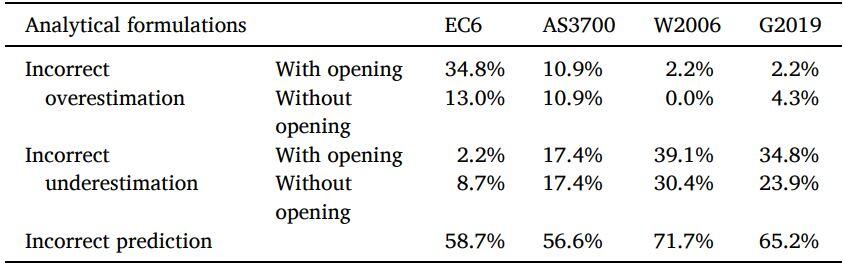
Nevertheless, the accuracy of AS3700 requires further improvement considering 21.8% and 34.8% of testing specimens are overestimated and underestimated, respectively. The formulations based on the virtual work method provide close incorrect prediction rates for walls with and without openings.

In conclusion, the formulations based on the virtual work method returned the most accurate predictions for the testing specimens evaluated in the study, especially for partially clamped walls and walls with openings. Nevertheless, drawbacks and limitations were revealed when analytical formulations were applied to assess the influence of crucial factors on the force capacity such as precompression of the wall, bonding pattern, boundary conditions, material properties, area of openings, and eccentricity of load.

To improve the accuracy and application range of the analytical formulations, further study is suggested regarding the influence of above-mentioned crucial factors on the wall failure mechanisms and quantifying the relations between the force capacity and the crucial factors.

Disclaimer
The contents of this article are culled from [Lang-Zi Chang, Francesco Messali, Rita Esposito (2020): Capacity of unreinforced masonry walls in out-of-plane two-way bending: A review of analytical formulations. Structures 28 (2020) 2341-2477] and does not belong to www.structville.com. It has been presented here in accordance to the requirements of open access articles under the CC BY license (http://creativecommons.org/licenses/by/4.0/)

References
[1] Lang-Zi Chang, Francesco Messali, Rita Esposito (2020): Capacity of unreinforced masonry walls in out-of-plane two-way bending: A review of analytical formulations. Structures 28 (2020) 2341-2477 https://doi.org/10.1016/j.istruc.2020.10.060

Design of Pile Foundation

By

Ubani Obinna

-

December 20, 2020

Table of Contents

Deep foundations are employed when the soil stratum beneath the structure is not capable of supporting the load with a tolerable settlement or adequate safety against shear failure. The two common types of deep foundations are well foundations (or caissons) and pile foundations. Piles are relatively long, slender members that are driven into the ground or cast-in-situ. The design of pile foundation involves providing adequate pile type, size, depth, and number to support the superstructure load without excessive settlement and bearing capacity failure. Deep foundations are more expensive and technical than shallow foundations.

Pile Foundations can be used in the following cases;

When the upper soil layer(s) is (are) highly compressible and too weak to support the load transmitted by the superstructure, piles are used to transmit the load to underlying bedrock or a stronger soil layer. When bedrock is not encountered at a reasonable depth below the ground surface, piles are used to transmit the structural load to the soil gradually. The resistance to the applied structural load is derived mainly from the frictional resistance developed at the soil–pile interface.
When subjected to horizontal forces, pile foundations resist by bending while still supporting the vertical load transmitted by the superstructure. This situation is generally encountered in the design and construction of earth-retaining structures and foundations of tall structures that are subjected to strong wind and/or earthquake forces.
In many cases, the soils at the site of a proposed structure may be expansive and collapsible. These soils may extend to a great depth below the ground surface. Expansive soils swell and shrink as the moisture content increases and decreases, and the swelling pressure of such soils can be considerable. If shallow foundations are used, the structure may suffer considerable damage.
The foundations of some structures, such as transmission towers, offshore platforms, and basement mats below the water table, are subjected to uplifting forces. Piles are sometimes used for these foundations to resist the uplifting force.
Bridge abutments and piers are usually constructed over pile foundations to avoid the possible loss of bearing capacity that a shallow foundation might suffer because of soil erosion at the ground surface

Classification of Piles

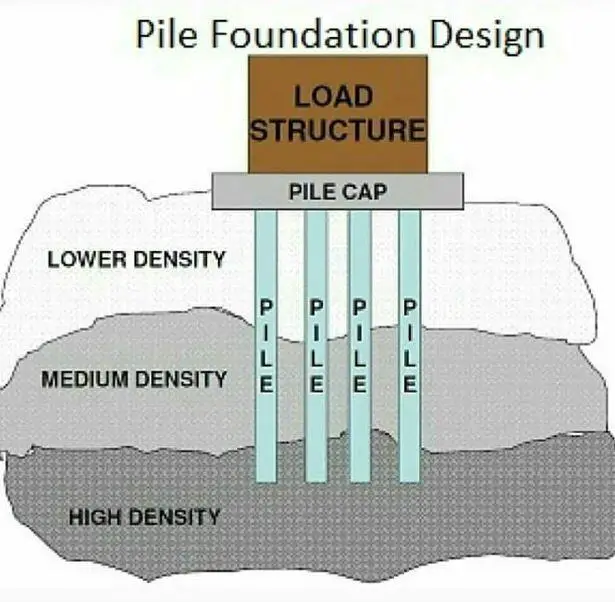
Piles may be classified in a number of ways based on different criteria:

(a) Function or action
(b) Composition and material
(c) Method of installation

Classification Based on Function or Action

Piles may be classified as follows based on the function or action:

End-bearing piles
Used to transfer load through the pile tip to a suitable bearing stratum, passing soft soil or water.

Friction piles
Used to transfer loads to a depth in a frictional material by means of skin friction along the surface area of the pile.

Tension or uplift piles
Uplift piles are used to anchor structures subjected to uplift due to hydrostatic pressure or to overturning moment due to horizontal forces.

Compaction piles
Compaction piles are used to compact loose granular soils in order to increase the bearing capacity. Since they are not required to carry any load, the material may not be required to be strong; in fact, sand may be used to form the pile. The pile tube, driven to compact the soil, is gradually taken out and sand is filled in its place thus forming a ‘sand pile’.

Anchor piles
These piles are used to provide anchorage against horizontal pull from sheetpiling or water.

Fender piles
They are used to protect water-front structures against impact from ships or other floating objects.

Sheet piles
Sheet piles are commonly used as bulkheads, or cut-offs to reduce seepage and uplift in hydraulic structures.

Batter piles
Used to resist horizontal and inclined forces, especially in water front structures.

Laterally-loaded piles
Used to support retaining walls, bridges, dams, and wharves and as fenders for harbour construction.

Classification Based on Material and Composition

Piles may be classified as follows based on material and composition:

Timber piles
These are made of timber of sound quality. Length may be up to about 8 m; splicing is adopted for greater lengths. Diameter may be from 30 to 40 cm. Timber piles perform well either in fully dry condition or submerged condition. Alternate wet and dry conditions can reduce the life of a timber pile; to overcome this, creosoting is adopted. Maximum design load is about 250 kN.

Steel piles
These are usually H-piles (rolled H-shape), pipe piles, or sheet piles (rolled sections of regular shapes). They may carry loads up to 1000 kN or more.

RAKER H PILES — **Figure 2**: Steel H-section piles

Concrete piles
These may be ‘precast’ or ‘cast-in-situ’. Precast piles are reinforced to withstand handling stresses. They require space for casting and storage, more time to cure and heavy equipment for handling and driving. Cast-in-situ piles are installed by pre-excavation, thus eliminating vibration due to driving and handling.

precast concrete piles — **Figure 3***: Precast concrete piles*

Composite piles
These may be made of either concrete and timber or concrete and steel. These are considered suitable when the upper part of the pile is to project above the water table. The lower portion may be of untreated timber and the upper portion of concrete. Otherwise, the lower portion may be of steel and the upper one of concrete.

Classification Based on Method of Installation

Piles may also be classified as follows based on the method of installation:

Driven piles
Timber, steel, or precast concrete piles may be driven into position either vertically or at an inclination. If inclined they are termed ‘batter’ or ‘raking’ piles. Pile hammers and pile-driving equipment are used for driving piles.

Cast-in-situ piles
Only concrete piles can be cast-in-situ. Holes are drilled and these are filled with concrete. These may be straight-bored piles or may be ‘under-reamed’ with one or more bulbs at intervals. Reinforcements may be used according to the requirements.

Driven and cast-in-situ piles
This is a combination of both types. Casing or shell may be used. The Franki pile falls in this category.

However, the commonest type of pile foundation in Nigeria is bored piles using continuous flight auger (CFA).

Design of Pile Foundation

Section 7 of EN 1997-1:2004 is dedicated to the geotechnical design of pile foundations. There are some design standards that are dedicated to the design and construction of pile foundations. A design standard that is referred to is the part of Eurocode 3 for the structural design of steel piles:

EN 1993-5: Eurocode 3, Part 5: Design of Steel Structures – Piling

Other standards that can be referred to for the execution of piling work are;

EN 1536:1999 – Bored Piles
EN 12063:1999 – Sheet pile walls
EN 12699:2000 – Displacement piles
EN 14199:2005 – Micropiles

Approaches to the design of pile foundations

According to clause 7.4(1)P of EN 1997-1, the design of piles shall be based on one of the following approaches:

The results of static load tests, which have been demonstrated, by means of calculations or otherwise, to be consistent with other relevant experience
Empirical or analytical calculation methods whose validity has been demonstrated by static load tests in comparable situations
The results of dynamic load tests whose validity has been demonstrated by static load tests in comparable situations
The observed performance of a comparable pile foundation provided that this approach is supported by the results of site investigation and ground testing.

Static load test is the best way of verifying the load-carrying capacity of piles, however, it is not very attractive because it is expensive and time-consuming. Traditionally, engineers have designed pile foundations based on calculations from theoretical soil mechanics. The commonest approach is to divide the soil into layers and assign soil properties to each layer. The most important soil parameters given to each layer is cohesion (C) and angle internal friction (ϕ). These two properties will enable the quick determination of the bearing capacity factors for evaluation of the load-carrying capacity of the pile.

From the soil profile, the shaft friction on the pile from different layers is summed up to obtain the total shaft friction resistance of the pile. The base resistance of the pile is also obtained based on the soil properties of the layer receiving the tip of the pile.

Design of pile foundation in layered soil — **Figure 4***: Pile in a layered soil*

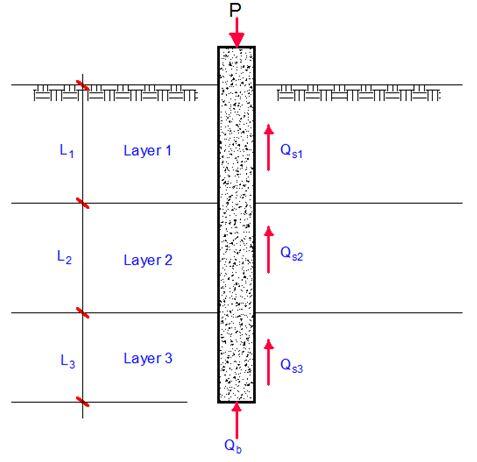
Hence ultimate pile resistance Q_u;

Q_u = ∑Q_s + Q_b —— (1)

Q_s = Shaft resistance = q_sA_s
Q_b= Base resistance = q_bA_b

Where q_s is the unit shaft resistance of the pile and A_s is the surface area of the pile for which q_s is applicable. A_b is the cross-sectional area of the base of the pile while q_b is the base resistance.

For pile in cohesionless soil (C = 0)
Q_s = q₀K_stanδA_s —— (2)

For pile in cohesive soil (ϕ = 0)
Q_s = αC_uA_s —— (3)

Where;
q₀ is the average effective overburden pressure over the embedded depth of the pile for which K_stanδ is applicable.
K_s is the lateral earth pressure coefficient
δ is the angle of wall friction
C_u is the average undrained shear strength of clay along the shaft
α is the adhesion factor.

Typical values of δ and K_s are given in the table below;

On the other hand, the typical equations for obtaining the base resistance of a single pile are given below;

Q_b = Base resistance = q_bA_b
Where q_b is the unit base resistance of the pile and A_b is the area of the pile base.

For pile in cohesionless soil (C = 0)
Q_b = q₀N_qA_b —— (4)

For pile in cohesive soil (ϕ = 0)
Q_b = c_bN_cA_b —— (5)

For pile in c-ϕ soil;
Q_b = (c_bN_c + q₀N_q)A_b —— (6)

Where N_q and N_c are bearing capacity factors.

Therefore for a design to be considered acceptable, the applied load ≤ Ultimate Capacity/Factor of Safety. The factor of safety usually varies between 2.0 and 3.0 and depends on the quality of ground investigation carried out.

Pile Foundation Design to Eurocode 7

EN 1997-1:2004 allows the resistance of individual piles to be determined from;

static pile formulae based on ground parameters
direct formulae based on the results of field test
the results of static pile load test
the results of dynamic impact tests
pile driving formulae, and
wave equation analysis

According to clause 7.6.2.1 (1)P, to demonstrate that the pile foundation will support the design load with adequate safety against compressive failure, the following inequality shall be satisfied for all ultimate limit state load cases and load combinations:

F_c,d ≤ R_c,d —— (7)

Where F_c,d is the design axial load on the pile, while R_c,d is the compressive resistance of the pile. F_c,d should include the weight of the pile itself, and Rc,d should include the overburden pressure of the soil at the foundation base. However, these two items may be disregarded if they cancel approximately. They need not cancel if the downdrag is significant, or when the soil is very light, or when the pile extends above the ground surface.

For piles in group, the design resistance shall be taken as the lesser of the compressive resistance of the piles acting individually, and the compressive resistance of the piles acting as a group (block capacity). According to clause 7.6.2.1(4), the compressive resistance of the pile group acting as a block may be calculated by treating the block as a single pile of large diameter.

Static pile formulae based on ground parameters

Methods for assessing the compressive resistance of a pile foundation from ground test results shall have been established from pile load tests and from comparable experience. Generally, the compressive resistance of the pile shall be derived from;

R_c,d = R_b,d + R_s,d —— (8)

Where;
R_b,d = R_b,k/γ_b
R_s,d = R_s,k/γ_s

The values of the partial factors may be set by the National annex. The recommended values for persistent and transient situations are given in Table A6, A7, and A8 of EN 1997-1:2004 for driven, bored, and CFA piles respectively;

Table 1 (Table A6): Partial resistance factors (γ_R) for driven piles

Resistance	Symbol	R1	R2	R3	R4
Base	γ_b	1.0	1.1	1.0	1.3
Shaft (compression)	γ_s	1.0	1.1	1.0	1.3
Total/combined (compression)	γ_t	1.0	1.1	1.0	1.3
Shaft in tension	γ_s;t	1.25	1.15	1.1	1.6

Table 2 (Table A7): Partial resistance factors (γ_R) for bored piles

Resistance	Symbol	R1	R2	R3	R4
Base	γ_b	1.25	1.1	1.0	1.6
Shaft (compression)	γ_s	1.0	1.1	1.0	1.3
Total/combined (compression)	γ_t	1.15	1.1	1.0	1.5
Shaft in tension	γ_s;t	1.25	1.15	1.1	1.6

Table 3 (Table A8): Partial resistance factors (γ_R) for continuous flight auger (CFA) piles

Resistance	Symbol	R1	R2	R3	R4
Base	γ_b	1.1	1.1	1.0	1.45
Shaft (compression)	γ_s	1.0	1.1	1.0	1.3
Total/combined (compression)	γ_t	1.11	1.1	1.0	1.4
Shaft in tension	γ_s;t	1.25	1.15	1.1	1.6

The characteristic values R_b,k and R_s,k shall be determined from;

R_c,k = R_b,k + R_s,k = (R_b,cal + R_s,cal)/ξ = R_c,cal/ξ = min[R_c,cal(mean)/ξ₃; R_c,cal(min)/ξ₄] —— (9)

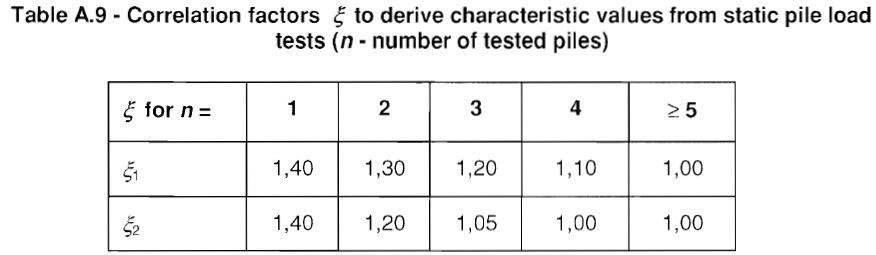
where ξ₃ and ξ₄ are correlation factors that depend on the number of profiles of tests, n. The values of the correlation factors may be set by the National annex. The recommended values are given in Table A10 of EN 1997-1:2004. For structures with sufficient stiffness and strength to transfer loads from “weak” to “strong” piles, the factors ξ₃ and ξ₄ may be divided by 1.1, provided that is never less than 1.0.

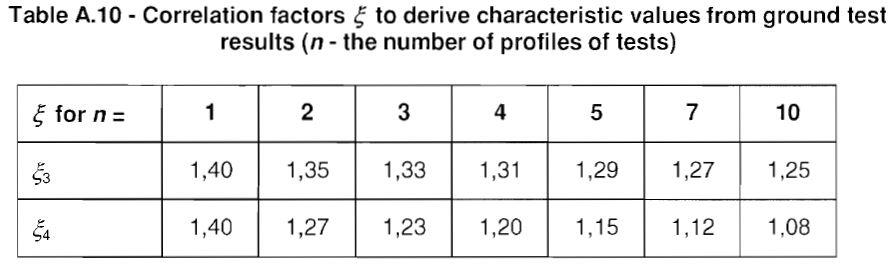
The characteristic values may be obtained by calculating:
R_b,k = A_b q_b,k —— (11)
R_s,k = ∑A_s,i q_s,i,k —— (12)

where q_b,k and q_s,i,k are the characteristic values of base resistance and shaft friction in the various strata, obtained from values of ground parameters.

To estimate pile shaft friction and end bearing from ground parameters, the following relationships may be applied;

Cohesionless soils;
q_s,k = σ_v‘k_stanδ —— (13)
q_b,k = σ_v‘ N_q —— (14)

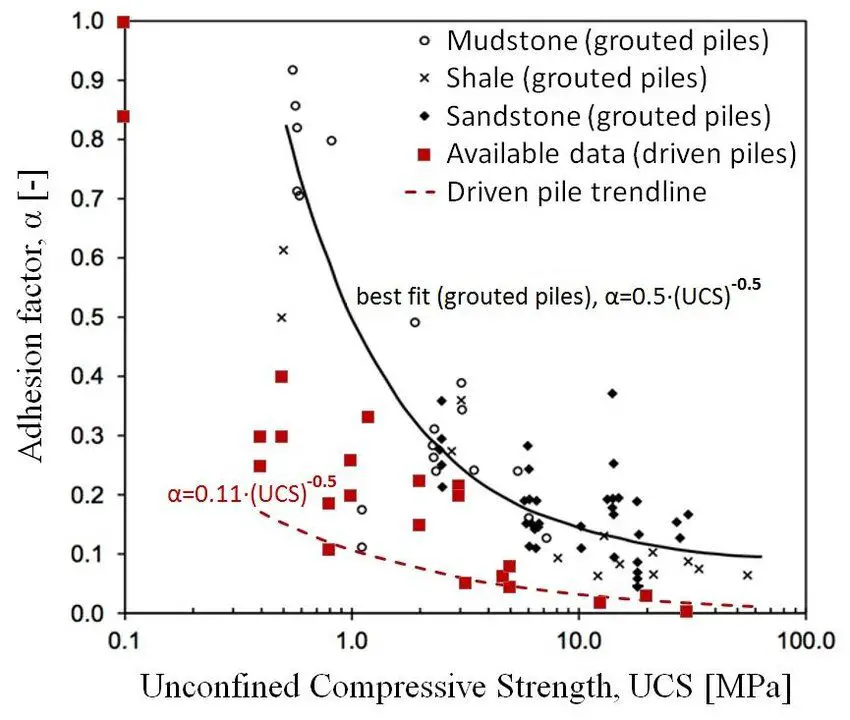
Cohesive soil or weak rock (mudstone)
q_s,k = αC_u —— (15)
q_b,k = C_uN_c —— (16)

Adhesion factor (α) can be read from chart, or determined from the unconfined compression test result (UCS). For piles in clay, N_cis usually taken as 9.0.

Undrained shear strength versus for a bored and b driven piles adapted from — **Figure 5***: Relationship between adhesion factor and undrained conhesion of soil*

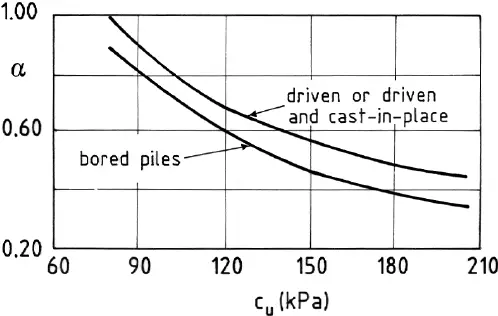
It is usually recommended that Cu < 40 kPa, α should be taken as 1.0.

AD FACTOR — Figure 5: Relationship between adhesion factor and unconfined compressive strength of soil

Design of pile foundation using static pile load test

The procedure for determining the compressive resistance of a pile from static load tests is based on analysing the compressive resistance, R_c,m, values measured in static load tests on one or several trial piles. The trial piles must be of the same type as the piles of the foundation, and must be founded in the same stratum.

An important requirement stated in Eurocode 7 is that the interpretation of the results of the pile load tests must take into account the variability of the ground over the site and the variability due to deviation from the normal method of pile installation. In other words, there must be a careful examination of the results of the ground investigation and of the pile load test results. The results of the pile load tests might lead, for example, to different ‘homogeneous’ parts of the site being identified, each with its own particular characteristic pile compressive resistance.

To use static load test result to design pile foundation, determine the characteristic value R_c,k from the measured ground resistance R_c,m using the following equation:

R_c,k = Min{(R_c,m)_mean/ξ₁; (R_c,m)_min/ξ₂} —— (17)

where ξ₁ and ξ₂ are correlation factors related to the number n of piles tested, and are applied to the mean (R_c,m)_mean and to the lowest (R_c,m)_min of R_c,m, respectively. The recommended values for these correlation factors, given in Annex A, are intended primarily to cover the variability of the ground conditions over the site. However, they may also cover some variability due to the effects of pile installation.

correlation factors for static pile load test 1

The design pile compressive resistance, R_c,d is obtained by applying the partial factor γt to the total characteristic resistance or the partial factors γs and γb to the characteristic shaft resistance and characteristic base resistance, respectively, in accordance with the following equations:

R_c,d = R_c,k/γ_t —— (18)
or
R_c,d = R_b,k/γ_b + R_s,k/γ_s —— (19)

R_c,d for persistent and transient situations may be obtained from the results of pile load tests using DA-1 and DA-2 and the recommended values for the partial factors γ_t or γ_s and γ_b given in Tables A.6, A.7 and A.8 of EN 1997-1:2004.

Question of the day | 18-12-2020

By

Ubani Obinna

-

December 18, 2020

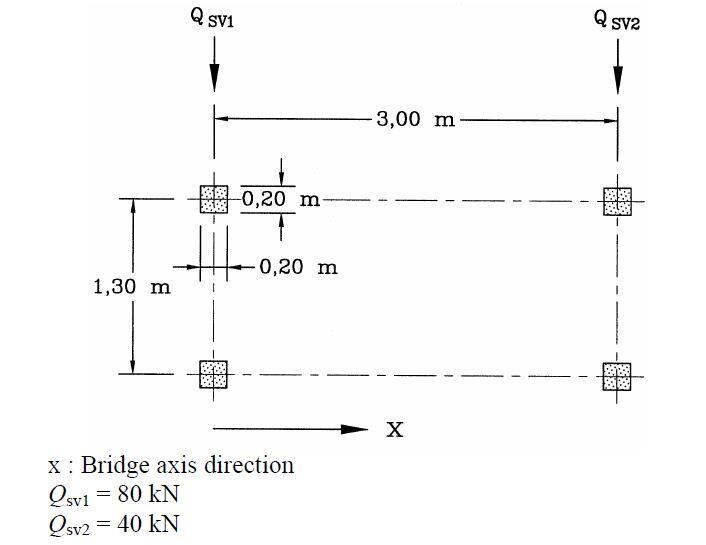
For the structure loaded as shown above;

(1) What is the bending moment at point B? (take clockwise moment as negative).

(A) -4 kNm
(B) -2.25 kNm
(C) -8 kNm
(D) -2 kNm

(2) What is the bending moment at support A? (take clockwise moment as negative)

(A) -4 kNm
(B) -2.25 kNm
(C) -8 kNm
(D) -2 kNm

Unit Weight of Construction Materials

By

Ubani Obinna

-

December 17, 2020

Table of Contents

Unit weight or density is used to quantify the weight per unit volume of an object. When it is expressed in the basic SI Unit of mass (kg/m³), it is usually referred to as density, but when expressed in terms of weight (kN/m³), it is usually referred to as unit weight.

Density (kg/m³) = Mass (kg)/Volume (m³)

The unit weight of a material is very important in calculating the self-weight of the material, especially when evaluating the permanent actions in a structure. Without the knowledge of the unit weight of a material, it will be impossible to accurately estimate the bodyweight and the load it subsequently carries when used as a structural member. This article is dedicated to providing a handy list of the unit weight of various construction materials according to EN 1991-1-1:2002.

The density of a material can vary depending on the composition, process of manufacturing, and other factors. However, the density of man-made products is fairly constant (or controllable) when compared with the density of direct products of nature. Therefore, natural materials are expected to have slightly different properties even when they are occurring in the same place.

(a) Unit weight of concrete and mortar

Materials	Density (kN/m³)
Hardened normal weight concrete	24.0
Reinforced concrete (normal percentage)	25.0
Fresh concrete	25.0
Cement mortar	19.0 to 23.0
Gypsum mortar	12.0 to 18.0
Lime-cement mortar	18.0 to 20.0
Lime mortar	12.0 to 18.0

(b) Unit weight of natural stones

Natural Stone	Unit weight (kN/m³)
granite, syenite, porphyry	27.0 to 30.0
basalt, diorite, gabbro	27.0 to 31.0
tachylyte	26.0
basaltic lava	24.0
gray wacke, sandstone	21.0 – 27.0
Dense limestone	20.0 – 29.0
other limestone	20.0
volcanic tuff	20.0
gneiss	30.0
slate	28.0

(c) Unit weight of timber and timber derived products

Timber/timber derived product	Unit weight (kN/m³)
timber strength class C14	3.5
timber strength class C22	4.1
timber strength class C30	4.6
timber strength class D30	6.4
timber strength class D50	7.8
timber strength class D70	10.8
homogeneous glulam GL24h	3.7
homogeneous glulam GL32h	4.2
combined glulam GL24c	3.5
combined glulam GL32c	4.0
combined glulam GL36c	4.2
softwood plywood	5.0
birch plywood	7.0
laminboard and blockboard	4.5
chipboard	7.0 to 8.0
cement-bonded particle board	12.0
flake board, oriented strand board, wafer board	7.0
hardboard, standard and tempered	10.0
medium density fibreboard	8.0
softboard	4.0

(d) Unit weight of metals

Metal	Unit weight (kN/m³)
aluminium	27.0
brass	83.0 – 85.0
bronze	83.0 – 85.0
copper	87.0 – 89.0
cast iron	71.0 – 72.5
wrought iron	76.0
lead	112.0 – 114.0
steel	77.0 – 78.5
zinc	71.0 – 72.0

(e) Unit weight of glass and plastics

Material	Unit weight (kN/m³)

Broken glass	22.0
Glass in sheets	25
Acrylic sheet – plastic	12.0
polystyrene, expanded, granules	0.3
foam glass	1.4
Terracota (solid)	21
Cork (compressed)	4

(f) Unit weight of asphalt/pavement materials

Material	Unit weight (kN/m³)
gussasphalt and asphaltic concrete	24.0 – 25.0
mastic asphalt	18.0 – 22.0
hot rolled asphalt	23.0
sand (dry)	15.0 – 16.0
hardcore	18.5 – 19.5
Quarry dust	14.1

(g) Roofs and roofing materials

Material	Weight per unit area (kN/m²)
Steel roof trusses in spans up to 25 m	1.0 – 2.0
Corrugated asbestos-cement or steel sheeting, steel purlins etc.	0.4 – 0.5
Roofing felt and screed	2.0
Patent glazing (with lead-covered astragals), steel purlins etc.	0.4
Slates or tiles, battens, steel purlins etc.	0.7 – 0.9
Plain roofing tiles	0.6 – 0.9
Interlocking roofing tiles	0.6
0.45 mm gauge aluminium roofing sheet	0.014

(h) Block works, brick works, partitions, and wall finishes

Material	Weight per unit area (kN/m²)
225 mm block work	2.87
150 mm sandcrete block work	2.15
Wall finishes (both sides)	0.6
12 mm plaster rendering	0.3
Two-coat gypsum 12 mm thick	0.215
Plasterboard 13 mm thick	1.1
Gypsum panels 75 mm thick	4.4
Clay hollow block	0.0113 / mm thick
Common clay blocks	0.0189 / mm thick
Engineering clay bricks	0.0226 / mm thick
Refractory bricks	0.0113 / mm thick

(i) Floor finishes

Material	Weight per unit area (kN/m²)
Clay floor tiles	0.575
25 mm thick terrazo floor	0.6
37 mm thick screeding	0.8
Terrazo paving	0.0222 / mm thick
6 mm thick glazed tile + adhesive	0.181
8 mm thick glazed tile + adhesive	0.214
10 mm thick glazed tile + adhesive	0.246
10 mm thick porcelain floor tiles + adhesive	0.275
8 – 10 mm thick vitrified floor tiles + adhesive	0.215
10 mm thick granite floor tiles + adhesive	0.346
12 mm thick granite floor tiles + adhesive	0.4
20 mm thick granite floor tiles + adhesive	0.622

Loads on Footbridges | Actions on Pedestrian Bridges

By

Ubani Obinna

-

December 16, 2020

Table of Contents

A footbridge (also called a pedestrian bridge) is a structure that is designed to enable pedestrians to cross over natural or man-made obstacles such as busy highways, railways, water bodies, gullies, etc, with minimal risk. Pedestrians are generally humans that are travelling on foot and also includes people in a wheelchair, or people that are pushing tramps. In the design of a footbridge, it is very important to evaluate the loads (actions) that it will encounter during its service life.

The possible loads that footbridges are subjected to are;

Human traffic
Self-weight of the bridge and its ancillaries
Wind load
Earthquake load (where applicable)
Snow load (where applicable)
Dynamic water pressure (for bridges crossing water bodies)
Thermal actions
Possible accidental action from impact

In the recent wake of the need for sustainable urban transportation, some pedestrian bridges are being designed to accommodate both pedestrians and cyclists. Furthermore, to ensure that footbridges are accessible to the disabled and mobility-impaired people, there should be provision for ramps or lifts so that they can cross over safely. The use of lifts should be a better option compared to ramps due to the high demand for space, especially in urban areas.

Pedestrian bridges can also serve as monumental structures that can be used for the decoration and beautification of cities and streets. Beautiful and well designed footbridges can adorn the skylines of a city, and form unique features that can easily attract tourists.

Bridge In Vietnam Hands — **Figure 1**: The Golden Bridge in Vietnam – A famous pedestrian bridge that opened in 2018

Actions on Footbridges

The actions on pedestrian bridges can be found in section 5 of EN 1991-2 (Eurocode 1 Part 2). The section covers explicitly actions on footways, cycle tracks, and footbridges. It is important to note that the uniformly distributed load q_fk and the concentrated load Q_fwk given in section 5 of EN 1991-2, where relevant can be also used for parts of road and railway bridges accessible to pedestrians. However, all other variable actions described therein apply to footbridges only.

Furthermore, it is important to note that the load models and their representative values take into account dynamic amplification effects, and can be used for all kind of serviceability and ultimate limit state static calculations, except fatigue limit states. The load models do not cover the effects of loads on construction sites and should be separately specified, where relevant.

The imposed loads defined in EN 1991-2 result from pedestrian and cycle traffic, minor common construction and maintenance loads (e.g. service vehicles), and accidental situations. These loads give rise to vertical and horizontal, static, and dynamic forces.

Static Models for Vertical Loads on Footbridges

Three mutually exclusive vertical load models can be envisaged for footbridges. They are;

a uniformly distributed load representing the static effects of a dense crowd;
one concentrated load, representing the effect of a maintenance load;
one or more, mutually exclusive, standard vehicles, to be taken into account when maintenance or emergency vehicles are expected to cross the footbridge itself.

crowd loads on footbridges in Lagos — **Figure 2:** Crowd on a pedestrian bridge, at Ojota Lagos, Nigeria

The characteristic values of these load models should be used for both persistent and transient design situations.

Uniformly Distributed Loads on Footbridges

The crowd effect on the bridge is represented by a uniformly distributed load. When the risk of dense crowd exists or when specified for a particular project, Load Model 4 for road bridges should be considered also for footbridges. On the contrary, where the application of the aforesaid Load Model 4 is not required, a uniformly distributed load, to be applied to the unfavourable parts of the influence surface longitudinally and transversally, q_fk should be defined in the National Annex.
The recommended value, depending on the loaded length L [m] is:

2.5 kN/m² ≤ q_fk = 2 + 120/(L + 30) ≤ 5.0 kN/m² —— (1)

For road bridges supporting footways or cycle tracks, only the characteristic values (5 kN/m²) or the combination value (2.5 kN/m²) should be considered.

pedestrian load on a bridge — **Figure 3:** Characteristic load on a footway (or cycle track) of a road bridge

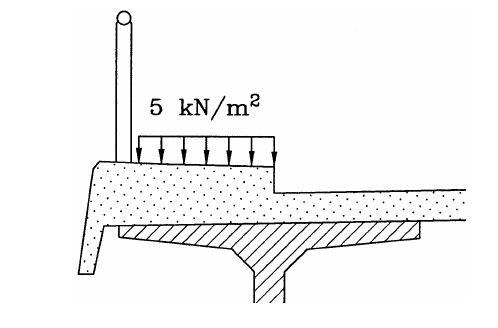
The minimum and maximum crowd load to be applied on bridges irrespective of the span length is therefore 2.5 kN/m² and 5 kN/m² respectively. To check the effect of span length on the value of the crowd load, equation (1) can be used. For instance, the crowd load on a pedestrian bridge of length 30 m is given by;

q_fk = 2 + 120/(L + 30) = 2 + 120/(30 + 30) = 4 kN/m²

Concentrated load on Footbridges

For local effect assessment, a 10 kN concentrated load Q_fwk, representing a maintenance load, should be considered on the bridge, acting on a square surface of sides 10 cm. When the service vehicle (see paragraph below) is taken into account, Q_fwk should be disregarded. The concentrated load Q_fwk should not be combined with any other variable non-traffic load.

Service/Accidental vehicle on Footbridges

When service vehicles for maintenance, emergencies (e.g. ambulance, fire), or other services must be considered, they should be assigned for the particular project. If no information is available and if no permanent obstacle prevents a vehicle from being driven onto the bridge deck, the special vehicle defined in the figure below should be considered. If consideration of the service vehicle is not requested, the vehicle shown in the figure below should be considered as accidental.

service or accidental vehicles on footbridges — **Figure 4**: Service or accidental vehicles on footbridges

Horizontal forces – characteristic values

A horizontal force Q_flk acting along the bridge deck axis at the pavement level should be taken into account for footbridges only, whose characteristic value is equal to the greater of these two values:

– 10 per cent of the total load corresponding to the uniformly distributed load or
– 60 per cent of the total weight of the service vehicle, when relevant.

This horizontal force, which is normally sufficient to ensure the horizontal longitudinal stability of the footbridge, is assumed to act simultaneously with the corresponding vertical load, and in no case with the concentrated load Q_fwk.

Groups of traffic loads on footbridges

Vertical loads and horizontal forces due to traffic should be combined, when relevant, taking into account the groups of loads defined in the table below (Table 5.1, EN 1991-2). Each of these groups of loads, which are mutually exclusive, should be considered as defining a characteristic action for combination with non – traffic loads.

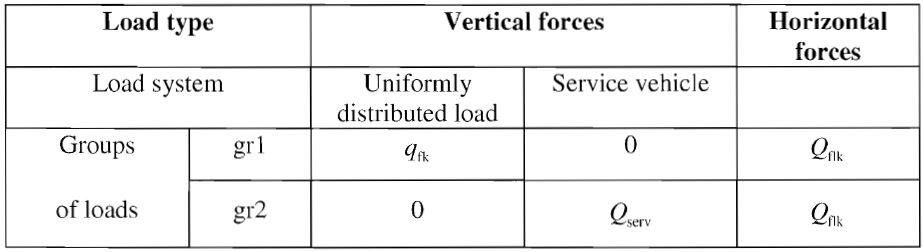
As a rule, except for roofed bridges, where appropriate rules are defined in EN 1991-1-3, traffic loads on footbridges are considered not to act simultaneously with significant wind or snow. Wind and thermal actions should not be taken into account as simultaneous. When a combination of traffic loads together with actions specified in other Parts of EN 1991 must be considered, any group of loads in Table 5.1 of EN 1991-2 should be considered as one action.

Application of the load models

The traffic models described above with the exception of the service vehicle model, may also be used for pedestrian and cycle traffic on the areas of the deck of road bridges limited by parapets and not included in the carriageway, or on the footpaths of railway bridges. These actions are free, so that the models of vertical loads should be applied anywhere within the relevant areas in such a way that the most adverse effect is obtained.

Design of a Building Against Internal Explosion

By

Ubani Obinna

-

December 15, 2020

According to section 5 of EN 1991-1-7:2006 (Eurocode 1 Part 7), explosions shall be taken into account in the design of buildings or civil engineering structures where gas is burned or regulated. This requirement also extends to buildings where materials such as explosive gases, or liquids forming explosive vapour or gas are stored or transported (e.g. chemical facilities, vessels, bunkers, sewage constructions, dwellings with gas installations, energy ducts, road and rail tunnels).

Explosion pressures on structural members should be determined taking into account, as appropriate, reactions transmitted to the structural members by non-structural members. The basic principle for design is that the structure shall be designed to resist progressive collapse resulting from an internal explosion, in accordance with EN 1990, 2.1 (4)P. In the design, the failure of some parts of the building may be permitted, but not the key structural members such as columns, slabs, beams, shear walls, etc.

Internal Gas Explosion in a Building

A gas explosion can be defined as a process where the combustion of a premixed gas-air cloud causes a rapid increase of pressure. For the proper functioning of a building, gas is required to supply energy for heating, cooking, and electricity generation. This implies the potential for an accidental explosion. For a gas explosion to occur in a building, the following succession of circumstances is required;

A gas leakage or release occurs as a result of technical defects in gas installations (pipes, boilers, etc.), human errors during installation, repair, or maintenance of such installations, or in consequence of intentional manipulation.
The released gas forms, with the oxygen present in the air, an inflammable gas-air cloud in compliance with certain physical requirements.
A delayed ignition of the gas-air mixture through an ignition source (spark, hot surface, etc) occurs. If the ignition takes place immediately after the gas release, i.e. before an inflammable gas-oxygen cloud is being formed, a fire might occur, but the mixture will not explode.

gas explosion destroys part of a building in Russia — **Figure 1**: Gas explosion destroys part of a building in Russia

The pressure build-up during a gas explosion in the inside of a building is a consequence of combustion in a confined environment. The combustion process results in increased temperatures due to the transformation of chemically bound energy into heat. Thereby, the expansion of the combustion products, such as CO₂ and vapour, will be limited due to confinement by the building closings such as walls and floors, which will cause the pressure to increase [1].

In a completely confined compartment, such as pipes or closed vessels in industrial installations, the maximum pressure generated during a gas explosion will depend primarily on the burning velocity (velocity of the flame front relative to the unburned gas immediately ahead of the flame). This velocity depends on the composition of the inflammable gas cloud, i.e. the gas type and the proportions of gas and air [1].

The highest pressures will arise if these proportions are such that there is no excess of fuel nor oxygen after the chemical reaction has been completed, what is referred to as the stoichiometric composition. For methane gas, for instance, which is the principal constituent of natural gas, the highest explosion pressures will arise for gas concentrations of about 10%. Below a methane gas concentration of 4%, and above 17%, no explosion will occur [1].

These so-called lower and upper flammability limits depend on the type of gas involved, the initial pressure (p₀), and temperature (t₀). The mentioned values for methane gas correspond to ambient conditions (t₀ = 20º, p₀ = 1 bar).

Simulated internal explosion pressure generation in a building — **Figure 2**: Simulated explosion pressure generation in a cubical, vented compartment [1]

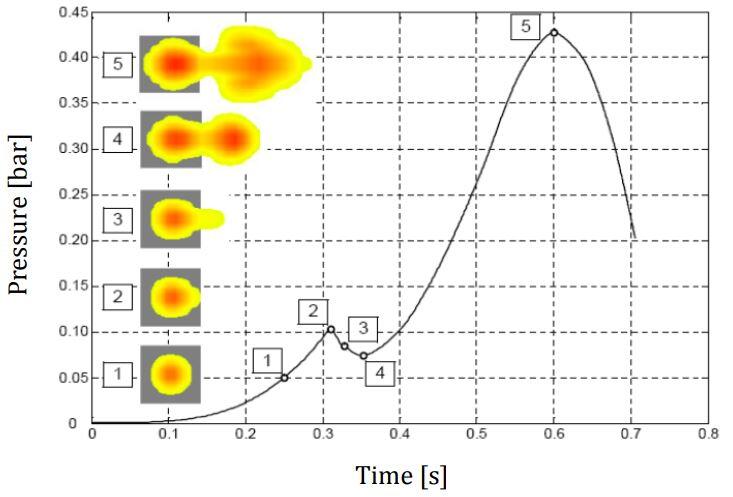
The ignition of a hydrocarbon gas-air cloud in a fully confined compartment might entail explosion pressures up to approximately 8 bars (800 kN/m²). Gas explosion in buildings, however, do not cause pressures of this magnitude. The main reasons are imperfect mixing of the gas-air cloud and the fact that these explosions are only partly confined. Windows, doors, light partition walls, or unrestrained brick walls act as venting elements, which, in case of failure provide explosion pressure relief. The table below culled from [1] gives typical failure pressures of these elements.

Element	Typical failure pressure (kN/m²)
Glass windows	2 – 7
Room doors	2 – 3
Light partition walls	2 – 5
Breeze block walls (50 mm)	4 – 5
Unrestrained brick walls	7 – 15

According to [2], key structural elements in a building should be designed to withstand the effects of an internal natural gas explosion, using a nominal equivalent static pressure, given by:

p_d = 3 + p_stat —— (1)
or
p_d = 3 + 0.5p_stat + 0.04/(A_v/V)² —— (2)

Whichever is greater.

Where;
p_stat = uniformly distributed static pressure in kN/m² at which venting components will fail,
A_v is the area of venting components, and
V is the volume of the room.

This equation is found in Annex D of BS EN 1991-1-7:2004.

The venting components represent here the non-structural part of the enclosure (e.g. wall, floor, ceiling) with limited resistance that is intended to relieve the developing pressure from deflagration in order to reduce pressure on structural parts of the building. The explosive pressure acts effectively simultaneously on all of the bounding surfaces of the room. The expressions are valid for rooms up to a volume of 1000 m³ and venting areas over volume ratios of 0.05 m^-1 ≤ A_v/V ≤ 0.15 m^-1.

An important issue is further raised in Clause 5.2 of EN 1991-1-7 [2]. It states that the peak pressures in the main text may be considered as having a load duration of 0.2 s. The point is that in reality, the peak will generally be larger, but the duration is shorter. So combining the loads from the above equations with a duration of 0.2 s seems to be a reasonable approximation.

For purpose of member design in the context of accidental actions, the Eurocode offers the following specific expression of the general formulation for design load combinations:

E_d = E(∑_j≥1 G_k,j + P + A_d + (ψ_1,1or ψ_2,1) ∙ Q_k,1 + ∑_i≥1 Ψ_2,i ∙ Q_k,i) —— (3)

Where:
G_k: Characteristic value of a permanent action
P: Representative value of a prestressing action
A_d: Design value of an accidental action
Q_k: Characteristic value of a variable action
ψ_1,1: Factor for the frequent value of a variable action
ψ_2,1: Factor for the quasi-permanent value of a variable action

It should be noted that in comparison to the corresponding expression for persistent- or transient design situations no partial safety factors are to be applied to load effects within the accidental load combination. The design value of the accidental action is directly defined by means of a value A_d, which in practice often corresponds to a nominal value, such as in the case of gas explosions, where A_d is represented by a nominal, static equivalent pressure.

The reason for the use of nominal values is that a reliable statistical characterization of both occurrence and magnitude of accidental actions can only seldom be carried out because the available data is generally poor.

A Design Example of a Building for an Internal Explosion

Let us consider a kitchen on the first floor of a block of flats in Port Harcourt. The floor dimensions of the kitchen are 3 x 4 m while the storey height is 3m. The kitchen is characterised by a significant window and door opening of area 5 m² (we are going to treat this as the venting area). Let us treat other walls in the kitchen as load-bearing.

This means that the volume V and the area of venting components A_v for this case are given by:

A_v = 5 m²
V = 3 × 4 × 3 = 36 m³

So the parameter A_v/V can be calculated as:

A_v/V = 5/36 = 0.138 m^-1

As V is less than 1000 m³ and A_v/V is well within the limits of 0.05 m^-1 and 0.15 m^-1 it is allowed to use the loads given in the code. The collapse pressure of the venting panels p_stat is estimated as 4 kN/m².

The equivalent static pressure for the internal natural gas explosion is given by:

p_Ed = 3 + p_stat = 3 + 4 = 7 kN/m²
or
p_Ed = 3 + p_stat/2 + 0.04/(A_v/V)² = 3 + (4/2) + 0.04/(0.138)² = 7.1 kN/m²

Therefore, the design pressure should be taken as the highest, which in this case is 7.1 kN/m²

According to Eurocode EN 1990 (Basis of design), these pressures have to be combined with the self-weight of the structure and the quasi-permanent values of the variables loads. Let us consider the design consequences for the various structural elements.

Bottom floor
Let us start with the bottom floor of the kitchen. Let the self-weight of the floor and finishes be 4.95 kN/m² and the imposed load 2 kN/m² (ψ₁ = 0.5 for considered category A). This means that the design load for the explosion is given by:

p_Ed = g_k + A_d + ψ₁q_k = 4.95 + 7.1 + 0.5(2) = 13.05 kN/m²

The design for normal conditions is given by:
p_Ed = γ_Gg_k + γ_Qq_k = 1.35(4.95) + 1.5(2) = 9.68 kN/m²

According to [2], we should keep in mind that for accidental actions there is no need to use a partial factor on the resistance side. So for comparison, we could increase the design load for normal conditions by a factor of 1.2. The result could be conceived as the resistance of the structure against accidental actions, if it designed for normal loads only. Hence,

p_Rd = 1.2 x 9.68 = 11.616 kN/m²

Dynamic Increase in Load Bearing Capacity
It is now time to remember the clause in Annex B of Eurocode EN 1991-1-7. If we take into account the increase in short duration of the load we may increase the load-bearing capacity by a factor φ_d given by:

φ_d = 1 + √(g_k/p_Rd) x √(2u_max/g∆_t²) —— (4)

Where;
g_k = 4.95 kN/m²
p_Rd = 11.616 kN/m²
g = acceleration due to gravity = 9.81 m/s²
u_max = 0.2 m (midspan deflection at collapse)
∆_t = 0.2 seconds

φ_d = 1 + √(4.95/11.616) x √[(2 x 0.2)/(9.81 x 0.2²)] = 1.652

p_REd= φ_d p_Rd = 1.652 x 11.616 = 19.189 kN/m² > 13.05 kN/m²

Therefore under the design condition, the bottom slab can be said to be fulfilling the design requirements.

Upper floor
Let us next consider the upper floor. Note that the upper floor for one explosion could be the bottom floor for the next one. The design load for the explosion, in that case, is given by (upward value positive!):

p_Ed = g_k + A_d + ψ₁q_k = = – 4.95 + 7.1 + 0 = 2.15 kN/m²

So the load is small, but will give larger problems anyway. The point is that the load is in the opposite direction of the normal dead and live load. This means that the normal resistance may simply be close to zero. What we need is top reinforcement in the field and bottom reinforcement above the supports. So it will be normal to reinforce the floor slab top and bottom.

An important additional point to consider is the reaction force at the support. Note that the floor could be lifted from its supports, especially in the upper two stories of the building where the normal forces in the walls are small. In this respect, edge walls are even more vulnerable. The uplifting may change the static system for one thing and lead to different load effects, but it may also lead to freestanding walls. If the floor to wall connection can resist the lift force, one should make sure that the also the wall itself is designed for it.

Design of the walls/columns
Depending on the support condition of the walls/columns, the design pressure should be applied as a lateral load to the columns/walls, and the maximum bending moment determined. This should be combined with the axial force in the column/wall to determine the appropriate reinforcement.

References
[1] Hingorani R. (2017): Acceptable life safety risks associated with the effects of gas explosions on reinforced concrete structures. PhD thesis submitted to the Department of Civil Engineering, UNIVERSIDAD POLITÉCNICA DE MADRID
[2] Vrouwenvelder T., Diamantidid D. (2009): Accidental Actions (Chapter 5) in Load Effects on Buildings (Milan Hilicky et al Eds). CTU in Prague, Klokner Institute

The 2018 Earthquake Induced Flow-Slide in Jono Oge Sulawesi, Indonesia

By

Ubani Obinna

-

December 12, 2020

On September 28, 2018, a large earthquake of magnitude (Mw) 7.5 struck Sulawesi Island, Indonesia. A major cause of large fatalities from this event (more than 1,300 people missing who may be still buried under the mudflows) was large-scale mass movements of soil at Petobo, Balaroa, and Jono Oge regions [1]. Generally, the capital city of Palu of Central Sulawesi Province was devastated by cascading geological hazards – strong shaking due to the mainshock, triggered tsunamis, and large scale soil movement (flow-slide).

Sulawesi Island is located within a triple junction of the Australian, Philippine, and Sunda Plates, and is heavily affected by the complex interaction of their movements. The earthquake occurred along the Palu-Koro Fault, which is known to be active and is influenced by the complex tectonic interaction of major subducting plates. The Palu-Koro fault is said to accommodate a deformation of about 40 mm/year, and has caused several devastating earthquakes in the past [1, 2].

According to researchers from Japan and Indonesia [2], the provinces of Balaroa, Petobo, Jono-Oge and Sibalaya were the worst hit in the 2018 earthquake mainly due to large-scale flow-slides and mudflows. Never before have such large-scale flow failures been triggered by an earthquake. That these failures occurred on very gentle sloping ground, sweeping away localities along with it, came as a complete surprise to one and all. The flow-slide in Jono Oge was deemed the largest in the region.

OVERVIEW OF LONG DISTANCE FLOW SLIDE — **Figure 1**: Overview of long distance flow-slide [2]

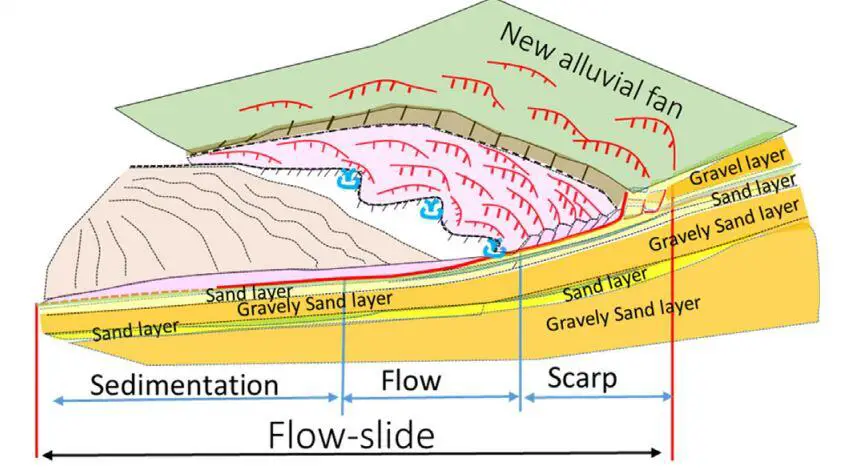
According to [2], the damaged area of long-distance flow-slide in Jono Oge is about 210 ha, located on the east side of Palu Valley, about 4 km south of Petobo. It is reported that a total of 500 houses were damaged. The catchment area of the affected area is estimated at 4 km². The flow-slide occurred at the bottom of the alluvial fan created at the valley mouth where the discharged water was not observed during the survey.

The combination of many factors such as liquefaction of the sandy layer and the formation of water film due to the existence of a less-permeable cap layer, the presence of a confined aquifer, and the geology of the area are thought to have led to the flow-slide. According to an eye witness report from a person living in the area, sand ejecta was seen during and after the earthquake. Evidence of sand ejecta which suggests liquefaction was also observed in the area after the earthquake [3].

According to the article, in Jono Oge, a survivor was shooting a video while being flowed, which is currently available on Youtube, (see link below).

Researchers from Japan and Indonesia [3] used a combination of satellite imagery, aerial imagery, field surveys including collecting soil samples from the sites and conducting in-situ testing using Portable Cone Penetrometer, to investigate the mechanism of massive flow-slides. The paper was published in Elsevier – Soils and Foundations.

From the research, it was concluded that all major flow-slides in the Palu valley occurred at locations where a new alluvial fan meets an old alluvial fan based on the geological features of the area.

Furthermore, the presence of low permeable layers (silt and clay) over loosely deposited sandy and sandy gravel layers suggests the complex mechanism of the long-distance flow-slide at Jono-Oge can be explained by the ‘interlayer water film theory’.

Previous researches have revealed that liquefaction at a site with sandwiched lithology results in the liquified soil being trapped below the low permeability cap layer. This creates a thin interlayer of water, referred to as a ‘‘water film‘. The resulting inhibition of excess pore water pressure dissipation and presence of the water-film reduces the residual shear strength of the sandy soil layer to below the initial static shear stress. Consequently, even on a very gentle slope, lateral flow takes place due to the action of gravitational force until equilibrium is achieved.

It is further assumed by the researchers that damage to the underlying artesian aquifer during the earthquake may also have contributed to the development of the water film and the liquefaction induced flow-slide in the layers with very low mobilized shear resistance. The researchers however admitted the mechanism of the long-distance flow-slide is not yet fully understood.

Disclaimer
Every piece of information provided in this article is from the open access research work of the authors/publishers cited. They are not owned by www.structville.com. Open access articles are under the CC BY-NC-ND license. See (http://creativecommons.org/licenses/by-nc-nd/4.0/) for information on open access articles.

References

[1] Goda K., Mori N., Yasuda T., Prasetyo A., Muhammad A. and Tsujio D. (2019): Cascading Geological Hazards and Risks of the 2018 Sulawesi Indonesia Earthquake and Sensitivity Analysis of Tsunami Inundation Simulations. Front. Earth Sci. 7:261. doi: https://doi.org/10.3389/feart.2019.0026

[2] Kiyota T., Furuichi H., Hidayat R. F., Tada N., Nawir H. (2020): Overview of long-distance flow-slide caused by the 2018 Sulawesi earthquake, Indonesia. Soils and Foundations, 60(3):722-735 https://doi.org/10.1016/j.sandf.2020.03.015

[3] Hazarika H., Rohit D., Pasha S. M. K., Maeda T., Masyhur I., Arsyad A., Nurdin S. (2020): Large distance flow-slide at Jono-Oge due to the 2018 Sulawesi Earthquake, Indonesia. Soils and Foundations, ISSN 0038-0806, https://doi.org/10.1016/j.sandf.2020.10.007

.

Analysis of Laterally Loaded Piles

By

Ubani Obinna

-

December 10, 2020

Piles are used for resisting vertical and lateral loads that are transmitted to the substructure of buildings. Structures such as tall chimneys, highrise buildings, towers, offshore structures, tall retaining structures, wharfs and jetties, etc are normally subjected to high lateral loads, which are subsequently transferred to the foundations supporting them as lateral shears. If the lateral loads are too high, inclined or batter piles can be used to aid vertical piles for lateral load resistance (Murthy, 2012). The analysis of laterally loaded piles to determine the ground deflection, bending moment, shears, load-carrying capacity, etc is therefore very important for the purpose of design.

batter piles in a marine structure — **Figure 1**: Inclined concrete piles in a marine facility

Numerous researchers have worked on the experimental and theoretical solution to the problem of laterally loaded piles. Reese et al (1974) and Matlock (1970) developed the concept of p-y curves for solving laterally loaded pile problems. The method is quite popular in the United States of America. However, the p-y curve method has been reported to not predict pile response properly (Kim et al. 2004, Anderson et al. 2003).

Model of laterally loaded piles — **Figure 2:** Model of laterally loaded pile: (a) elevation view; (b) as elastic line; (c) p-y curves, Reese (1997)

According to Basu et al (2008), the failure of p-y curves to predict pile response properly is not surprising because the p-y curves, which describe the resistive properties of soil as a function of pile deflection, used in the p-y analysis are developed empirically by back-fitting the results of numerical analysis to match the actual field pile-load test results. Thus, p-y curves developed for a particular site are not applicable to other sites. In order to obtain an accurate prediction of lateral pile response by the p-y method, p-y curves must be developed through pile load tests for every site – an uneconomical alternative.

The problem of laterally loaded piles is closely related to the problem of beam on elastic foundation. While a beam on an elastic foundation can be loaded at any point along its length, the external loads on a pile are likely to be on or above the ground surface.

Most of the numerical solutions for laterally loaded piles involves the concept of modulus of subgrade reaction. This is based on Winkler’s assumption that a soil medium may be approximated by a series of closely spaced independent elastic springs (Murthy, 2012). It has been shown that the error inherent in Winkler’s hypothesis is not significant. Therefore in laterally loaded piles, a series of non-linear springs can be used to represent the force-deformation characteristics of the soil.

The key to the solution of laterally loaded piles problem, therefore, lies in the determination of the modulus of subgrade reaction with respect to depth along the pile. The soil reaction p at any point along the pile length x may be expressed as;

p = -E_sy —— (1)

where y is the deflection at point x, and E_s is the soil modulus.

The relationship between the soil resistance per unit length (p) and deflection (y) is strongly non-linear. Therefore, E_s is not constant but changes with the deflection of the pile. There are many factors that influence the value of E_s such as the pile width, the flexural stiffness, the magnitude of the applied load, and the soil properties.

The variation of Es with depth for any prticular load level may be expressed as;

E_s = n_hx —— (2)

Where n_h is the coefficient of soil modulus variation. The variation of n_h with relative density D_r of sand is given in the Figure below;

variation of modulus of elasticity with relative density — **Figure 3:** Variation of n_h with relative density *D_r* (Reese, 1974)

Matlock and Reese (1960) provided a non-dimensional solution for the determination of deflection, slope, moment, shear, and soil reaction any point x along the pile. The equations are as follows;

Deflection (y) = [P_tT³/EI]A_y + [M_tT²/EI]B_y —— (3)
Slope (s) = [P_tT²/EI]A_s + [M_tT/EI]B_s —— (4)
Moment (M) = [P_tT]A_m + [M_t]B_m —— (5)
Shear (V) = [P_t]A_v + [M_t/T]B_v —— (6)
Soil reaction (p) = [P_t/T]A_p + [M_t/T²]B_p —— (7)

Where T is the relative stiffness factor expressed as;

T = [EI/n_h]^0.2 —— (8)

A and B are sets of non-dimensional coefficients that can be picked from Table (see Table 16.2, Murthy, 2012). The coefficients are given as functions of the depth coefficient Z expressed as;

Z = x/T —— (9)

For free headed piles at the ground level, the deflection and slope are as given below;

Deflection y_g = 2.43(P_tT³)/EI + 1.62(M_tT²/EI) —— (10)
Slope S_g = 1.62(P_tT²)/EI + 1.75(M_tT/EI) —— (11)

For fixed head piles;

y_g = 0.93(P_tT³)/EI —— (12)

The bending moment at ground level for fixed head is;

M_t = -0.93[P_tT] —— (13)

Brom’s Solution for Laterally Loaded Piles

Broms’ (1964a, 1964b) developed solutions for determining lateral deflections at ground level at working loads and ultimate lateral resistance of piles under lateral load using the concept of subgrade reaction. He developed solutions for long and short piles installed in cohesive and cohesionless soils in the form of charts.

Furthermore, laterally loaded piles are usually analysed depending on whether the head is free to rotate or fixed. The head of a pile may be considered as fixed when the stiff pile cap is tied using connecting beams.

Ultimate Lateral Resistance of Piles In Saturated Clays
The ultimate soil resistance of piles in cohesive soils increases with depth from 2c_u (c_u is the undrained shear strength) to 8 to 12c_u at a depth of 3 times the pile diameter (3d) from the ground surface. However, Broms suggested a constant value of 9c_u to be used as the ultimate soil resistance below a depth of 1.5d.

**Figure 5:** *Ultimate lateral load of short pile in cohesive soil (Broms, 1964a)*

Long pile in cohesive soil — **Figure 6:** *Ultimate lateral load of long pile in cohesive soil (Broms, 1964a)*

The solution for long piles involves the moment capacity of the pile section which should be calculated accordingly. A free-headed pile is considered long when βL > 2.5 and short when βL < 2.5. For a fixed-headed pile, a pile is long when βL > 1.5 and short when βL < 1.5.

β = (kd/4EI)^0.25 —— (14)

Where;
EI = stiffness of the pile
k = coefficient of horizontal subgrade reaction
d = width or diameter of pile
L = Length of pile

Ultimate Lateral Resistance of Piles in Cohesionless Soil
The ultimate lateral resistance of long and short piles embedded in cohesionless soils can be estimated from the chart below. For short piles, the dimensionless quantity P_u/γd³K_p is plotted against the L/d ratio while in long piles, P_u/γd³K_p is plotted against M_y/γd⁴K_p.

Where;
γ = the effective unit weight of the soil
K_p =Rankine’s passive earth pressure coefficient
M_y = Ulitimate moment capacity of the section

**Figure 7**: Ultimate lateral load of short pile in cohesionless soil (Broms, 1964b)

laterally long pile in cohesionless soil — **Figure 8:** *Ultimate lateral load of long pile in cohesionless soil (Broms, 1964b)*

Solved Example

A reinforced concrete square pile of dimensions 450 x 450 mm is driven to a depth of 20m in medium dense sand. The sand is in a saturated state. A lateral load of 250 kN is applied to the pile at 1 m at the ground level. Calculate the following;

(a) Lateral deflection of the pile at the ground level when the head is free (Use Matock and Reese Method)
(b) Lateral deflection of the pile at the ground level when the head is restrained (Use Matock and Reese Method)
(c) Ultimate lateral resistance of the pile (Using Brom’s method)

(n_h = 15000 kN/m²/m; f_cu = 40 N/mm²; A_sprov= 12Y20 (3768 mm²); φ = 35^o; M_u = 445 kNm; Submerged unit weight of soil = 8.75 kN/m³)

Solution
Ignoring the reinforcements, the flexural rigidity of the pile can be calculated;
f_cu = 40 N/mm²
E_c = 20 + 0.2f_cu = 20 + 0.2(40) = 28 kN/mm² = 2.8 × 10⁷ kN/m²
I = bh³/12 = (0.45 × 0.45³)/12 = 3.417 × 10^-3 m⁴

Hence;
E_cI = (2.8 × 10⁷) × (3.417 × 10^-3) = 95676 kNm²

T = (EI/n_h)^0.2 = (95676/15000)^0.2 = 1.448 m

(a) Lateral deflection at the ground when the head is free
Using Matlock and Reese method
y_g = 2.43(P_tT³)/EI + 1.62(M_tT³/EI)

P_t = 250 kN (given)
M_t = (250 × 1m) = 250 kNm

y_g = 2.43(250 × 1.448³)/95676 + 1.62(250 × 1.448²)/95676 = 0.0192 + 0.008875 = 0.028 m = 28 mm

Extra
Using Brom’s method;
η = (n_h/EI)^0.2 = (15000/95676)^0.2 = 0.69
ηL = 0.69 × 20 = 13.8

chart for lateral deflection — Figure 9: Chart for deflection of laterally loaded piles in coheiosnless soild (Broms, 1964b)

Reading from chart for ηL = 13.8; e/L = 1/20 = 0.05
[y_g(EI)^3/5(n_h)^2/5]/P_tL = 0.2

Therefore y_g = 0.2P_tL/(EI)^3/5(n_h)^2/5 = (0.2 × 250 × 20)/(95676^3/5 × 15000^2/5) = 0.0219 mm = 21.9 mm

When analysed on Staad Pro, a lateral deflection of 24.07 mm was obtained as shown in Figure 10;

staad pro model — **Figure 10**: Staad Pro numerical modelling results

(b) Lateral deflection when the head is restrained
Using Matlock and Reece method
y_g = 0.93(P_tT³)/EI = 0.93(250 × 1.448³)/95676 = 0.007377 = 7.38 mm

Extra
Using Brom’s method;
[y_g(EI)^3/5(n_h)^2/5]/P_tL = 0 (when the head is restrained)
Hence the lateral deflection can be taken as zero.

(c) Lateral load resistance of the pile
Coefficient of pasive pressure K_p = (1 + sinφ)/(1 – sinφ) = (1 + sin35)/(1 – sin35) = 3.69
Ultimate moment of resistance of section = 445 kNm
γ = 8.75 kN/m³
d = 0.45 m

Hence, the non-dimensional yield moment = M/γd⁴K_p = 445/(8.75 × 0.45⁴ × 3.69) = 336
For e/d = 1000/450 = 2.22

Reading from chart;
P_u/γd³K_p = 60 (for free-head condition)
P_u/γd³K_p = 80 (for fixed head condition)

Therefore,
P_u,free = 70γd³K_p = 60 × 8.75 × 0.45³ × 3.69 = 176.5 kN
P_u,fixed = 70γd³K_p = 80 × 8.75 × 0.45³ × 3.69 = 235 kN

Therefore, the pile section provided is inadequate for the service lateral load coming to the substructure. The pile section will have to be changed.

References
Anderson, J. B., Townsend, F. C. & Grajales, B. (2003): Case history evaluation of laterally loaded piles. J. Geotech. Geoenv. Engng., Am. Soc. Civ. Engrs. 129, No. 3, 187-196.

Basu D., Salgado R., Prezzi M. (2008): Analysis of Laterally Loaded Piles in Multilayered Soil Deposits. Publication FHWA/IN/JTRP-2007/23. Joint Transportation Research Program, Indiana Department of Transportation and Purdue University, West Lafayette, Indiana, 2008. doi: 10.5703/1288284313454

Broms B.B. (1964a): Lateral Resistance of Piles in Cohesive Soils. Journal of the Soil Mechanics and Foundations Division, 1964, Vol. 90, Issue 2, 27-6

Broms B.B. (1964b): Lateral Resistance of Piles in Cohesionless Soils. Journal of the Soil Mechanics and Foundations Division, 1964, Vol. 90, Issue 3, 123-156

Kim, T. K., Kim, N-K, Lee, W. J. & Kim, Y. S. (2004). Experimental load-transfer curves of laterally loaded piles in Nak-Dong river sand. J. Geotech. Geoenv. Engng., Am. Soc. Civ. Engrs. 130, No. 4, 416-425.

Matlock H. (1970): Correlations for Design of Laterally Loaded Piles in Soft Clay. Proceedings to the 2nd Offshore Technology Conference, Houston Texas, Vol 1

Murthy V.N.S. (2012): Soil Mechanics and Foundation Engineering. CBS Publishers and Distributors Pvt. Ltd, New Delhi, India

Reese, L.C. (1997): Analysis of laterally loaded piles in weak rock. J. Geotech. Geoenviron. Eng. 123 (11), 1010–1017

Reese, L.C., Cox, W.R., Koop, F.D.: Field testing and analysis of laterally loaded piles in stiff clay (1974): In Proceedings of the 6th Annual Offshore Technology Conference, pp. 672–690. Houston, Texas, 2(OTC 2312)

Design of Braced Cuts in Excavations

By

Ubani Obinna

-

December 9, 2020

In the construction of any substructure below the ground surface, excavations must be made to the recommended depth before the construction can begin. In the circumstances where deep vertical cuts (say about 3m) are to be made in a soil, provision must be made for the support of the soil to stop it from caving in or collapsing. The design of braced cuts involves the evaluation of the stresses in the members (bracings) used for supporting the cut, and provision of adequate members sizes or sections to avoid structural failure. These are usually classified as temporary works in construction.

Most shallow foundations in cohesive-frictional soils may not need side supports to keep the cut stable. Furthermore, when there is enough space, the sides of the excavation may be sloped, thereby eliminating the need for bracings or support. However, when a vertical excavation exceeds 3m depth, the most common practice is to drive vertical timber planks called sheeting along the sides of the excavation. Horizontal beams called wales are used to hold the sheeting in place, while struts running from side to side of the excavation is used to hold the wales in place.

For deeper cuts of about 5-6m, the use of timber sheeting may become uneconomical and steel sheet pile walls may be used (see figure below). Sheet piles are convenient to use because of their high resistance to stresses. On the other hand, they are relatively lightweight and reuseable when compared with timber.

design of braced cut for excavation — Typical construction of a braced cut using sheet pile walls

The sheet piles are driven around the boundary of the excavation. As the soil is removed from the enclosure, the wales and struts are inserted. The process continues until the excavation is complete. When the width of the excavation is too wide to permit the economical use of struts across the excavation, tiebacks may be used as shown below.

retaining wall tie back — Typical schematic representation of tieback

Lateral Earth Pressure Distribution in Braced Cuts

To design braced excavations (that is to select the wales, struts, sheet piles etc), the engineer must estimate the lateral pressure that the braced cut will be subjected to. The lateral earth pressure distribution of braced cuts is different from that of conventional retaining walls. This is because the deformation of braced cut walls gradually increases with the depth of the excavation. The deformation is influenced by factors such as type of soil, type of equipment used, depth of excavation, and workmanship.

Due to very little wall yielding at the top of the excavation, the pressure will be very close to at rest at the top. At the bottom of the wall with greater yielding, the lateral earth pressure will be lower than the Rankine active earth pressure. As a result of this, the earth pressure distribution of braced cuts varies significantly with that of retaining walls.

difference between the yielding of a retaining wall and a braced cut — Deformation behaviour of braced cuts and retaining walls

Peck in 1969 presented the pressure distribution diagram of braced cuts. The diagrams were developed from observations and studies obtained from the strut load of Berlin subway cut, Munich subway cut, and New York subway cut. He described the pressure as apparent pressure envelopes which represents the fictitious pressure distributions for estimating the strut loads in a braced cut.

pressure distribution diagram in cuts — Apparent pressure distribution in braced cuts

(a) For cuts in sand
The lateral pressure for cuts in sand is given by;

σ = 0.65γHK_a

Where;
γ = Soil unit weight
H = Height of the cut
K_a = Rankine’s active earth pressure

(b) For cuts in soft-medium clay (γH/c > 4)

The lateral pressure is the larger of;

σ = γH[1 – (4c/γH)] or σ = 0.3γH

(c) For cuts in stiff clay (γH/c ≤ 4)

σ = 0.2γH to 0.4γH (average of 0.3γH)

Where c is the undrained cohesion of the soil.

When using the pressure envelops in design, it is very important to keep the following in mind;

The pressure envelope is sometimes referred to as the apparent pressure envelope. The actual pressure distribution depends on the construction sequence and the flexibility of the wall.
The water table is below the bottom of the cut
Sand is assumed to be drained with no pore water pressure
Clay is assumed to be undrained, and pore water pressure is not considered
The excavation depth is greater than about 6 m

Design of the various components of a braced cut

Struts
Struts in braced cuts behave like horizontal columns. Hence, the load-carrying capacity depends on the slenderness ratio and flexural buckling capacity. During construction, it is recommended that struts should have a minimum vertical spacing of 3m. In clay soils, the depth of the first strut below the ground surface should be less than the depth of the tensile crack.

To determine the load in the strut, the following procedure can be used;

Draw the pressure envelope of the braced cut and show the strut levels. Assume that the sheet pile walls are hinged at the strut levels except for the top and bottom ones.
Determine the support reaction of the cantilever (for the top and bottom struts), and use simply supported assumption to determine the intermediate struts
Sum up the reactions to determine the load in each strut
Provide and appropriate section for the strut using a suitable design code

Sheet Piles
The following steps may be taken in the design of a sheet pile wall;

For each of the section (in plan), determine the maximum bending moment
Pick the highest value of the maximum bending moments (in kNm/m)
Obtain the required section modulus of the sheet pile wall S_x = M_max/Allowable stress of the sheet pile material
Choose a sheet pile section with a slightly higher section modulus

Wales
Wales may be treated as continuous horizontal members if they are properly spliced. Conservatively, they can be assumed to be pinned at the struts.

Design of Braced Cuts – Solved Example

A long trench is excavated in a medium dense sand for the basement of a highrise building. The excavation is supported with sheet pile walls held in place by struts and wales as shown in the figure below. The struts are spaced 4m c/c in plan.

Determine;

(a) The pressure envelope on the wall
(b) The loads in the struts
(c) The maximum moment for determining an appropriate section for the sheet piles
(d) The maximum moment for determining the section for the wales

Solution
(a) The pressure envelope on the wall
For a braced cut in sand, the apparent pressure envelope is given by;

σ = 0.65γHK_a
K_a = (1 – sin30)/(1 + sin 30) = 0.333
σ = 0.65 × 18 × 8.5 × 0.333 = 33.11 kN/m²

(b) Calculation of the strut load
Since the struts are spaced at 4m c/c in plan, the UDL = 33.11 × 4 = 132.44 kN/m

Section A – B
Taking moment about A;
3V_B1 – (33.11 × 3²)/2 + (33.11 × 1.5²)/2 = 0
V_B1 = 111.746/3 = 37.248 kN/m

Taking moment about B;
3V_A – (33.11 × 4.5²)/2 = 0
V_A = 335.238/3 = 111.746 kN/m

Section B – C
Taking moment about C;
3V_B2 – (33.11 × 3²)/2 + (33.11 × 1.0²)/2 = 0
V_B2 = 132.44/3 = 44.146 kN/m

Taking moment about B;
3V_C – (33.11 × 4²)/2 = 0
V_C = 264.88/3 = 88.293 kN/m

The shear force diagrams of the different sections are shown below;

In summary the strut loads are as follows;
V_A= 111.746 kN/m × 4m = 446.985 kN
V_B = V_B1 + V_B2= 37.248 kN/m + 44.146 kN/m = 81.394 kN/m × 4m = 325.576 kN
V_C = 88.293 kN/m × 4m = 353.173 kN

When the loads are factored, the struts can be designed as axially loaded steel columns.

(c) Bending moment on the sheet pile walls
By looking at the shear force diagram, we can confirm that the maximum moment will occur at the cantilever regions and at the points of contraflexure for shear.

For section A-B, the point of contraflexure of the shear force diagram can be obtained using similar triangle;

62.081 = (3 – x)
37.248 = x

On solving, x = 1.125 m from point B

Similarly for section B-C;

55.183 = (3 – x)
44.146 = x

On solving, x = 1.333 m from point B

Hence;
M_A = (33.11 × 1.5²)/2 = 37.25 kNm/m
M_C = (33.11 × 1.0²)/2 = 16.55 kNm/m
M_A-B,max = (37.248 × 1.125) – (33.11 × 1.125²)/2 = 20.951 kNm/m
M_B-C,max = (44.146 × 1.333) – (33.11 × 1.333²)/2 = 29.43 kNm/m

The maximum moment for the section is 37.25 kNm/m and should be used for the design of the sheet pile wall when factored.

(d) Design moment of the wales
We can use the maximum strut load to design the wale.

M_max= PL²/8

Where L is the spacing of the strut in plan
M_max = (111.746 x 4²)/8 = 223.492 kNm/m
The design can be carried out accordingly.

Special considerations should be given to braced cuts in layered soils (kindly refer to standard geotechnical engineering textbooks). Furthermore, heave at the bottom of braced cuts in clay soils should also be considered where applicable.

Column and slab systems

Rigid Frames

Shear wall-Frame Systems

Shear Truss-Outrigger Braced Systems

Framed-Tube System

Trussed Tube Systems

Bundled Tube Systems

Classification of Piles

Classification Based on Function or Action

Classification Based on Material and Composition

Classification Based on Method of Installation

Design of Pile Foundation

Approaches to the design of pile foundations

Pile Foundation Design to Eurocode 7

Static pile formulae based on ground parameters

Design of pile foundation using static pile load test

(a) Unit weight of concrete and mortar

(b) Unit weight of natural stones

(c) Unit weight of timber and timber derived products

(d) Unit weight of metals

(e) Unit weight of glass and plastics

(f) Unit weight of asphalt/pavement materials

(g) Roofs and roofing materials

(h) Block works, brick works, partitions, and wall finishes

(i) Floor finishes

Actions on Footbridges

Static Models for Vertical Loads on Footbridges

Uniformly Distributed Loads on Footbridges

Concentrated load on Footbridges

Service/Accidental vehicle on Footbridges

Horizontal forces – characteristic values

Groups of traffic loads on footbridges

Application of the load models

Internal Gas Explosion in a Building

A Design Example of a Building for an Internal Explosion

Brom’s Solution for Laterally Loaded Piles

Lateral Earth Pressure Distribution in Braced Cuts

Design of the various components of a braced cut

Design of Braced Cuts – Solved Example

EDITOR PICKS

POPULAR POSTS

POPULAR CATEGORY

ABOUT US

FOLLOW US