Drains are one of the components of the drainage system of residential areas and/or public infrastructures. Generically, roadside drains are structures used for collecting and conveying surface water to their discharge point, and in many cases, are artificial. Furthermore, drains are essential in road construction as stormwater ponding on pavement surfaces can cause premature pavement failure especially when unevaporated and undrained water seeps into the pavements.
The main objective of road drainage is to keep the road surface and foundation as dry as possible to maintain its stability. Thus, a good drainage system is essential for efficient highway transportation with minimum maintenance costs. Similarly, proper planning and design of road drainage systems are very important to prevent water from in-filtering the road surface, removing it from driving lanes, and carrying it away from the roadway.

Common Roadside Drain Cross-sections
The common cross-sections used for roadside drains construction are rectangular and trapezoidal sections. Trapezoidal drains have sloped sides and can be formed by excavating in-situ materials. The sloped sides and channel bottom may require paving for protection, depending on the stability of the sides and the resistance of the in-situ materials to erosion. However, trapezoidal drains are now formed with reinforced concrete, which may be precast units or cast-in-place.


Similarly, rectangular drains have vertical or near-vertical sides, formed with reinforced concrete retaining walls, I-walls, or U-frame structures. The bottom of the channel may be paved or unpaved depending on the resistance of the in situ material to erosion.
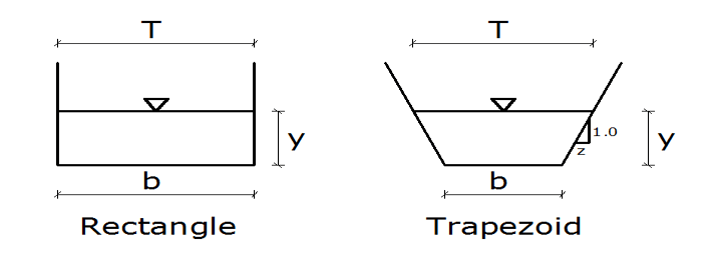
| Cross-section | Flow Area (A) | Wetted Perimeter (P) | Top width (T) | Hydraulic Radius (R) |
| Rectangular | by | b + 2y | b | A/P |
| Trapezoidal | y(b + yz) | b + 2y√(1 + z2) | b + 2yz | A/P |
Best Hydraulic Cross-section
The best cross-section for a drainage channel provides adequate hydraulic capacity at the minimum cost. Economic considerations for selecting the channel section include design and construction costs, right-of-way, required relocations, maintenance and operation.
A trapezoidal channel is usually the most economical channel when right-of-way is available. In contrast, a rectangular channel may be required for channels located in urban areas where the right-of-way is severely restricted or available at a high cost. Furthermore, site developments, existing geophysical site conditions, and performance or service requirements affect the selection of channel type and the resulting construction costs.
For discharge to be maximum or for the best hydraulic cross-section in a rectangular channel;
b = 2y and R = y/2
For trapezoidal channel;
T + 2yz = 2y√(z2 + 1)
R = y/2
A = 3(1/2) × y2
b = 2y/3(1/2)
Z = 1/3(1/2) = 0.577
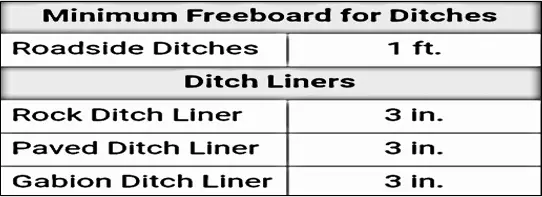
Freeboard for Drains
In open channels or drains, freeboard is of great importance. The provision of freeboard in open drains ensures enough room for wave action and flow surges not to overtopping or overflow the drain. Many uncontrolled causes may create wave action or water surface fluctuation, but mostly because of changes in specific energy of the flow in a channel.
Therefore, a freeboard is provided to ensure the drain is not filled with water. In addition, the calculated discharge rate does not consider deposited solids and lack of maintenance, which will usually reduce the system’s efficiency.
A table for minimum freeboard for ditches is provided below;
Worked Example
It was estimated from hydrological analysis that the peak discharge from a catchment area is 1.351m3/s. Using Manning’s equation, determine the best hydraulic cross-section for a rectangular and trapezoidal roadside drain. Other assumptions for computation are provided below.
Q = VA
V= 1/n x R2/3 × S1/2
Where:
Q = Discharge (m3/s)
A = Flow area (m2)
V = Allowable velocity (m/s)
R = Hydraulic radius (m)
Manning’s roughness coefficient (n) = 0.014
Bed slope of channel (S) = 3% (0.03)
Solution
From
Q = VA ——– (1)
Q = 1/n × R2/3 × S1/2 × A ——– (2)
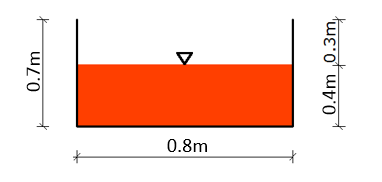
(a) For the best hydraulic section for the rectangular drain;
b = 2y and R = y/2
Cross-sectional area of drain (A) = by
Substituting b = 2y into the area formula;
Cross-sectional area of drain (A) = (2y)y = 2y2
Substituting Q, n, R, S and A into Equation (2);
1.351= 1/0.014 × (y/2)2/3 × 0.031/2 × 2y2
1.351= 1/0.014 × (y/2)2/3 × 0.1732 × 2y2
1.351= 1/0.014 × y2/3/1.5874 × 0.1732 × 2 × y2
y8/3 = 0.087m
y = 0.0873/8 = 0.4 m
Cross-sectional area of drain (A) = 2y2 = 2 × 0.42 = 0.32m2
Width of drain (b) = 2y = 2 × 0.4 = 0.8 m
It is necessary to provide freeboard of at least 1 ft (0.3 m)
Therefore, drain depth = 0.4 + 0.3 = 0.7 m
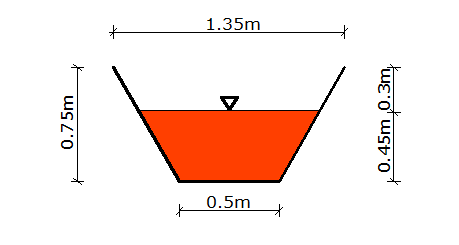
(b) For the best hydraulic section for the trapezoidal drain;
Area of drain (A) = 31/2 × y2
R = y/2
Bottom width (b) = 2y/31/2
Z = 1/31/2 = 0.577
Substituting Q, n, R, S and A into Equation (2)
1.351 = 1/0.014 × (y/2)2/3 × 0.031/2 × (31/2 × y2)
1.351 = 1/0.014 × (y/2)2/3 × 0.1732 × 1.7321 x y2
1.351 = 1/0.014 × y2/3/1.5874 × 0.1732 × 1.7321 x y2
y8/3 = 0.1 m
y = 0.0873/8 = 0.422 m (approximated to 0.45 m)
Cross-sectional area of drain (A) = 31/2 × y2 = 31/2 × 0.4222 = 0.308 m2
Depth of drain = 0.422 + 0.3 = 0.722 m (approximated to 0.75 m)
Bottom width of drain (b) = 2y/31/2 = 2 x 0.422/31/2 = 0.487 m (approximated to 0.5m)
Top width (T) = b + 2yz = 0.487 + (2 x 0.722 x 0.577) = 1.32 m (approximated to 1.35m)
Conclusion
The best hydraulic section of a roadside drain is characterized by the provision of maximum discharge with a given cross-sectional area. Other advantages than the hydraulic performance, for instance, for a given discharge rate, the best hydraulic section could guarantee the least cross-sectional area of the channel. Substantial savings could be made by reducing excavation and using fewer channel linings such as reinforced concrete.
Lastly, any roadside drain section selected should be large enough to permit the required discharge, as deep as required to provide a satisfactory outlet for both surface and subsurface drainage needs of the area served, and of a width-depth ratio and side slopes which will result in a stable channel which can be maintained in a satisfactory condition at a reasonable cost.
Reference(s)
King, H. W. and Brater, E. F. (1963). Handbook of Hydraulics, Fifth Edition. McGraw-Hill Book Company, Inc,, New York.