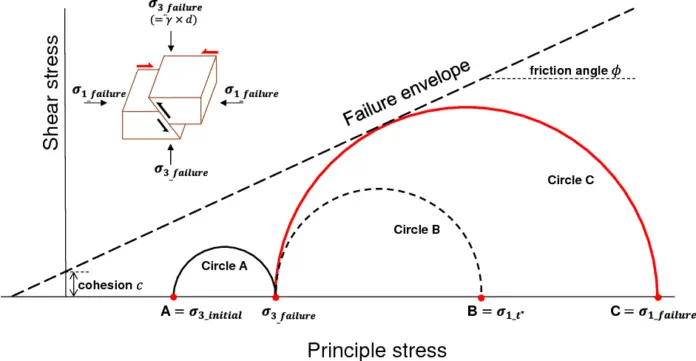
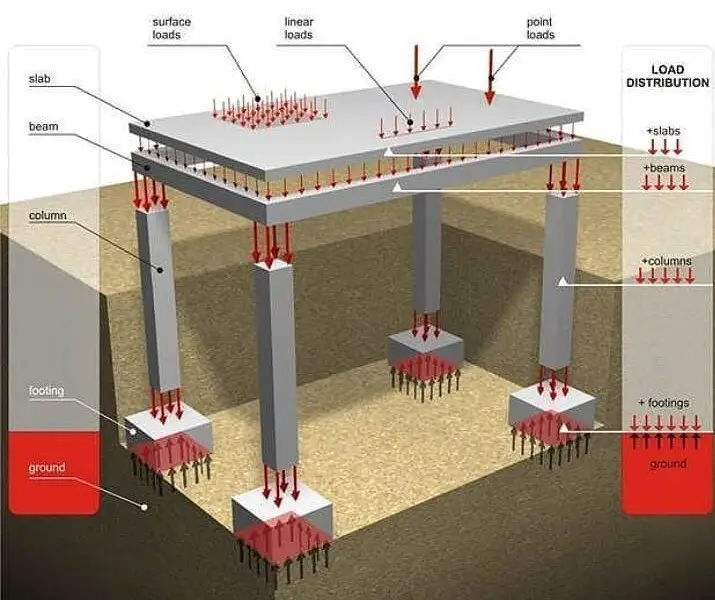
Live loads are loads produced from the use and occupancy of a building. They include the loads from human occupancy, furniture, vehicles, anticipated rare events such as the gathering of people and stacking of materials, moveable machines and equipment, storage, maintenance activities, etc. The values of live load for each type of building are usually defined by the codes of practice, and that is why the use of any structure must be defined before the design is commenced.
Live loads on floors of buildings are defined by a uniformly distributed load, line load, and concentrated load, which, however, must not be applied simultaneously. The uniformly distributed load is used for all global verifications and general designs, while the concentrated load is usually adopted for local verifications. Floor loadings which are made up of live loads and dead loads are combined for the design of slabs and floors.
Live loads are measured in pounds per square foot (psf) in the United States of America, while they are typically measured in kilo Newtons per square meter (kN/m2) in the UK and much of Europe. Sometimes, environmental loads, such as wind loads, are treated separately from live loads.
According to EN 1991-1-1:2002, imposed loads should be taken into account as quasi-static actions. However, dynamic effects may be included in the load models if there is no risk of resonance or other significant dynamic response from the structure. If resonance effects from the synchronised rhythmic movement of people or dancing or jumping may be expected, the load model should be determined for special dynamic analysis.

Categories of Buildings
To determine the imposed loads, floor and roof areas in buildings should be subdivided into categories according to their use (see Table 1). Areas in residential, social, commercial and administrative buildings shall be divided into categories according to their specific uses shown in Table 6.1 of EN 1991-1-1:2002.
| Category | Specific Use | Example |
| A | Areas for domestic and residential activities | Rooms in residential buildings and houses; bedrooms and wards in hospitals; bedrooms in hotels and hostels kitchens and toilets. |
| B | Office areas | |
| C | Areas where people may congregate (with the exception of areas defined under categories A, B, and D. | C1: Areas with tables, etc. e.g. areas in schools, cafés, restaurants, dining halls, reading rooms, and receptions. C2: Areas with fixed seats, e.g. areas in churches, theatres or cinemas, conference rooms, lecture halls, assembly halls, waiting rooms, and railway waiting rooms. C3: Areas without obstacles for moving people, e g. areas in museums, exhibition rooms, etc. and access areas in public and administration buildings, hotels, hospitals, and railway station forecourts. C4: Areas with possible physical activities, e.g. dance malls, gymnastic rooms, and stages. C5: Areas susceptible to large crowds, e.g. in buildings for public events like concert halls, sports halls including stands, terraces and access areas and railway platforms. |
| D | Shopping areas | D1: Areas in general retail shops D2: Areas in department stores |
| E | Storage areas | E1: Areas susceptible to accumulation of goods, including access areas E2: Industrial areas |
Live Load Values for Different Categories of Buildings
The values of live loads for category A buildings (areas for domestic and residential activities) are provided in Table 2.
| Sub-category | Example | qk (kN/m2) | Qk (kN) |
| A1 | All usages within self-contained dwelling units (a unit occupied by a single family or a modular student accommodation unit with a secure door and comprising not more than six single bedrooms and an internal corridor) Communal areas (including kitchens) in blocks of flats with limited use (see Note 1). For communal areas in other blocks of flats, see A5, A6 and C3 | 1.5 | 2.0 |
| A2 | Bedrooms and dormitories except those in self-contained single-family dwelling units and in hotels and motels | 1.5 | 2.0 |
| A3 | Bedrooms in hotels and motels; hospital wards; toilet areas | 2.0 | 2.0 |
| A4 | Billiard/snooker rooms | 2.0 | 2.7 |
| A5 | Balconies in single-family dwelling units and communal areas in blocks of flats with limited use (see Note 1) | 2.5 | 2.0 |
| A6 | Balconies in hostels, guest houses, residential clubs and communal areas in blocks of flats except those covered by Note 1 | Same as the rooms to which they give access but with a minimum of 3.0 | 2.0 (concentrated at the outer edge) |
| A7 | Balconies in hotels and motels | Same as the rooms to which they give access but with a minimum of 4.0 | 2.0 (concentrated at the outer edge) |

The values of live loads for category B buildings (office areas) are provided in Table 3;
| Sub-category | Example | qk (kN/m2) | Qk (kN) |
| B1 | General use other than in B2 | 2.5 | 2.7 |
| B2 | At or below ground floor level | 3.0 | 2.7 |

The values of live loads for category C buildings (areas where people may congregate) are provided in Table 4;
| Sub-category | Example | qk (kN/m2) | Qk (kN) | |
| C1 | Areas with tables | 2.0 – 3.0 | 3.0 – 4.0 | |
| C11 | Public, institutional and communal dining rooms and lounges, cafes and restaurants (see Note 2) | 2.0 | 3.0 | |
| C12 | Reading rooms with no book storage | 2.5 | 4.0 | |
| C13 | Classrooms | 3.0 | 3.6 | |
| C2 | Areas with fixed seats | 3.0 – 4.0 | 2.5 – 7.0 | |
| C21 | Assembly areas with fixed seating (see Note 3) | 4.0 | 3.6 | |
| C22 | Places of worship | 3.0 | 2.7 | |
| C3 | Areas without obstacles for moving people | 3.0 – 5.0 | 4.0 – 7.0 | |
| C31 | Corridors, hallways, aisles in institutional-type buildings not subjected to crowds or wheeled vehicles, hostels, guest houses, residential clubs, and communal areas in blocks of flats not covered by Note 1 | 3.0 | 4.5 | |
| C32 | Stairs, landings in institutional-type buildings not subjected to crowds or wheeled vehicles, hostels, guest houses, residential clubs, and communal areas in blocks of flats not covered by Note 1 | 3.0 | 4.0 | |
| C33 | Corridors, hallways, aisles in all buildings not covered by C31 and C32, including hotels and motels and institutional buildings subjected to crowds | 4.0 | 4.5 | |
| C34 | Corridors, hallways, aisles in all buildings not covered by C31 and C32, including hotels and motels and institutional buildings subjected to wheeled vehicles, including trolleys | 5.0 | 4.5 | |
| C35 | Stairs, landings in all buildings not covered by C31 and C32, including hotels and motels and institutional buildings subjected to crowds | 4.0 | 4.0 | |
| C36 | Walkways – Light duty (access suitable for one person, walkway width approx 600 mm) | 3.0 | 4.5 | |
| C37 | Walkways – General duty (regular two-way pedestrian traffic) | 5.0 | 3.6 | |
| C38 | Walkways – Heavy duty (high-density pedestrian traffic including escape routes) | 7.5 | 4.5 | |
| C39 | Museum floors and art galleries for exhibition purposes | 4.0 | 4.5 | |
| C4 | Areas with possible physical activities | 4.5 – 5.0 | 3.5 – 7.0 | |
| C41 | Dance halls and studios, gymnasia, stages (see Note 5) | 5.0 | 3.6 | |
| C42 | Drill halls and drill rooms (see Note 5) | 5.0 | 7.0 | |
| C5 | Areas susceptible to large crowds | 5.0 – 7.5 | 3.5 – 4.5 | |
| C51 | Assembly areas without fixed seating, concert halls, bars and places of worship (see Note 4 and Note 5) | 5.0 | 3.6 | |
| C52 | Stages in public assembly areas (see Note 5) | 7.5 | 4.5 |

The values of live loads for category D buildings (shopping areas) are provided in Table 5;
| Sub-category | Example | qk (kN/m2) | Qk (kN) |
| D1 | Areas in general retail shops | 4.0 | 3.6 |
| D2 | Areas in department stores | 4.0 | 3.6 |
NOTE 1: Communal areas in blocks of flats with limited use are blocks of flats not more than three storeys in height and with not more than four self-contained dwelling units per floor accessible from one staircase.
NOTE 2: Where the areas described by C11 might be subjected to loads due to physical activities or overcrowding, e.g. a hotel dining room used as a dance floor, imposed loads should be based on C4 or C5 as appropriate. Reference should also be made to Note 5.
NOTE 3: Fixed seating is seating where its removal and the use of the space for other purposes is improbable.
NOTE 4: For grandstands and stadia, reference should be made to the requirements of the appropriate certifying authority.
NOTE 5: For structures that might be susceptible to resonance effects, reference should be made to NA.2.1. of NA to BS EN 1991-1-1:2002.

The values of live loads for category E buildings (storage and industrial buildings) are provided in Table 6;
| Sub-category | Examples | qk (kN/m2) | Qk (kN) |
| E11 | General areas for static equipment not specified elsewhere (institutional and public buildings) | 2.0 | 1.8 |
| E12 | Reading rooms with book storage, e.g. libraries | 4.0 | 4.5 |
| E13 | General storage other than those specified (see Note) | 2.4 per metre of the storage height | 7.0 |
| E14 | File rooms, filing and storage space (offices) | 5.0 | 4.5 |
| E15 | Stack rooms (books) | 2.4 per metre of storage height but with a minimum of 6.5 | 7.0 |
| E16 | Paper storage for printing plants and stationery stores | 4.0 per metre of the storage height | 9.0 |
| E17 | Dense mobile stacking (books) on mobile trolleys, in public and institutional buildings | 4.8 per metre of storage height but with a minimum of 9.6 | 7.0 |
| E18 | Dense mobile stacking (books) on mobile trucks, in warehouses | 4.8 per metre of storage height but with a minimum of 15.0 | 7.0 |
| E19 | Cold storage | 5.0 per metre of storage height but with a minimum of 15.0 | 9.0 |
| E2 | See PD 6688 for imposed loads on floors for areas of industrial use |
However, the recommended value for imposed load due to storage is specified as 7.5 kN/m2 in clause 6.3.2 of EN 1991-1-1:2002. The equivalent concentrated load is 7.0 kN.

For garages and vehicle traffic areas, the imposed load for vehicles weighing less than 30 kN (about 3000 kg), qk = 2.5 kN/m2, and Qk = 7.0 kN. For vehicles weighing more than 30 kN but less than 160 kN, qk = 5 kN/m2 while the concentrated load should be specially determined. The uniformly distributed load and the concentrated load should not be applied simultaneously.