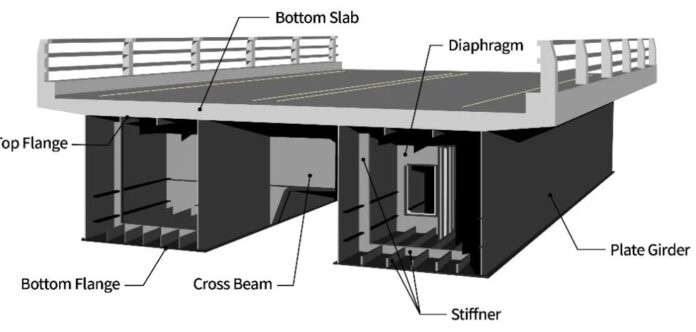
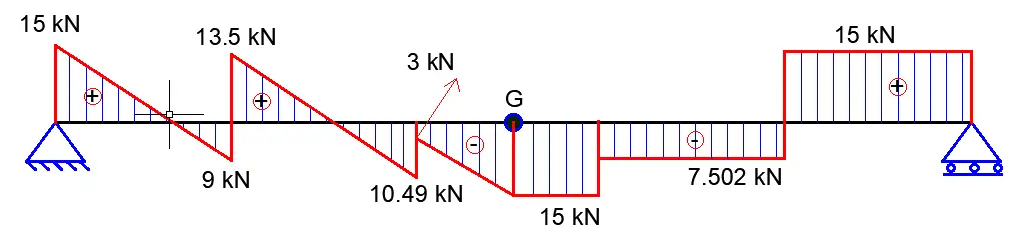
The Institution of Civil Engineers (ICE) conditions of contract in the UK allow the Engineer of a project to appoint a representative on site, typically called the Resident Engineer (RE), to oversee the construction and completion of the project (Clause 2(3)). The engineer can give the resident engineer any of their responsibilities and powers.
In this case, the Engineer refers to an independent engineer (registered engineer personnel or a consulting firm) appointed by the owners of the projects (client) to administer the contract on their behalf. Clause 2(8) of ICE conditions of contract mandates that this Engineer act impartially within the contract’s framework, considering all relevant factors. While the Engineer may be a consultant hired by the employer (client) or an internal staff member, this in no way compromises their obligation to remain unbiased in the contract administration.
As hinted in the opening paragraph of this article, the Engineer appointed by the client to administer a contract has the right to appoint a Resident Engineer who will act on his behalf on site. The resident engineer serves as an extension of the Engineer, exercising delegated powers with the same impartiality.

Therefore, the resident engineer must always follow the engineer’s guidance and only use the authority given to him. He must understand that his actions represent the engineer, and so he must consult the engineer before doing anything he is unsure about. He can offer his ideas to the engineer, identify challenges and suggest solutions; and since he is always on site, he should alert the engineer of any potential issues. When making decisions, he must know his own technical limits and leave matters that need experts to the engineer or more qualified people to decide.
This article discusses the duties and functions that are delegated to the Resident Engineer and those that are not under the ICE conditions.
Functions Delegated to the Resident Engineer
It is typical for the resident engineer’s assigned responsibilities and authorities under the ICE framework to encompass, in whole or in part, the functions listed below.
- Confirming the methods of construction details; ensuring that the contractor receives clear instructions and any necessary information on time. This means that the Resident Engineer has the power to review the construction methodology of the contractor. He also has the responsibility of providing answers and information good time to the contractor in relation to the success of the project.
- Requesting and/or ordering all materials and items that the client will supply under other contracts and that will be part of the works in advance. The Resident Engineer must always request materials ahead of time in order not to incur unnecessary delays in the project.
- Inspecting the materials and workmanship for quality and compliance; giving directions for fixing any defects.
- Verifying the lines, levels, layout, etc. of the works to match the drawings.
- Providing additional instructions, drawings and details as needed to achieve satisfactory construction of the works.
- Assessing the amount of work completed, reviewing the contractor’s interim statements and getting them ready for the engineer’s approval.
- Coordinating, supervising and performing all tests required and maintaining records of them. This may include soil tests, asphalt tests, concrete tests, steel tests, etc.
- Documenting construction progress in detail; monitoring the estimated final total cost of the project.
- Evaluating all claims from the contractor, collecting data related to such claims, and sending the contractor a preliminary reply to each claim.
- Checking daywork sheets, price increases, and all other matters that need accountancy verification.
- Inspecting the design of contractor’s temporary works for safety and quality of permanent works.
- Serving as the engineer’s Safety Supervisor on site.
- Informing the engineer of all the above in the way he wants.

Functions not Delegated to the Resident Engineer
According to the ICE conditions, there are some powers which the engineer cannot delegate to the Resident Engineer. Some of them are;
- Certifying payments and time extensions for unforeseen challenges, difficulties, or obstacles.
- Granting schedule flexibility to accommodate project needs. This means that the Resident Engineer does not have the authority to grant time extensions for project completion.
- Issuing certificates marking key project stages (substantial completion, defects corrected, final payment)
- Notifying the employer if the contractor abandons or seems unable to finish the project.
- Making rulings on disagreements before formal legal mechanisms like adjudication or arbitration.
- Issuing variation orders (VOs) or authorize payment to the contractor for delay
- Approving the contractor’s programme for construction.
- Issuing interim payment certificates;
The reason why the Resident Engineer may not be allowed to issue variation orders (VO’s) is to enable the engineer himself to scrutinize both the rationale and the financial implications of any proposed variation order (VO). Notably, for overseas projects, the resident engineer might be entrusted with the authority to issue VOs and interim payment certificates. In such situations, the resident engineer would typically have a qualified on-site team to meticulously review proposed VOs and interim payments before authorizing them.
It is important to note that the contractor will likely refuse to carry out any changes to the work that the Resident Engineer asks for unless he gets a VO from the engineer beforehand. This implies that the contractor expects to be informed of the payment for the changed work. The RE should usually be able to tell how the payment for the changed work will be done. However, the contractor has to follow the instructions and do the work as asked and the engineer will have to give a VO that specifies the payment rates as per the contract.
Extra Guides for Resident Engineers on Site
Some of the points that a Resident Engineer must watch out for on-site are as follows;
- All instructions given to the contractor must be in writing, and if given verbally, must get to them in writing ‘as soon as the situation allows’ (Clause 2(6)(b)).
- If the contractor gets a verbal instruction and writes it down, and the engineer does not disagree with it ‘immediately’, then the written confirmation is ‘considered a written instruction by the engineer’ (Clause 2(6)(b)). These written confirmations of oral instructions – or ‘CVIs’ as they are known – can cause problems for the RE.
- Even if a Resident Engineer does not have the authority to determine how much should be paid (if any) for a contractor’s request for extra payment, he can write to the contractor and express his opinion on the request. He must do this, in every case, so that the record shows his perspective on the facts.
- There are many ‘time clauses’ in the contract conditions, that is, clauses that set a deadline for the engineer (and probably the RE too) to act. A key example is the obligation that the engineer must give feedback on the contractor’s planned programme within 21 days of getting it, otherwise, the engineer is assumed to have approved it (Clause 14(2)). The same, essentially, applies to any partial programme or updated programme the contractor provides. Therefore if the engineer does not give feedback within 21 days, the contractor’s programme is assumed to be accepted and inconsistencies may arise if the programme does not match the specified timing.
- The RE must make sure that the contractor gets all the approvals, drawings, details and other information he requires to build the works, in a timely manner; otherwise, the contractor may ask for compensation for delay (Clause 7(4)).
- The RE must not allow lower quality materials or workmanship than what is specified, even if the contractor proposes a lower price than the bill price for the specified material unless the engineer consents to this. Such a change is a variation that needs a VO.
- The RE has to notify the contractor right away when he notices any flaws in materials or workmanship, because it may be very hard to fix a faulty part of the work after it is finished. Therefore quality checks should happen as soon as an activity begins, or as soon as material for the permanent works arrives at the site.