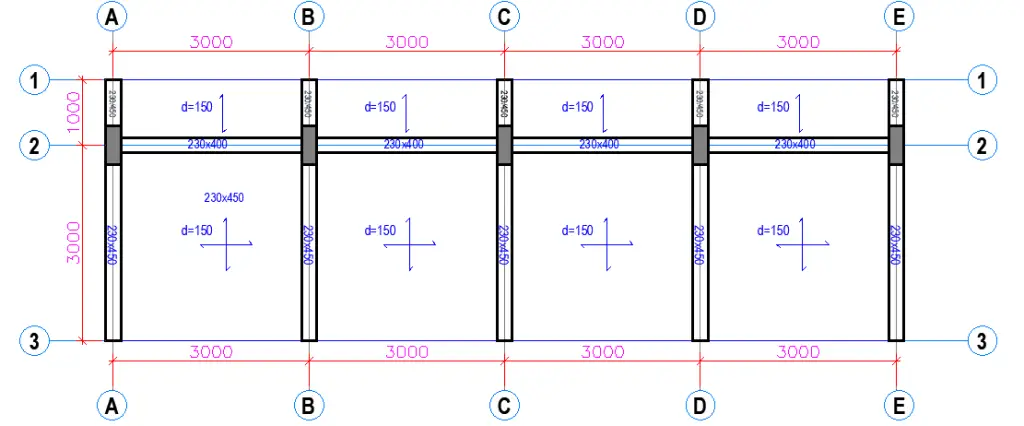
There are three basic needs of man: food, shelter and clothing. A building is another name for shelter and is therefore one of the basic needs of man. We construct buildings to provide shelter for man, animals, machines, properties and workplaces.
A building protects us, our properties and our animals from harsh environmental conditions. The building also helps to suspend us in space as in multi-storey buildings hence enabling a large number of people to occupy a small area of land. Our media space has been inundated with the news of building failures/collapse.
These have come with numerous headlines like “Five Killed, 26 rescued in Anambra building collapse[1]”, “Abuja building collapse: 4 rescued as search rescue operations end”[2], “Tears as 22 pupils killed and 120 trapped in Plateau school building collapse[3]” and the list goes on.

What is Building failure?
A building has failed if it is unable to perform its intended function. The failure of a building could be a result of many factors. It is best traced by looking into the building team. Like a football team, the construction of a building requires the input of different professionals.
Each professional like each member of a football team supplies one or more of some of the ingredients needed for the building structure to meet its intended needs. The absence or failure of which leaves the project deficient. Just like in food and nutrition classes, the deficiency points to what is lacking in the product. The addition of the ingredients/input lacking heals or restores the product.
Let’s take a look at these professionals and their inputs:
The Architect: The architect conceives the building project. He is the one with the mental picture of the building before it is built. This he puts down on paper in the form of a set of drawings. The drawings show the size, shape, look etc of the building to the nearest millimetre. He is usually regarded as the head of the building team.
The Civil/Structural Engineer: The Civil/Structural engineer studies the architectural drawings and produces the structural drawings. The structural drawings are a set of instructions (ingredients) needed to enable the building to stand firm meeting both the requirements for stability and serviceability. He must be able to understand the architectural drawings. He must understand the soil characteristics of the chosen site and the available building materials in the market.
Electrical and Mechanical Engineers: The Electrical and Mechanical engineers study the architectural drawings and produce the electrical and mechanical drawings respectively. Modern buildings come with electrical and mechanical components like lights, sockets, heaters, plumbing systems, lifts etc. Their drawings provide information on the electrical and mechanical components of the building structure to enable them to work as envisaged by the architect.
Quantity Surveyor: The quantity surveyor collects the drawings (ingredients) provided by the Architect, Civil/Structural engineers, Electrical and Mechanical engineers and works out an estimate of the resources needed to execute the project. He facilitates an estimate of the project cost.
Land Surveyor: The land surveyor helps us position the building project accurately on land as provided for in the site plan (building setting out). Hence in large building projects, they are often hired to enable the contractor to locate the exact place/point to erect the building. They are excellent at transferring geometry from paper to land. They can also be hired to position building components like columns as specified by the Civil/Structural engineers.
Town Planner: The Town planner plans our city to make it more habitable. He prepares the plan/layout of our cities to enable easy movement of people and guarantee their access to essential facilities.
The Builder: The builder is the professional trained in school to become a contractor (the Cook). He is the one who collects the instructions (ingredients) from the other professionals and sets out to execute (cook) the building project (food).
Failure types
A building fails when one or more of the inputs of any of the building teams are deficient. It will be convenient to define the failures along the lines of the deficient building professional.
Architect-deficient: This is the failure type that is ripe when the input of a professional Architect is either lacking or deficient. If the final project is smaller than expected or the rooms, storey height, flow etc are at variance with what is expected for us to put the house into good or expected use, we first look in the direction of the Architect.
He is supposed to be the person who supplied those ingredients. If the ingredients (drawings) he supplied are good and as expected, we turn to the cook (the contractor) for reasons for not adhering to the specifications (recipe) provided by the Architect.

Civil/Structural engineer-deficient: This is the failure type we see when the input of a Civil/Structural engineer is deficient or lacking. Recall that the Civil/Structural engineer is the professional trained in school to estimate loads, analyse forces and recommend the number, position, sizes and nature of the structural elements of a building project with the aim of enabling the building stand.
He is the one who provides the ingredients that ensure that the concept of the Architect can stand and withstand effectively its self-weight, imposed loads and other environmental forces expected. When offensive shear cracks are spotted, when the deflection of structural members is excessive, when high and noticeable subsidence of the building is observed or when the building collapses he is the expert to look for.
He is supposed to be the person who supplied those ingredients. If the ingredients (structural drawings) he supplied are good and as expected, we turn to the cook (the contractor) to give us reasons for not adhering to the specifications (recipe) provided by the Civil/Structural engineers.
The Electrical and Mechanical engineer-deficient: If the final product has electrical fittings that are poorly located, electrical components that are not working properly or mechanical and plumbing systems that refuse to work properly, we first look in the direction of the electrical and mechanical engineers.
They are supposed to supply those ingredients. If the ingredients (drawings) they supplied are good and as expected, we turn to the cook (the contractor) for reasons for not adhering to the specifications (recipe) provided by the electrical and mechanical engineers.

Quantity surveyor-deficient: If after allocation of the resources/quantities (ingredients) he specified and the project is uncompleted, we first look in his direction to ascertain if what he estimated is correct. If they are correct we turn to the cook (the contractor) for an explanation.
The land surveyor-deficient: If after execution we notice that the position or orientation of the building is not as expected we first look at the site plan, if the specifications of the site plan are good we then turn in the direction of the land surveyor for reasons for not adhering to specifications in the site plan.
The Town planner-deficient: If we see buildings that are jam-packed, have inadequate setbacks, or sited in awkward places (like a factory at the centre of a high-density residential area) we first look in the direction of the Town planner. We check if the site plan got the approval of the Town planner in the regulatory agency. If the plan is good and is approved we turn to the contractor to give us reasons why he refused to adhere to the instructions in the site plan.
The Builder-deficient: If the structure is not deficient in any way in the specifications from the other building professionals after a vetting process is done, the Builder is first held responsible for any failure observed in the building.
Our building construction industry is still like a student who is not bothered about what he scores in an exam. He is happy to score anything from 2% to 100%. He is only bothered when he scores 0%. Sure 0% is a failure. But failure actually starts from 39% and below.
A building that is wrongly sited is a failure. A building that offers poor circulation/movement within the building is a failure. A building that is poorly ventilated or poorly lit is a failure. A building that could not be completed after the release of the estimated cost is a failure. A building that has no functional safety features is a failure. In each of these cases the building scores below 39%. But we usually react only when the building collapses that is when it scored 0%. Well, that too is a failure.
Building Collapse
We can see that a building collapses when the inputs of a Civil/Structural engineer are lacking. A building collapses if the recommendations of the Civil/Structural engineer are not there or are poorly adhered to. Building collapse is the worst form of building failure. It is the failure which once it occurs cannot be remedied.
When a building collapses, the building dies and another must be built to replace the collapsed one. This is the reason why building collapse generates the most public attention. This consequently places a high value on the civil engineer hence the reason why almost everybody wants to be called an engineer in the construction site.

Causes of Building collapse
To understand the causes of building collapse we need to throw more light on the inputs of a Civil/Structural engineer, the materials he/she uses and the implementation of his/her recommendations.
(a) Structural Design Error
A building can collapse as a result of a faulty Structural design. The Civil/Structural engineer designs the building against collapse. This he/she does by the provision of a set of instructions. These instructions are presented in the form of some drawings known as structural drawings. When these instructions are not correct we have a design error.
Causes of Design Error
- Use of Quacks: It is common knowledge that many people who parade themselves as engineers are not engineers. They have not passed through the walls of a university to study engineering. They are also not licensed by COREN to practice and be called engineers. These quacks occasionally produce structural drawings for non-suspecting and ignorant clients. Because of their deficit in civil engineering knowledge, their design often is fraught with design errors.
- Incompetent engineers: Not all engineers are competent. The learning curve of most Civil/Structural engineers does not end at the university. It continues during professional practice and often throughout their working career. A Structural design error can occur when such an engineer is asked to produce a structural design. You simply cannot give what you do not have.
- An Engineer’s mistake: Though very rare a sound engineer can make mistakes in his design. This can be a result of human error, fatigue etc. The error can be transferred to the structural drawings.
- A Draughtsman’s error: The engineering design is communicated in the form of a set of drawings. These drawings are usually produced by the engineering draughtsman from the design calculations of the engineer. If the draughtsman makes a human error it will translate to a design error as the structural drawings which are his final drawings will have an error.
(b) Material Error: The Civil/Structural engineer in the preparation of his design calculations makes use of some parameters. These parameters are the properties of the materials to be used in constructing the proposed building. He recommends a reinforcement steel (iron rod) of a particular property. He recommends concrete of a particular property.
He assumes the building is to rest on the soil strata of a particular property (this information he obtains from a soil investigation carried out by a Civil/Geotechnical Engineer). The structural design he/she produces is based on these parameters. It is therefore necessary to ensure that only materials of the recommended properties are used.
Any material with a property unfavourable to what was assumed by the designer is sub-standard and can lead to a building collapse. The common materials are cement, fine aggregates, coarse aggregate, reinforcement rods and water.
(c) Implementation Error: Here comes the error from the contractor (the cook). He is supposed to be able to understand the recommendations of the civil/structural engineer as presented in the structural drawings. If he fails to understand the drawings and the recommended materials or deliberately flouts the instructions there will be an implementation error. This implementation error is one of the most common causes of building collapse.
(d) Poor Building Regulation: These are the processes for regulating and monitoring the pre-construction, construction and post-construction activities of buildings. Human activities are often motivated by personal gains hence the need to regulate them to ensure that the correct things are done. These are supposed to be done by our Building regulatory agencies.
Our regulatory agencies are supposed to vet all the drawings to be used for the execution of a building, ensure that competent hands are involved in the execution of building projects and also monitor the execution to ensure that only materials of the desired qualities as recommended in the structural drawings are used.
The work is huge. Our regulatory agencies are often made up of personnel who lack both the required expertise and numerical numbers for such an enormous task. Many buildings go on in our premised unnoticed by these agencies hence the incessant building collapse.
Solutions and Recommendations
(1) Synergy with the building industry professional associations: Synergy with the professional associations will release to the regulatory agencies a pool of ready and viable hands for effective building regulation. The agency will tap from their expertise and numerical strength. They (the professionals) being one of the ultimate beneficiaries of a well-regulated industry will be willing to assist the regulatory agencies.
This can be done through the strengthening of the Building Control departments in the Building regulation Agencies. These departments should have an Engineering Unit, Architectural Unit and Town planning Unit. These Units should be manned by professionals from the respective professional organizations both on a full-time and part-time basis. Each approval must pass through and be cleared by these Units for thorough vetting and adequate documentation. Each building must have the seals of approval of these Units on their approved drawings.
Professional organizations are blessed with numbers and expertise and can do this as their contribution to curbing building failures. This will save the government a lot of resources as they may never be able to employ enough trained hands to do this work. The regulation from these bodies will be more effective as they know their members and are also equipped by law to deal with them when they err.
This will deal a final blow on quackery in the Industry and also ensure that adequate, good and accessible records on every building are kept. It will provide no hiding place for quacks or any fraudulent professional. The government finally will be able to put its blame on these organizations when there is a failure.
(2) De-zoning of Regulatory Agencies: Building approvals and monitoring should be made more efficient and effective by de-zoning the regulatory agencies. There should be a branch of every Regulatory agency in every local government area in the state and each branch should be a microcosm of the main branch.
This means that these branches will have their respective building control departments and should be able to approve and monitor buildings. This will bring building control and regulation closer to the location of the construction site and make them more effective. Most logistics and bottlenecks that breed corruption and compromise are removed. It will then be very easy to pin down failures to erring officers and offices.
(3) The relevant professional should be the contractor (cook): As painful as this may sound the cook (the person who interprets the instructions of the other professionals with the aim of producing the finished product) should be a professional who can interpret the instructions from the Architect and Civil/Structural engineer.
A threatening danger faced by the construction industry is the lack of regulation on who should be the contractor. In our construction industry, the contractor can be anybody. He needs not know how to interpret the information supplied by the other professionals. He needs not know the consequences of flouting their instructions. He only needs gut and the ability to imitate what a professional elsewhere did to be a contractor. This leaves our regulatory agencies stretched to their limits.
Building collapse will remain until we begin to regulate who executes building projects and if possible criminalize the execution of building projects by non-building professionals. Building professionals are people who by training are equipped to interpret the instructions from the other professionals.
The architect has a smattering knowledge of structures, quantities etc to be able to work effectively in a building team. The civil engineer is taught the very rudiments of architecture to enable him to interpret the drawing and hence recommend the appropriate structural elements. This also applies to the Builder. Building construction must be executed by a person who can interpret appropriately the instructions from other professionals. This applies to other building professionals.
(4) Sub-standard materials: We may have noticed my silence on the presence of sub-standard materials in our market. This is deliberate. Sub-standard materials are in our market because of the predominance of bad contractors. In our food market, bad or poorly prepared ingredients that do not give a tasty dish do not last in our market. Why? Because Nigerian women are good cooks, they spot the bad ingredients, notice their damaging effect on their food and simply refuse to patronize them.
The consequence is that the bad ingredient soon disappears. Just imagine if we wake up one day and discover that all the good Nigerian cooks have disappeared. What do you think will happen to bad ingredients in the market? They will strive. The bad cooks (remaining) will use them to produce food that is of poorer quality and will not even know why their food is not tasty. This is the reason why combating substandard reinforcement bars, the use of very weak concrete and aggregates for structural elements etc are still a challenge in our environment.
(5) Imposition of penalties for defaulters: This cannot be overemphasized. The imposition of penalties for defaulters will also serve as a deterrent. The Regulatory Agencies must also be liable for the collapse of any building they approve. It is their responsibility to ensure that competent, reachable and verifiable professionals are attached to each building project. They can introduce more instruments and forms to ensure this.
Engr. Odinaka Victor Okonkwo (Ph.D)
Department of Civil Engineering, Nnamdi Azikiwe University, Awka, Nigeria.
Past Chairman, Nigerian Society of Engineers (NSE) Awka Branch.
E-mail: vo.okonkwo@unizik.edu.ng
Sources and Citations
[1] https://www.premiumtimesng.com/news/more-news/672382-five-killed-26-rescued-in-anambra-building-collapse.html?tztc=1
[2] https://www.9jabrief.com/view_feed?feed_key=24739
[3] https://punchng.com/tears-as-22-pupils-killed-120-trapped-in-plateau-school-building-collapse/